梯形模糊层次分析法的数学实验教学质量评价方法

王正萍，许庆兵

(滁州职业技术学院，安徽滁州239000)

0 引言

近年来，随着我国高等教育“大众化”趋势的发展，我国高等职业教育招生人数逐年增加，但经过层层筛选，最后批次录取的学生入学起点相对较低(2011年和2012年安徽省高职最低录取线文理科均为200分)，所招的学生成绩普遍不高.并且很多工科专业都是文理生兼收，学生的数学基础知识普遍较薄弱.2012年，部分高职院校开始实行自主招生，招生范围扩展为中专、中技学生，这也给高职高等数学教学带来了很大的挑战.传统的高等数学教学模式传递的信息量小，学生兴趣不高，教学效率低，已经不能适应新形势下的高职高等数学教学，所以现有的高等数学教学模式亟待改革.数学实验课是在上世纪80年代末产生于美国的一些大学，它通过结合使用计算机的实验，引导学生进入数学的世界.我国高校在上世纪90年代中后期开始设置“数学实验”课，其发展也极为迅速，目前许多本科院校已经开设这门课.随着教学改革的不断深入，“数学实验”课已成为当前工科数学教学改革探索的一个重要方向.然而，由于种种原因，在我国的高职院校里，这门课程很少开设，关于高职数学实验课教学实践方面的研究也就更少了.为进一步发挥数学学科在培养学生实践与创新能力方面的教育功能，探索出既符合高等教育改革发展需求的，又适合高职院校实际情况的数学教学改革新举措，结合近几年实验课教学开展的实际情况，在充分调查、研究、学习的基础上，本着学以致用为中心的新型教育观和人才观理念，展开对高职院校数学实验课教学质量评价方法研究，建立一个高职院校数学实验课教学评价模型，客观地评价该课程的教学质量，分析出影响教学效果的重要因素，以促进高职院校高等数学实验课的教学改革.

1 高职院校高等数学实验课教学质量评价模型的构建

通常，有关教学质量方面的评价多采用层次分析法(Analytic Hierarchy Process，简称AHP)，具体的相关研究成果可以参见[1-8].AHP方法是由美国T.L.Saaty教授于上世纪70年代提出的一种定性和定量结合的、系统化、层次化的分析方法[7].层次分析法的一个重要步骤需要构造判断矩阵，然后对评价体系中的两每个指标进行比较并采用简单的1～9标度法进行赋值.由于在对实际问题描述时，往往会遇到不清晰，无法简单地进行描述的情况，因而，传统层次分析法中1～9标度法不能确切反映出专家的实际评判结果，于是就有可能造成判断结果的不准确.为了准确、客观地地反映评判结果，采用梯形模糊数的层次分析法判断标度(表1)，对各级指标中两两间进行比较、赋值，并采用梯形模糊数层次分析法(Trapezium Fuzzy AHP，简称TF-AHP)，对高职院校数学实验课教学质量进行赋权，然后用模糊综合评判法建立教学质量评价模型.

表1 梯形模糊数的层次分析法判断标度

1.1 高职院校高等数学实验课教学质量评价指标体系的设定

合理的评价指标体系是对《高等数学》实验教学质量评价进行有效评价的前提和基础.依据《高等数学》实验教学培养目标中的要求建立以实验教师队伍、实验条件、实验教学过程、实验教学效果4个一级指标在内的包括职称结构、专业技术水平、教师考核、实验内容、实验手段、实验难度、学生实验成绩、学习数学兴趣、运用数学软件能力、实验设备与环境以及实验室管理制度等11个二级指标的二层次的评价指标体系(见表2)，其中各单要素的子集Bi(i=1，2，3，4)分别为B1=(C11，C12，C13)，B2=(C21，C22，C23)，B3=(C31，C32，C33)，B4=(C41，C42)，即评价要素的集合为U=(B1，B2，B3，B4).

表2 《高等数学》实验教学质量评价指标体系

1.2 评语集的设置

根据实际需要，设置的评价等级为“优”、“良”、“中”、“差”和“劣”五个等级.即评语集合为V=(v1，v2，v3，v4，v5)=(“优”，“良”，“中”，“差”，“劣”).

1.3 权重的确定

采用梯形模糊数的层次分析法确定《高等数学》实验教学质量各级评价指标权重，具体步骤如下:

1.3.1 构造梯形模糊判断矩阵

从层次结构模型的第二层开始，对于从属于或影响上一层的每个因素的同一层诸因素，用成对比较法和梯形模糊数的层次分析法判断标度构造模糊判断矩阵[8]，直到最下层.

1.3.2 一致性检验

对于梯形模糊数，最能代表其特征的为该模糊数所表示的梯形的重心[6].因而，求模糊数的梯形重心，使其清晰化是进行一致性判断时所必须要做的步骤.通过重心计算公式:

将梯形矩阵中的所有梯形数A=(a，b，c，d)变换后就可以得到普通判断矩阵，对于得到的每一个普通判断矩阵，用文献[9]中的方法做一致性检验.

1.3.3 权重求解及层次单排序

求解模糊权重的具体步骤如下:

第1步:综合专家评分意见，根据公式

求出模糊判断矩阵rij(i，j∈N).

第2步:由公式

求得各指标的模糊评价值，其中(i，j∈N).

第3步:根据梯形模糊数的期望公式，则各指标的模糊评价期望为[8]

第4步:对上式归一化处理，求得各指标的权重:

1.3.4 计算综合评价结果

1.4 评判的实施

1.4.1 求评判矩阵

将专家组(n人)依据评语级对各级指标投票的结果进行归一化处理，得单因素的隶属度(n1/n，n2/n，n3/n，n4/n，n5/n)，其中n1、n2、n3、n4、n5为该指标评为v1、v2、v3、v4、v5各等级的人数，这样便可得到各子集Bi(i=1，2，3，4)中各单要素的评判矩阵Ri(i=1，2，3，4).

1.4.2 求A中各子集评价矩阵

1.4.3 求出评价结果

1.5 《高等数学》实验教学质量教学效果的模糊综合评价

1.5.1 二级评判:

1.5.2 一级评判:

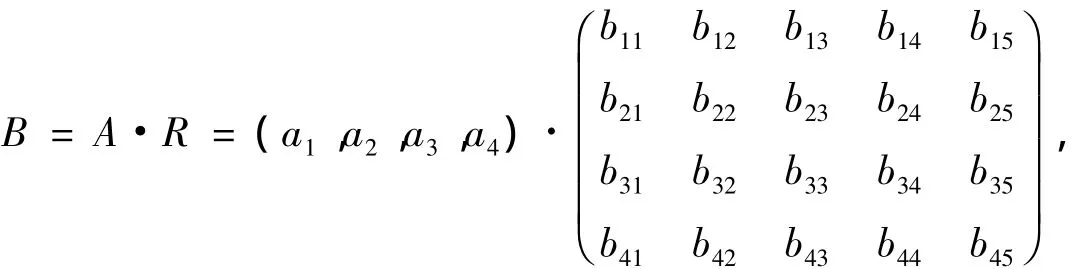
归一化得:B=(b1，b2，b3，b4，b5)，然后，依据最大隶属度原则[3]，确定《高等数学》实验教学质量评价优劣状况.

2 实例应用

2.1 构造梯形模糊判断矩阵

由于篇幅原因，这里仅以一级指标(实验教师队伍、实验条件、实验教学过程、实验教学效果)为例，说明权重的确定过程.为此，我们邀请5位专家对滁州职业技术学院《高等数学》实验教学质量给出梯形模糊判断矩阵rU－B，采用加权平均数得到综合模糊判断矩阵rU－B=

这里仅以rU－B矩阵为例，对其进行一致性检验、模糊权重求解及层次单排序.

2.2 一致性检验

利用公式(1)求出普通判断矩阵

用文献[9]求得最大特征根λmax=4.0302，一致性指标CI=(λmax－n)/(n－1)=0.0101，根据RI的数值表，查得RI=0.9，故有CR=CI/RI=0.0112＜0.1，所以，该矩阵通过一致性检验.

2.3 模糊权重计算及层次单排序

根据公式(2)求得模糊评价值如下:

同理求得

再由公式(3)求得各指标模糊评价的期望

最后根据公式(3)归一化处理，可得各指标的权重依次为:易见，w1＞w2＞w3＞w4.

2.4 计算综合评价结果

各单要素在层次总排序中综合评价计算结果，参见表1括号中数值.

2.5 评价的实施

采用2.5中的求解方法，本例的具体计算过程为:

这样，便得到专家组对实验教师队伍指标的综合评价为:

归一化有B1=(0.154，0.214，0.214，0.214，0.154).

同理可得，对实验条件、实验教学过程以及实验教学效果指标的综合评判为:

最后，得到对滁州职业技术学院《高等数学》实验教学质量的综合评价为:

3 结论

由上述计算可知，滁州职业技术学院《高等数学》实验教学质量为“优”、“良”、“中”、“差”、“劣”的隶属度分别为0.157、0.242、0.228及0.187，而0.242是这5个隶属度中最大的数值，根据最大隶属度原则，滁州职业技术学院《高等数学》实验教学质量可评为“良”等级，这一结果与实际情况基本一致.

[1] 田劲松，过家春.基于可拓学的高校教师教学质量评价[J].现代远程教育研究，2012，19(5):85-89.

[2] 董九英.高校教师教学质量评估的区间数方法[J].计算机工程与应用，2010，46(17):246-248.

[3] 王学戏.模糊综合评判在高校教师教学质量评价中的应用[J].太原师范学院学报:自然科学版，2008，28(4):50-54.

[4] 杨珍，牟占军.基于层次分析法的高校教师教学质量评价研究[J].内蒙古工业大学学报:社会科学版，2010，19(1):111-116.

[5] 朱从书.高校教师教学质量学生评估模型的实证研究[J].长江大学学报:社会科学版，2009，32(4):96-99.

[6] Lipovetsky S，Conldin M.Robust estimation of priorities in the AHP[J].European Journal of Operational Research，2002，137:110-122.

[7] Saaty T L.层次分析法[M].北京:煤炭工业出版社，1988.

[8] 王力，刘家琦.梯形模糊AHP及其在卫星方案中的应用[J].哈尔滨工业大学学报，2002，6(3):315-3l9.

[9] 姜启源.数学模型[M].北京:高等教育出版社，1987.

[10] 王芳.书籍装帧设计水平的综合评价[J].洛阳师范学院学报，2011，28(3):16-l9.