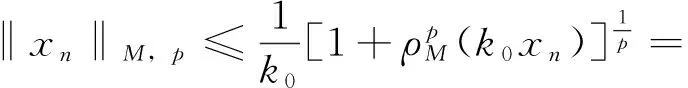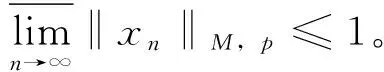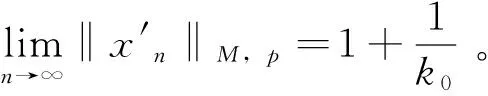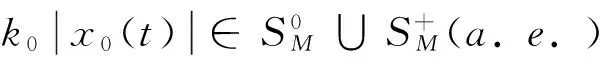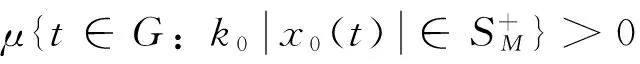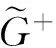赋广义Orlicz范数的Orlicz函数空间的UR点和WUR点*

段丽芬, 左明霞，王宏志

(1.通化师范学院数学学院,吉林 通化 134002;2. 哈尔滨理工大学应用科学学院, 黑龙江 哈尔滨 150080)

自Orlicz空间引入以来，其理论得到了迅速发展[1-3]，应用范围逐渐扩大[4-7]。但对赋广义Orlicz范数的Orlicz空间几何理论,我们还了解甚少。一致凸(UR)点和弱一致凸(WUR)点是Banach空间几何学的重要概念，它们在逼近论、控制论、不动点等分支中都有广泛应用[8-11]。本文给出由N-函数生成赋广义Orlicz范数的Orlicz函数空间中UR点和WUR点的判据，并据此获得了Orlicz函数空间局部一致凸和弱局部一致凸的条件。

1 定义及符号

设X是一个Banach空间,S(X)表示X的单位球面。

若Banach空间单位球面上每一点都是UR点，则称X是局部一致凸的。

设M(u),N(v)是一对互余的N-函数，p+(u)表示M(u)的右导数。M∈Δ2指如存在常数k≥2和x0>0，当|x|≥x0时，满足M(2x)≤kM(x).M∈▽2⟺N∈Δ2。记

SM={u∈R+:∀ε>0,2M(u)<

M(u+ε)+M(u-ε)}，

∃λ>0,ρM(λx)<∞}

及其闭子空间

∀λ>0,ρM(λx)<∞}

关于Orlicz范数

Luxemburg范数

‖x‖M=inf{λ>0:ρM(x/λ)≤1}

及广义Orlicz范数：

2 主要结果

定理1 设M是N--函数，p+(u)连续，x0∈S(LM,p)(1

(i)x0是UR点；

(ii)x0是WUR点；

证明(i)⟹(ii)显然。(ii)⟹(iii)分三步完成。

① 证明M∈Δ2。若不然,设z(t)∈LM,pEM,p,则有奇异泛函φ,φ(z)≠0。取D>0，使G′={t∈G:|x0(t)|≤D}具有正测度。记Gn={t∈G′:|z(t)|>n}，则μGn→0(n→∞)。令

则

n=1,2,…，则yn(t)→y0(t)(a.e.,n→∞)，从而‖yn‖N,q→‖y0‖N,q=1。由于

2≥‖x0+xn‖M,p≥

则

故

又

则

但x0≠x′，这与x0是WUR点矛盾。

不妨设x0(t)≥0(t∈G)。记

则文献[14]同样方法可证knxn(t)-k0x0(t)→0(a.e.t∈G0)(必要时取子列)。下面证明knxn(t)-k0x0(t)→0(a.e.t∈G+)。

μ{t∈G+:knxn(t)≤k0x0(t)-σ}→0(n→∞)

故

其中γ>0。因M∈Δ2，p(u)连续，有

由定理1立即可得

定理2 设M是N--函数，p+(u)连续，则对任何1

(i)LM,p局部一致凸；

(ii)LM,p弱局部一致凸；

(iii)M∈Δ2∩▽2且M(u)严格凸。

[1] RAO M M,REN Z D. Theory of Orlicz spaces[M]. New York: Mercel Dekker,1991.

[2] 刘艳丽. Orlicz空间及其对偶空间的若干几何性质[D].哈尔滨:哈尔滨理工大学, 2010.

[3] 刘春燕.广义Orlicz空间的暴露点、一致Noncreacy性质及光滑性[D].上海:上海大学, 2011.

[4] 石忠锐,翟佳羽.赋Luxemburg范数的广义Orlicz函数空间中的λ点和λ性质[J]. 华东师范大学学报：自然科学学报, 2012(1):63-73.

[5] WANG X L, HUO R, WU G. On approximation by reciprocals of polynomials with positive coefficients in Orlicz spaces [J]. Analysis in Theory and Applications, 2008, 24(4):364-379.

[6] LIANG Y Y,YANG D C,YANG S B. Applicztions of Orlicz-Hardy spaces associated with operators satisfying Posson estimates [J].Science China：Mathematics, 2011,54(11):2395-2426.

[7] 顾春贺,吴嘎日迪. Orlicz空间中三角多项式倒数对周期可微函数的逼近定理[J]. 应用泛函分析学报, 2012,12(2):180-185.

[8] 张晓华,任必军. 集值非扩张映射不动点存在与收敛性[J].河南师范大学学报:自然科学版,2009, 37(2):141-142.

[9] 高兴慧,周海云.Banach空间中关于变分不等式的收缩投影方法[J]. 工程数学学报,2011, 28(3): 406-411.

[10] 武利猛,杨军,陆海波,等. 时标上三阶非线性P-Laplacian三点边值问题的正解[J].中山大学学报:自然科学版, 2011,50(3):17-21.

[11] 陈利国,罗成,王君. 局部凸空间的中点局部k-一致凸性与中点局部k-一致光滑性[J]. 中山大学学报:自然科学版,2013,52(2):52-56.

[12] DIESTEL J. Geometry of Banach spaces [J]. Berlin:Springer Verlag,1975.

[13] 段丽芬. Orlicz空间和商空间的若干几何性质[D].哈尔滨:哈尔滨理工大学, 2004.

[14] 李小彦. 赋p-Amemiya范数Orlicz空间的若干性质[D]. 哈尔滨：哈尔滨理工大学, 2010.

[15] 陈述涛,王廷辅. Orlicz空间的UR点和WUR点[J]. 哈尔滨师范大学：自然科学学报,1992,8(3):5-10.