一种基于分块DCT变换的三维网格模型半脆弱水印算法*

徐 涛，罗中良，陈志芳，蔡彬滔

(惠州学院计算机科学系，广东 惠州 516007)

数字水印技术为多媒体信息安全领域的一个研究热点方向，在图像水印方面已有不少专家学者进行了研究探讨[1-3]，近年来该技术开始推广到三维网格模型领域[4-6]，而脆弱水印技术则为三维网格模型数字水印领域的一个新的研究重点方向。网格模型脆弱水印可分为完全脆弱水印和半脆弱水印两类。前者可以检测出任何对网格数据进行的破坏，而后者则允许水印可抵抗一定程度的非恶意数据破坏。在完全脆弱数字水印方法研究方面，Yeung等[7]提出了三维网格模型的首个脆弱水印算法，通过调整索引表中的顶点为“有效”或“无效”来嵌入水印，对网格非法篡改具有较高的敏感性，但篡改定位只能反映在抽象的二维平面映射图中；Chou等[8]在直角坐标中选中一批标记顶点(Mark Vertex)让它们与其邻域顶点之间维持一种预定义的约定关系来实现水印嵌入，具有较高的篡改敏感性，但对于篡改的位置只能给出一组可疑顶点的输出序列。而在半脆弱数字水印方法方面，Wu等[9]提出的半脆弱水印算法将顶点与一环邻域质心的矢量长度值选作水印嵌入对象，可容忍RST相似变换处理，对于篡改位置算法能给出可视化定位标识；Cho等[10]提出的算法将原始网格分解为粗糙网格和一组小波系数，将选中的一幅标志图像(Logo Pattern)作为半脆弱水印嵌入到粗糙网格中，可容忍RST相似变换处理，篡改定位只能反映在标志图像的改动上，缺乏直观性；Lin等[11]对Yeung的算法做出了改进，扩大了顶点的容忍改动范围，可容忍网格顶点坐标值量化处理，但对RST相似变换缺乏容忍能力；Chou等[12]提出的算法将半脆弱水印嵌入到模型面片的子集中，使它们与邻接的顶点保持预先定义的关系，只能容忍模型的RST相似变换。

由于半脆弱水印能够对恶意数据破坏和正常数据处理加以区分，因此具有更广泛的应用范围，而现阶段对网格模型半脆弱水印方法研究偏少。本文提出一种基于新的三维网格模型半脆弱水印算法，可定位出模型的被篡改位置。

1 网格模型半脆弱水印算法设计要求

如何正确区分来自侵权者的恶意攻击和来自用户方的正常数据处理成为算法设计的一个必要前提条件，从目前三维网格模型的应用情况来看，至少以下几种数据处理应当视为非恶意攻击：RST相似变换，包括模型的平移、旋转和各向一致缩放处理，它们不会对模型的外观视觉质量造成影响；低强度的顶点坐标值量化处理，为了节省网络带宽，可采用取整量化方法适当降低顶点坐标的浮点数精度，不应视为恶意攻击；低强度的噪声污染，模型经由网络传播复制过程中，几何数据可能会造成轻微噪声污染。但应当指出的是，顶点坐标值量化处理和噪声的强度应控制在模型“内容保持”的范围内，超出许可尺度时则应视为恶意攻击。

2 半脆弱水印嵌入算法描述

模型的旋转极易造成水印提取时出现不同步，因此本文采用了主元分析对网格模型进行校准预处理；另一方面，对于半脆弱水印来讲，需要将水印信号均匀、完整的覆盖到整个模型，因此算法要对模型进行均匀分块处理，每个分块用于隐藏一位半脆弱水印信号。

2.1 网格模型PCA校准和分割预处理

主元分析(Principal component analysis，简称为PCA)用于模型的校准定位预处理，其过程可描述如下：首先求出网格模型M的质心Vc，将质心位置设为三维笛卡尔直角坐标系的原点，对顶点坐标进行修正预处理，然后计算模型顶点的协方差矩阵，然后构造旋转矩阵R，对顶点集V中的各顶点进行坐标变换，得到姿态调整后的顶点集Vr和网格模型Mr。通过对网格模型做主元分析预处理，可有效的解决网格旋转带来的影响，在三维网格模型数据检索领域有着广泛应用[13]，在三维网格模型数字水印领域亦可以用来解决水印的同步性问题，即不论是对原始模型嵌入水印，还是对待测的疑似篡改模型提取水印，都要首先对其进行主元分析预处理，将模型调整为同一姿态，这样可使得水印信号被同步嵌入和提取。

为了使半脆弱水印可以均匀的覆盖到模型的各个部位，需要将模型按顶点的拓扑连通关系均匀分割成若干分块，这里我们采用了Metis软件包作为分割算法软件，它可以将模型网格模型按指定的块数进行快速、均匀的分块(分块效果如图1所示)。

图1 网格模型Metis分块效果Fig.1 Mesh partitioned effects by Metis

2.2 块内顶点DCT变换和半脆弱水印嵌入

将原始模型进行主元分析校准预处理，并采用Metis软件分割成s块后，在每个分块内进行直角坐标空间到球面坐标空间的转换。即计算各顶点在以网格质心为原点的球面坐标系中的坐标值，包括半径r、经度角θ、纬度角φ。

每个分块内的顶点球面坐标的半径r值被分成一组序列，以第i个分块为例，可记为ri,1,ri,2,ri,3,.....ri,m，其中m为第i个分块内顶点的数目，将每个分块内的半径值序列进行一维DCT变换，每个分块可得到一组长度和块内顶点数目相同的DCT系数序列A，将每一组DCT系数序列取绝对值后，按从小到大的顺序排好序，为了使模型的失真最小，选择最小的三个DCT系数的绝对值作为水印载体，以第i个分块为例，从小到大的这三个系数依次记为αi,1,αi,2,αi,3。

采用密钥key生成一组长度为s(与模型的分块数目相同)，由1、0组成的伪随机二进制序列w作为嵌入用的半脆弱水印序列，每个模型分块用于隐藏一位水印，以第i个分块为例，水印的嵌入按式(1)方法进行。

(1)

各分组修改完毕后，按组内各元素原始位置和排序后位置之间的对应关系重新进行调整，得到修改后的DCT系数绝对值序列，然后参照原始序列A校对正负符号，得到嵌入水印后的DCT系数序列A′，与原始序列A相比，A′的各位元素正负符号一致，但由于嵌入水印的缘故，某些元素的幅值出现了少量变动。接下来将嵌入水印后的DCT系数序列A′进行DCT逆变换，得到组内模型各顶点嵌入水印后的半径r值，依据先前记录下的经、纬度角参数转换回直角坐标，得到该分块嵌入后的顶点直角坐标。每个分块依次执行上述步骤后，得到嵌入半脆弱水印后的三维模型Mw。

3 半脆弱水印提取算法与篡改定位方法描述

水印提取时无需原始网格参与，当怀疑模型被非法篡改时，将待测模型按前述的分块数目s进行Metis分块，重复前述嵌入水印的过程，每个分块内将待测模型的半径r值序列进行DCT变换，然后对DCT系数取绝对值后排序，最终可得到s组隐藏水印信号的三元组，在每一个三元组内提取半脆弱水印信号，以第i组为例，按式(2)的规则提取二进制水印序列。

(2)

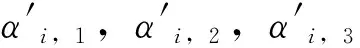
以原始密钥key生成原始水印w，与提取出的水印w'逐位进行匹配，当出现匹配错误时，意味着该位对应的网格分块被篡改，记录下该分块的编号，水印全部匹配完毕后，将有问题的网格分块以高亮的形式显示标记，用户即可确认篡改位置所在。

4 实验结果与比较

为了测试本文所提半脆弱水印算法的性能，在VC++和 OpenGL平台上对上述算法进行了编程实现，实验采用的标准测试模型为Bunny(35 947个顶点，69 451个三角形面片)、ManFace(16 374个顶点，32 744个三角形面片)和Happy Buddha(543 652个顶点，1 087 716个三角形面片)，嵌入的半脆弱水印为一组以密钥key生成，由1、0组成的二进制伪随机序列，水印序列的长度与模型分块的数目相同。在实验结果和分析部分，分别从水印透明性、水印容忍网格正常数据处理能力、水印对局部恶意攻击的定位能力等方面对算法性能进行了评价。另外，从容忍正常数据处理能力和对局部恶意攻击的定位能力方面，将本算法和其他网格模型半脆弱水印算法进行了比较。

4.1 水印透明性评价方法和模型分块数目的选择

4.1.1 水印透明性评价方法 本文采用的水印透明性评价方法包括几何误差评价和视觉失真评价两类：

1) 几何误差评价。

采用顶点三维直角坐标的信噪比(SNR)作为评价指标，记为SNRmesh，计算公式如式(3)。

SNRmesh=

(3)

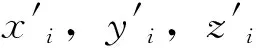
2) 视觉失真评价。

为了客观的评价模型视觉失真，本文采用模型截图采样的PSNR平均值来衡量[14]：选择8个观测视角，计算嵌入水印前后模型截图的PSNR(峰值信噪比)，然后取平均值，记为PSNRimage，将其作为模型视觉失真程度的客观评价指标，该值越大表示模型视觉失真越小。

4.1.2 网格模型分块数目的选择 在本算法中，增加分块数目虽然可以提高篡改定位的精度，但却会导致水印透明性下降，原因为水印嵌入时只固定改变分块内1个DCT系数的值，而各分块生成的DCT系数的数目与其块内顶点的数目相等，所以块内顶点数目越多，顶点几何数据受扰动的幅度就越小。从客观指标来看(参见表1)，随着模型分块数目的增加，SNRmesh值和PSNRimage值均呈递减趋势，说明水印的透明性随着分块数目增加而下降，当分块数目过多时，肉眼将会察觉出模型外观失真。为确保嵌入的水印具有良好的透明性，以PSNRimage≥35 dB作为阈值，将分块数目设定为Bunny模型600块、ManFace模型200块、Happy Buddha模型6 000块。

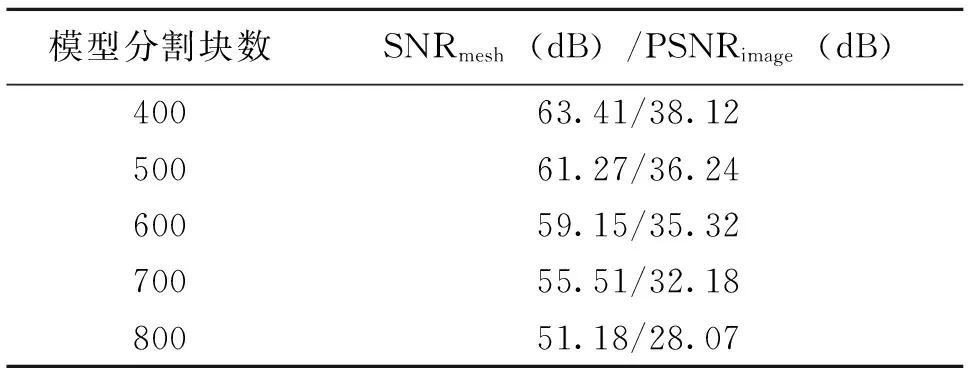
表1 不同分块数目时水印透明性评价结果(Bunny模型)Table 1 Evaluation results of watermark transparency by different partitioned numbers

4.2 水印敏感性评价方法和实验结果

当网格模型经历正常数据处理时，半脆弱水印应对此具备容忍能力，即不敏感，而当模型某部位遭受恶意攻击时，隐藏在该部位的半脆弱水印则应做出相应改变，以实现篡改检测定位。水印对模型改动的敏感程度可以提取出的半脆弱水印序列和原始半脆弱水印序列之间的相似性Sim作为评价指标，如式(4)。

(4)

其中w(i)和w'(i)分别表示原始水印序列和提取到水印序列的第i位值，L为水印序列的长度。当Sim=1.0时，说明提取到的水印序列与原始水印序列可完整匹配，表示网格模型没被改动或只是经历了容许范围内的网格正常数据处理；当Sim<1.0时，说明提取到的水印与原始水印之间出现了匹配出错位，表示网格模型被恶意攻击或经历了超出容许范围的网格正常数据处理。

4.2.1 算法对模型RST相似变换处理的容忍能力分析及实验结果

1)模型平移处理。本算法中水印嵌入实际修改的是模型顶点至模型质心的距离(即半径值)，该距离不会随着模型平移发生改变，因此平移对水印提取不会产生影响。

2)模型各向一致缩放处理。当模型进行各向一致缩放处理，表现为模型的所有顶点的几何数据同时缩放了相同倍数，即所有顶点在球面坐标空间中的半径值同时缩放了相同倍数，进行分块及块内DCT变换处理后，得到的DCT变换系数及其绝对值也将同时缩放相同的倍数，本文所提算法将水印信号隐藏到三个DCT变换系数绝对值的线性关系中，当这三个系数的绝对值缩放相同倍数时，该线性关系并不会发生任何改变，因此各向一致缩放处理不会对水印提取造成任何影响。

3)模型旋转处理。在嵌入和提取水印之前，都对模型进行了PCA主元分析，将模型调整为同一姿态，确保水印可同步提取，因此可容忍模型的旋转处理。

实验结果也表明(参见表2)，本算法嵌入的半脆弱水印对RST相似变换处理表现不敏感，水印相关值都达到了最大值1.0。

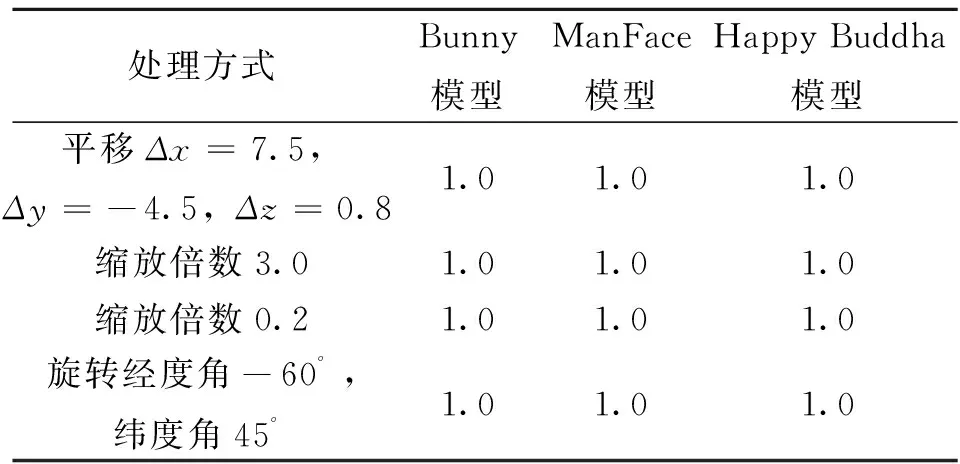
表2 模型RST相似变换处理后水印相关值Table 2 Watermark correlation values after model RST processing

4.2.2 算法对模型顶点随机噪声和顶点坐标值量化的实验结果

1)顶点随机噪声。

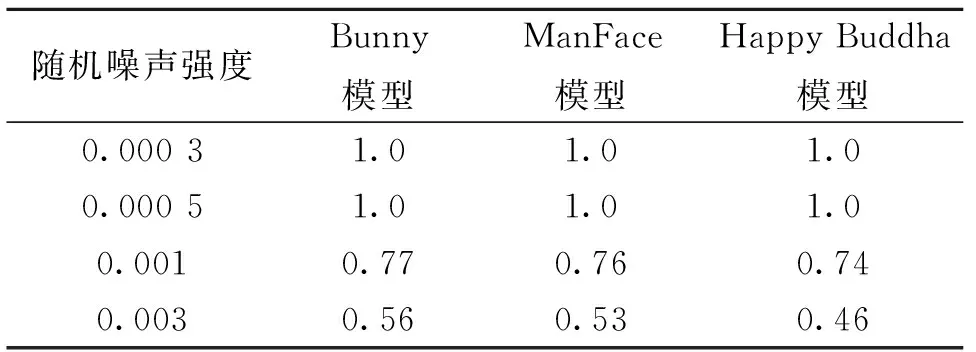
通过随机扰动嵌入水印后模型顶点的球面坐标半径值来添加随机噪声，表3给出的实验结果表明，算法嵌入的水印对低强度的噪声(如强度在0.000 5以下)具备一定抵抗能力(如图2(a)所示)，可满足算法对轻微噪声污染的容忍要求，但随着噪声攻击强度增大，水印相关性急剧下降，即高强度的噪声可理解为模型遭受了恶意攻击(如图2(b)所示)。

图2 顶点随机噪声造成的模型外观失真(Happy Buddha)Fig.2 Model appearance distortion by adding random noise on vertices

随机噪声强度Bunny模型ManFace模型HappyBuddha模型0.00031.01.01.00.00051.01.01.00.0010.770.760.740.0030.560.530.46

2)算法对模型顶点坐标值量化处理的实验结果。

目前绝大多数网格模型的顶点坐标均采用6位浮点数精度表示，表4的实验结果表明，当浮点数精度保持在4位或更高位数时，对模型外观造成的视觉失真较小，可认为其控制在“内容保持”的范围内，从实验结果可以看出，本算法嵌入的半脆弱水印对此敏感度较低，具备良好的容忍性；但当浮点数精度降低到2位数时，肉眼将很容易觉察到模型外观视觉质量出现失真(如图3所示)，此时模型的外观视觉失真已经超出了许可尺度，应视为恶意攻击，从实验结果可以看出，水印对此表现敏感，水印相关值急剧下降。

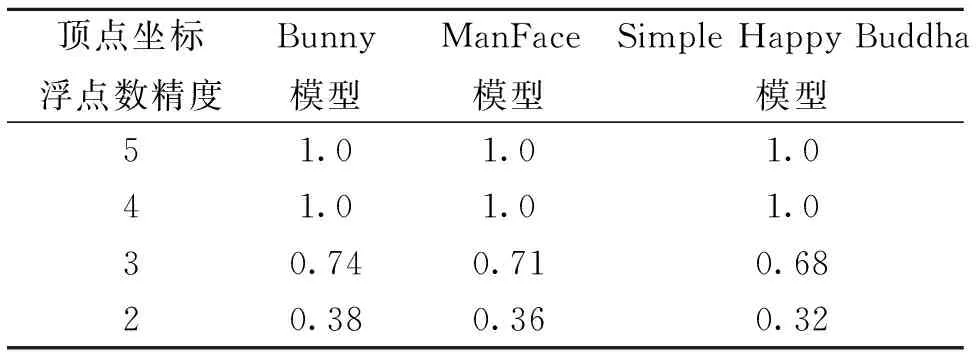
表4 顶点坐标量化处理后水印相关值Table 4 Watermark correlation values after quantization of vertex coordinates

图3 顶点坐标值量化对模型造成的外观失真Fig.3 Model appearance distortion by quantization of vertex coordinates

4.2.3 半脆弱水印对局部恶意攻击的定位能力测试 实验中采用了两种局部恶意攻击：局部变形和局部顶点随机噪声，半脆弱水印对此类攻击的检测定位结果参见图4。由于定位恶意攻击位置时以网格的分块为单位精度，一处攻击可能涉及多个分块，而实际攻击部位一般不会与Metis分块的轮廓吻合，因此实际得到的定位结果往往会略大于实际攻击的部位。实验结果表明，本文所提半脆弱水印算法对于恶意攻击表现敏感，当恶意攻击发生在局部位置时，可较准确的定位出篡改发生位置。

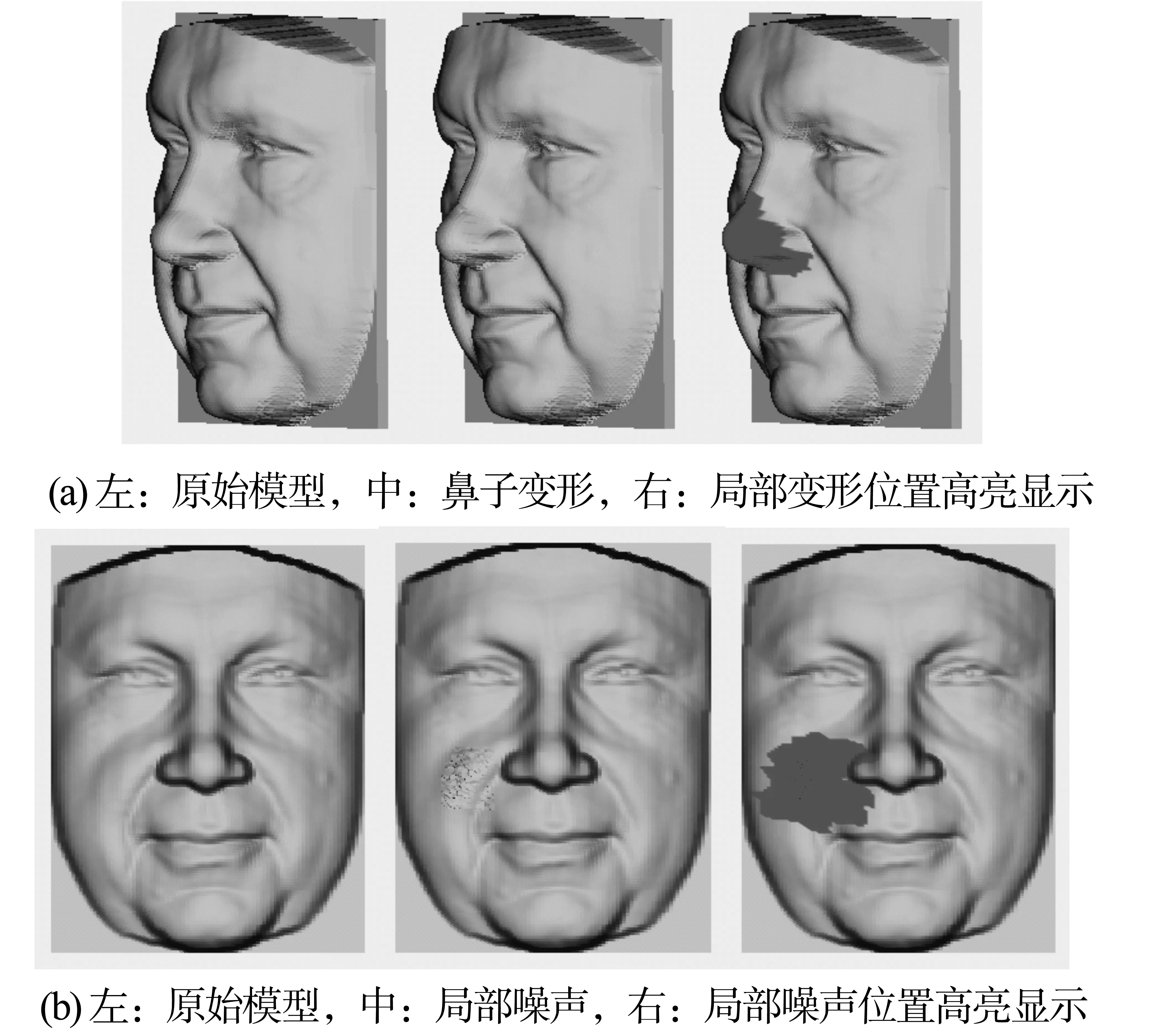
图4 半脆弱水印对局部恶意攻击的检测定位Fig.4 Detection and location of local malicious attacks

4.3 与其他三维网格模型半脆弱水印算法的比较

与本算法进行比较的网格模型半脆弱水印算法为Wu[9]的算法、Cho[10]的算法、Lin[11]的算法、Chou[12]的算法。与其他算法相比，本算法的主要优点为可容忍较多类型的网格模型正常数据处理，且能实现篡改位置的可视化定位标识。具体比较结果如表5所示。

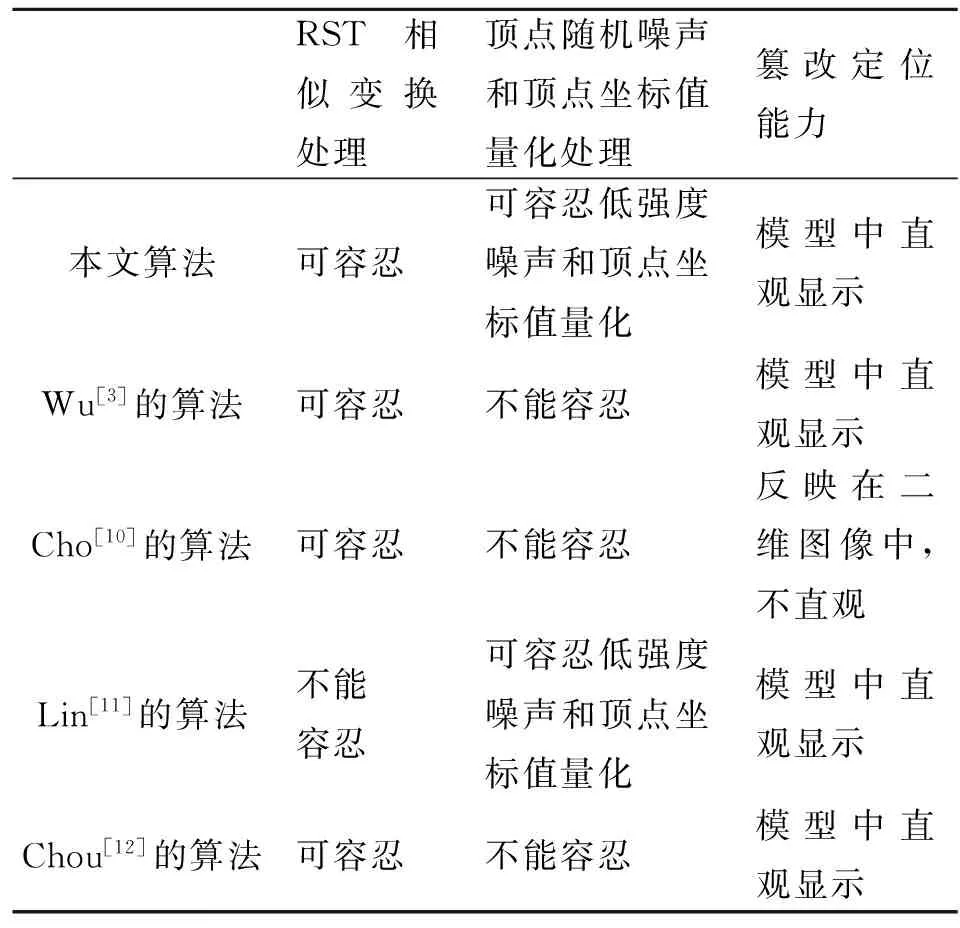
表5 与其他半脆弱水印算法的比较结果Table 5 Compared results with other semi-fragile watermarking algorithms

5 结 语

本文提出了一种基于内容级认证的网格模型半脆弱水印算法，网格分割处理后，在每个分块的顶点几何数据的DCT变换域系数中都嵌入1位半脆弱水印信号，确保水印对模型的完整覆盖，怀疑网格模型被非法篡改时，将提取出的水印序列与原始水印序列按位匹配可定位出篡改位置所在。在容忍网格正常数据处理方面，水印可不受RST相似变换处理影响，同时在模型“内容保持”的前提下，可容忍较低强度的顶点坐标值量化处理和随机噪声处理；而当网格模型遭受恶意攻击时，水印则表现敏感，可较准确的定位出篡改位置，并能以直观的可视化形式对其做出定位标记。

[1] 周燕, 张德丰, 马子龙. 基于压缩传感的图像哈希水印算法研究[J]. 中山大学学报: 自然科学版, 2010, 6(49): 58-63.

[2] 蔡龙飞，赵慧民，方艳梅. 一种公钥密码体制下指纹识别与数字水印的身份认证协议[J]. 中山大学学报: 自然科学版, 2013, 4(52): 51-57.

[3] 王国栋 刘粉林 汪 萍 耿楠楠. 一种篡改检测与篡改定位分离的图像认证方案[J]. 计算机学报, 2013, 10(30): 1880-1888.

[4] LUO M，BORS A G. Surface-preserving robust watermarking of 3-D shapes[J], IEEE Transactions on Image Processing, 2011,20(10):2813-2826.

[5] ZAFEIRIOUS S, TEFAS A, PITAS I. Blind robust watermarking schemes for copyright protection of 3D mesh objects[J]. IEEE Transactions on Visualization and Computer Graphics 2005, 11(5):596-607.

[6] CHO J W, PROST R, JUNG H Y. An oblivious watermarking for 3-D polygonal meshes using distribution of vertex norms[J]. IEEE Transactions on Signal Processing, 2007, 55(1):142-155.

[7] YEO B L, YEUNG M. Watermarking 3D objects for verification[J]. IEEE Computer Graphics and Applications, 1999, 19(1):36-45.

[8] CHOU C M, TSENG D C. A public fragile watermarking scheme for 3D model authentication[J]. Computer-Aided Design, 2006, 38(9):1154-1165.

[9] WU H T, CHEUNG Y M. A high-capacity data hiding method for polygonal meshes[C]. Springer：LNCS, Volume(4437), 2007:188-200.

[10] CHO W H, LEE M E, LIM H, et al, Watermarking technique for authentication of 3-D polygonal meshes[C]. Springer：LNCS, Volume(3304), 2005:259-270.

[11] LIN H Y, LIAO H. Authentication of 3-D polygonal meshes[C]. Springer：LNCS, Volume(2939), 2004:168-183.

[12] CHOU C M, TSENG D C. Affine-transformation-invariant public fragile watermarking for 3D model authentication[J]. IEEE Computer Graphics and Applications, 2009, 29(2):72-79.

[13] 崔晨旸.三维模型检索中关键技术的研究[D]. 杭州：浙江大学，2005.

[14] 孙树森.三维模型数字水印技术及防重构技术研究[D]. 杭州：浙江大学，2006.