一类带有Crowley-Martin反应函数的捕食-食饵模型的定性分析*
李海侠, 李艳玲
(1.陕西师范大学数学与信息科学学院, 陕西 西安 710062;2.宝鸡文理学院数学系, 陕西 宝鸡 721013)
近年来,许多专家研究了生物数学中模拟各种系统的反应扩散方程。由于物种动力系统中捕食者和食饵之间关系的普遍性和重要性,所以在生态数学中最重要的研究之一就是考察捕食者和食饵之间的关系。因此,带有各种不同反应函数和不同边界条件的捕食-食饵模型被许多生物学家和数学家所青睐。这些研究包括了经典的Holling 型,Beddington-DeAngelis型,比率依赖型和改进的Leslie-Gower 型的反应函数。可见文献[1-8]。
然而,目前对于带有Crowley-Martin(C-M)反应函数的捕食-食饵模型的研究并不多见,可看文献[9-10],作者讨论了带有C-M反应函数的食物链和捕食-食饵常微模型,得到了正常数平衡解的局部、全局稳定性和系统的持久性。C-M 反应函数
f(u,v)=bu/(1+cu+ev+ceuv)
是一类依赖捕食者的经典反应函数之一。这里正常数b,c和e分别描述了捕食者的捕获率、处理时间和捕食者间的强度。它与Beddington-DeAngelis反应函数很像,不同之处在于分母多了体现物种间相互干扰的一项ceuv。而且,无论某个捕食者目前是否寻找食饵,C-M反应函数都允许存在捕食者之间的干扰,这是比B-D 反应函数优越之处,也非常符合现实中的一些生物现象。因此研究带有C-M反应函数的模型具有很大的生物意义。显然,如果c=0,e=0,则C-M反应函数就会变成Holling-I 反应函数;如果c>0,e=0,则C-M反应函数就会变成Holling-II 反应函数。
本文在齐次Dirichlet 边界条件下讨论如下带有C-M反应函数的捕食-食饵模型
(x,t)∈Ω×(0,∞),
(x,t)∈Ω×(0,∞),
u(x,t)=v(x,t)=w(x,t)=0,
(x,t)∈∂Ω×(0,∞),
u(x,0)=u0(x)≥0,≢0,x∈Ω,
v(x,0)=v0(x)≥0,≢0,x∈Ω,
w(x,0)=w0(x)≥0,≢0,x∈Ω
(1)
其中Ω∈RN是带有光滑边界∂Ω的有界区域。系统(1)是三物种的捕食-食饵模型,其中u是食饵,v和w是两个以u为食物的捕食者,而且v和w相互竞争的捕食u。d是食饵u的增长率。k代表了u的容纳能力。r1和r2代表了转化率。p1和p2表示两捕食者之间的相互竞争率。q1和q2是两捕食者的死亡率。初值u0(x),v0(x)和w0(x)是连续函数。参数d,k,bi,ci,ei,pi,qi,ri(i=1,2)都是正常数。如果系统(1)没有捕食者w且e1=0,则(1)成为带有Holling-II反应项的两物种捕食-食饵模型。文献[4]和[11]在Neumann边界条件下讨论了该模型,运用Leray-Schauder度理论和分歧理论研究了非常数平衡态正解的存在性和不存在性。文献[12]考虑了带有非单调反应项的类似两物种捕食-食饵模型,利用谱分析和分歧理论研究了系统分歧解的存在性和稳定性。而且,我们也指出文献[1,13,14]在Neumann 边界条件下分别讨论了带有B-D反应项和非单调反应项的类似两物种捕食-食饵模型。
本文还将考虑系统(1)对应的平衡态系统
u=v=w=0,x∈∂Ω
(2)
正解的存在性和不存在性。
种群的持续生存性是对生态系统稳定性的一个重要刻画,是人们普遍关注的问题。而且,从生物意义上讲,研究物种的共存条件对捕食-食饵模型有很现实的生物意义。
1 预备知识
为得到重要的结论,首先给出一些预备知识。

-Δφ+q(x)φ=λφ,x∈Ω;φ=0,x∈∂Ω
则λ1(q)连续依赖q,λ1(q)是简单的。而且,如果q1≤q2,q1≢q2,则λ1(q1)<λ1(q2)。为了简单起见,定义λ1(0) 为λ1。
考虑如下问题
-Δu=uf(x,u),x∈Ω;u=0,x∈∂Ω
(3)

(H1)f(x,u)关于x是Cα-函数,其中 0<α<1;


定理1[16]假设f(x,u)满足(H1),(H2)和(H3)。则
(ii) 如果λ1(-f(x,0))≥0,则(3)没有正解只有零解。而且,平凡解u(x)=0全局渐近稳定;
(iii) 如果λ1(-f(x,0))<0,则(3)有惟一全局渐近稳定的正解。此时,平凡解u(x)=0不稳定。
考虑如下的非线性问题
(4)
由定理1可知,若ar>λ1,则(4)有惟一正解。定义惟一正解为Θar。特别地,Θa≤k且Θa连续依赖a。而且,如果a>λ1,e>λ1,a≤e,则Θa≤Θe。
2 正平衡态解的存在性和不存在性
本节通过考察系统(2)的二重分歧给出系统(2)正解存在的充分条件。我们同时将q1和q2作为分歧参数,利用空间分解和隐函数定理讨论系统(2)关于(Θd,0,0)的二重分歧,进而给出正解的近似表达式。
首先由上下解方法可得系统(2)的共存解的先验估计。
引理2 如果r1k>q1(1+c1k),r2k>q2(1+c2k), 则系统(2)的任意共存解(u,v,w)有先验估计
u(x)≤M1,v(x)≤M2,w(x)≤M3


V=0,x∈∂Ω
(5)

其次给出系统(2)共存解存在的充分条件和必要条件。
引理3 如果系统(2)有共存解,则
证明假设(u,v,w) 是系统(2)的共存解。 类似引理2可知d>λ1且u≤Θd。则由系统(2) 的第二个方程和引理1可得



x∈Ω;v=0,x∈∂Ω,
x∈Ω;w=0,x∈∂Ω
也有惟一正解。记惟一正解分别为v*和w*。记
引理4 假设(d,q1,q2)∈E。如果系统(2)有共存解(u,v,w),则
(6)
证明类似引理2由上下解方法可证得。
引理5 如果 (d,q1,q2)∈E。则系统(2)有解(u,v,w),且 (6) 式成立。
证明令

引理6 如果(q1,q2,u,v,w)是系统(2)的非负解且v≢0,w≢0,则-q1>λ1-r1/c1,-q2>λ1-r2/c2。
证明类似引理3可证得。
注本小节假设λ1c1 令L(q1,q2)是系统(2)在(Θd,0,0)处的线性化算子。则 L(q1,q2)= 这里 (7) 其中M=(m1,m2,m3)T∈E2,0<ε<δ,γ是参数。 G(M,ε1,ε2;ε)= (8) (9) 于是,综合上述,我们有下面的结论。 最后,给出系统(2)共存解不存在的充分条件。 定理3 如果下面的条件之一成立,则系统(2)没有共存解。 (i)d≤λ1; (iv)d>λ1且q1+r1k/(1+c1k)≤λ1; (v)d>λ1且q2+r2k/(1+c2k)≤λ1。 证明(i) 、(ii)和(iii)由引理3易得。下面证明(iv)、(v)类似可得。假设系统(2)有共存解(u,v,w),由引理2可知u(x)≤k。则由引理1和系统(2)的第二个方程可得 与已知条件矛盾。因此结论成立。 本节利用比较原理考察系统(1)的渐近行为。由抛物系统的上下解方法易知系统(1)有惟一正解。 首先给出系统(1)灭绝的充分条件。 定理4 设(u,v,w)是系统(1)的正解。 (i)如果d≤λ1,则当t→∞时,(u,v,w)→(0,0,0); 证明证明类似,因此只证(ii)。因为 u(x,t)≤Θd+σ (10) 因此,由系统(1)的第二个方程可得 vt-Δv≤ 再由定理1(iii)和比较原理可得 (11) 由σ→0的连续性再结合(10)式和(11)式可得当t→∞时,u(x,t)→Θd。 和方程 下面的定理给出系统(1)持续性的充分条件。 u(x,t)≤Θd+σ (12) 因此,由系统(1)的第二个方程可得 v(x,t)≤v*+σ,w(x,t)≤w*+σ (13) 另一方面,由系统(1)的第一个方程可知 x∈Ω;u=0,x∈∂Ω,t>0 (14) 因此, v(x,t)≥v*-σ,w(x,t)≥w*-σ (15) [v*-σ,v*+σ]×[w*-σ,w*+σ] 由σ的任意性并结合文献[18]中的推论2.1和定理2.1可知结论成立。 参考文献: [1]CHEN W Y,WANG M X.Qualitative analysis of predator-prey models with the Beddington-DeAngelis functional response and diffusion [J].Mathematical and Computer Modeling,2005,42:31-44. [2]郭改慧,李艳玲.带有保护区域的捕食-食饵模型平衡解的分歧与稳定性[J].陕西师范大学学报:自然科学版,2007,35:27-31. [3]WANG Z G,WU J H.Qualitative analysis for a ratio-dependent predator-prey model with stage structure and diffusion [J].Nonlinear Anal,2008,9:2270-2287. [4]PENG R,SHI J P.Non-existence of non-constant positive steady states of two Holling type-II predator-prey systems:strong interaction case [J].J Differential Equations,2009,247:866-886. [5]KO W,RYU K.Analysis of diffusive two-competing-prey and one-predator systems with Beddington-DeAngelis functional response [J].Nonlinear Anal,2009,71:4185-4202. [6]GUO G H,WU J H.Multiplicity and uniqueness of positive solutions for a predator-prey modelwith B-D functional response [J].Nonlinear Anal,2010,72:1632-1646. [7]ZHANG J F,LI W T,YAN X P.Hopf bifurcations in a predator-prey diffusion system with Beddington-DeAngelis response [J].Acta Appl Math,2011,115:91-104. [8]ZHOU J.Positive solutions of a diffusive predator-prey model with modified Leslie-Gower and Holling-type II schemes [J].J Math Anal Appl,2012,389:1380-1393. [9]UPADHYAY R K,NAJI R K.Dynamics of a three species food chain model with Crowley-Martin type functional response [J].Chaos,Solitons and Fractals,2009,42:1337-1346. [10]SHI X Y,ZHOU X Y,SONG X Y.Analysis of a stage-structured predator-prey model with Crowley-Martin function [J].J Appl Math Comput,2011,36:459-472. [11]KO W,RYU K.Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a prey refuge [J].J Differential Equations,2006,231:534-550. [12]JIA Y F,WU J H,NIE H.The coexistence states of a predator-prey model with nonmonotonic functional response and diffusion [J].Acta Appl Math,2009,108:413-428. [13]PANG Y H,WANG M X.Non-constant positive steady-states of a predator-prey system with nonmonotonic functional response and diffusion [J].Proc Lond Math Soc,2004,88:135-157. [14]CHEN X F,QI Y W,WANG M X.A strongly coupled predator-prey system with non-monotonic functional response [J].Nonlinear Anal,2007,67:1966-1979. [15]FIGUEIREDO D G,GOSSEZ J P.Strict monotonicity of eigenvalues and unique continuation [J].Commun Part Diff Eq,1992,17:339-346. [16]CANO-CASANOVA S.Existence and structure of the set of positive solutions of a general class of sublinear elliptic non-classical mixed boundary value problems [J].Nonlinear Anal,2002,49:361-430. [17]CRANDALL M G,RABINOWITZ P H.Bifurcation from simple eigenvalue [J].J Funct Anal,1971,8:321-340. [18]PAO C V.Quasisolutions and global attractor of reaction-diffusion systems [J].Nonlinear Anal,1996,26:1889-1903.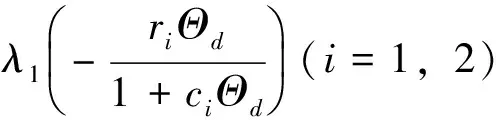

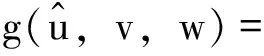




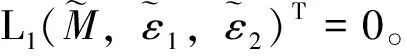
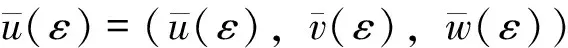

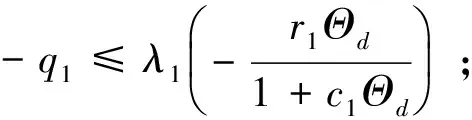

3 渐近行为









