基于随机森林的不平衡特征选择算法*

尹 华，胡玉平

(广东财经大学信息学院,广东 广州 510320)

分类是数据挖掘中最常见的一项任务，通过分类建立预测模型，可提供对未知问题的准确预测。尽管目前成熟的分类算法已被成功应用于各领域，但是信息技术发展带来的数据复杂度的提升，也对分类算法提出了新的挑战[1],其中具有大量属性的高维数据和类别分布不均匀的不平衡数据因在应用中的普遍性，成为目前研究的焦点。在诸如图像检索、入侵检测和生物信息挖掘等相关数据中都体现了高维和不平衡的双重特性。当分类高维数据时，由于特征空间大，产生的分类器复杂，数据容易过度拟合。特征选择可以减少数据维度，降低分类器的复杂度，使之更关注于提供丰富信息的特征向量。但传统特征选择方法大部分是以分布均衡的数据为研究对象，以优化总分类精度为基本目标，所以很少有方法在不平衡数据集得到理想的学习效果[2]。因此，针对不平衡数据设计有效的特征选择算法有其必要性。

尽管不平衡数据分类问题已经引起了研究界的重视，但是有关不平衡数据特征选择的研究仍然不够充分。文献[3]从统计的角度分析了含有丰富类别信息特征的分布特点，并提出了基于类别分布的特征选择框架。文献[4]从实验角度研究了不平衡问题上IG算法的困境，通过权重调整修改IG算法，使之能够较好应用于不平衡数据的特征选择。文献[5]综合考虑特征在正类和负类中的分布性质，结合四种衡量特征类别相关性的指标对文本中的特征词进行评分，使其能够更好解决传统特征选择方法在不平衡数据集上的不适应性。上述方法都是在文本分类的应用背景下研究不平衡特征选择问题，其解决思路是在已有常规特征选择方法的基础上，区别对待大类和小类的描述特征。刘天宇等在文献[6]中研究了故障诊断中的不平衡特征选择问题，在EasyEnsemble算法的基础上，结合基于预报风险误差的特征选择方法，提出了基于预报风险误差的EasyEnsemble算法PREE。PREE算法充分利用了集成算法的分类效果进行特征选择，但该方法得到的特征子集较大且冗余特征较多，且由于方法本身的计算特性，导致其不能有效地处理离散型特征。李霞等在文献[7]中采用先抽样，再特征选择，再集成投票的方法，提出了基于抽样集成的特征选择方法EFSBS。EFSBS可以获得较少的特征，但没有利用来自于分类算法的反馈。因此，应该设计新的能同时处理离散型和连续型特征，且可充分利用分类反馈的不平衡数据特征选择算法。

本文利用随机森林变量选择机制，针对不平衡问题，提出了一个不平衡随机森林变量选择方法(IBRFVS)。IBRFVS在平衡Bagging的基础上，构建多个决策树(基分类器)，针对每个基分类器，获取各特征重要性度量，通过对各基分类器所求得的特征重要性度量加权求和来获得最终的特征重要性序列。可在此序列上根据选择特征的数量由高至低进行特征选择。各基分类器所求得的特征重要性度量的权重由基分类器判定与投票评定的一致性决定。

1 随机森林

随机森林(Random Forest,RF)[8]是由Brieman于2001年提出的一个集成学习算法框架,分为两个步骤：1) Bagging获得多个子训练数据集；2) 在各训练数据集上建立决策树，决策树中每个结点的特征选择不是在全部特征空间，而是在随机选择的固定数量的特征空间中选择。随机森林通过在实例和特征上引入双重随机性来保证所产生基分类器的多样性；尽管在构造决策树时是在随机子空间中选择最佳分裂点，但由于最佳属性的计算并非随机的，而是根据一定的属性选择原则，一定程度上确保了基分类器的准确性。

在决策树构建过程中，树的每个结点都是以一定原则从众多特征中选择出的“重要”特征，这一过程实际上就是一个显示的特征选择过程。随机森林是对决策树的集成，也相应继承了决策树选择“重要”特征的能力，所不同的是，随机森林采用一种隐式的方式进行特征选择。随机森林变量选择(RVS)[9]是随机森林的一个副产品，是由Breiman提出的隐式的特征选择方法。当一个重要特征(对预测准确率有贡献)出现噪声时，预测的准确率应该明显减少。若此特征是不相关特征，则其出现噪声对预测准确率的影响应该不大。基于这一思想，在利用袋外数据(Out of Bag Data)预测随机森林性能时，若想获知某特征的重要程度，仅需随机修改该特征数值，而保持其他特征不变，由此获得的袋外数据预测准确率与原始袋外数据预测准确率之差体现了该特征的重要程度。

随机森林变量选择方法实际上是一种嵌入式的特征选择方法，充分利用了集成分类器构建过程所产生的分类模型。与PREE不同之处在于，PREE利用的是在特定特征上的结构风险变化，PREE在计算特定特征的AUC时，采用的是取特征平均值的方式；而随机森林变量选择方法基于的是无关特征对模型性能影响不大的思想，通过施加干扰来测试特征的准确程度。这种方法可以同时处理离散型数据和连续型数据，弥补了PREE的缺陷。同时在特征重要性度量计算时，充分利用了分类器的性能信息，相比于EFSBS仅考虑数据本身的特征相关性，在后续分类中，更易产生好的分类结果。

2 不平衡随机森林特征选择算法

高维数据处理的一种有效途径即通过特征选择降低特征维数，而不平衡数据处理的有效途径则是通过取样方法平衡数据。随机森林的两个步骤综合了此两项机制。由此可以考虑利用随机森林的算法机制设计合理的特征选择算法，用于同时处理高维不平衡数据。不平衡随机森林特征选择算法(IBRFVS)受随机森林算法启发，利用随机森林的构造过程，对不平衡数据集进行特征选择。由于随机取样将造成数据集的差别，单个取样数据集仅能代表数据的某个侧面，可能导致特征选择的不准确。如果能够获得取样数据的不同侧面，则可以从不同角度来进行特征选择，然后根据不同侧面的权威性来决定最终的特征选择结果。

2.1 算法描述

假设原始训练数据集为D，属性个数为M，欠取样后数据集为UnderSamplingD，个数为N，算法框架如图1所示。

图1 IBRFVS算法框架

IBRFVS的算法分为以下几个步骤：

1)用欠取样方法获得多个与小类实例数量相同的大类实例集；

2)在小类实例集上有放回取样获得与大类实例集相同数量的数据集；

3)将小类实例集与大类实例集组合获得多个平衡数据集UnderSamplingDi(i=1,…,N);

4)ForUnderSamplingDi(i=1,…,N)

a.计算各特征重要性度量FMij(j=1,…,M)；

b.计算FMi的权重TreeConfidencei；

5)加权计算获得数据集的最终特征重要性度量值。

随机森林的Bagging步骤是对全部数据集进行Boostrap取样。但是对于不平衡数据集而言，为使多数类与少数类平衡，是对少数类Boostrap取样，对于多数类则采用欠取样方法。这样处理的好处是，构造了多个欠取样数据集，可以反映不同的欠取样结果，在这些不同的欠取样数据集上所做的特征选择比在单一欠取样数据集上包含更多的信息。在特征选择时，当特征数量特别多时，搜索空间将非常大，在随机子空间上构造决策树，是一种缩小特征空间的有效方法，而决策树算法计算分裂属性的过程也就是一个属性选择的过程，可以直接利用此过程选择重要特征。在每个UnderSamplingD数据集上都可以构造一棵在随机子空间中产生的决策树，也即获得一个特征重要性度量。N个UnderSamplingD可以获得N个特征重要性度量。这些特征重要性度量体现了各特征在不同UnderSamplingD数据集上的重要程度。但是每个UnderSamplingD所获得特征重要性度量的可信度是不同的，在此体现为权重，也即可信度高的，所赋予的权重越高。因此IBRFVS算法的关键是特征重要性度量的计算和权重计算。

2.2 特征重要性度量

IBRFVS采用随机森林变量选择方法(Ⅵ)来计算特征重要性度量值。Ⅵ的特征重要性度量的计算是基于Out-of-Bag样本的。基于Out-of-Bag样本测试算法性能或计算算法参数是当前常用的一种方法[10]。这种方法的好处是可以减少参数计算的时间。但是在IBRFVS中，由于采用欠取样方法平衡数据集中的类别，如果按照Out-of-Bag样本的获取方法，则会导致出现Out-of-Bag中的大类数据过多的情况。因此，IBRFVS采用k层交叉验证的方法来获取特征重要性度量值。Ⅵ计算特征重要性度量值时，需要在每个特征上引入噪声之后进行交叉验证对比，以确定特征重要性程度。而随机森林需要构造多棵决策树，特征数量增加且k的层数增加时，算法运行时间将随之增加。因此在k的取值上采用最简单的交叉验证方法-holdout方法的思路，即每次用于验证的数据量不超过总数据量的三分之一。由此将k取值为3，将数据集随机分为3个不相交的子集，重复执行分类算法3次，取三次平均值作为最终的性能评价。单棵树的特征重要性度量值的计算方法如图2所示。

图 2 计算单棵树的特征重要性度量值

第j个属性的特征重要性度量值由Acc和AccFj的差值决定，其中Acc代表的是扰动属性值前的分类准确率，而AccFj代表的是扰动第j个属性的值后的分类准确率。由于采用三层交叉验证，每个UnderSamplingD分为三份，三份数据交叉作为测试数据集，因此，在同一UnderSamplingD数据集上，Acc和AccFj需要计算三次，最终的特征重要性度量值FMij是由三次所产生的平均差值决定。

其中i代表第i个UnderSamplingD数据集，第j个特征，k代表第k层数据。

2.3 权重度量

当大类数据与小类数据严重不平衡时，对大类数据欠取样可能产生差异性较大的UnderSamplingD数据子集。在此数据子集上所建立的树的准确率也将有所区别。假若把N个UnderSamplingD对于特征重要性的判断看做N个专家的判断，如EFSBS一样，可以考虑采用多数投票的方式。这种方式是基于各个专家的判断能力相同的假设上。实际上，由于UnderSamplingD的多样性，其准确性是不同的，由此，基于不同UnderSamplingD所做的特征重要性的判定能力也是不同的，应该赋予其不同的权重。BRFVS认为与最终集成判定一致度高的基决策树应该具有更高的权重，其所获得的特征重要性度量值具有更好的可信度。假设存在一个实例数为S的测试数据集，有N个UnderSamplingD数据集产生的N棵决策树。根据决策树的预测结果可获得一个S×(N+2)的矩阵，矩阵的行代表要预测的实例，矩阵的前N列分别代表N棵决策树，第N+1列代表集成投票的结果，在前N列中超过半数的判定，确定为第N列的最终结果，第N+2列代表测试数据集的实例类标号。则第i棵决策树的判定可信度可通过下式计算

AccEnsemble

其中TreeConfidencei表示第i棵树的可信度，Treeij表示第i棵树对第j个实例的预测结果，Ensemblej表示对第j个实例的集成预测结果。AccEnsemble表示的是集成预测准确率，即Ensemble与Original的一致性程度。由于每棵树的AccEnsemble都是相同的，TreeConfidencei与AccEnsemble相乘后所获得排序结果是一样的。之所以仍然需要加入这一影响因素，是为了缩小权重间的绝对差距，同时展现集成整体效果对于特征重要性度量的影响。表1为一个N=5,S=5的一致性度量矩阵。

表1 N=5,S=5的一致性度量矩阵

不考虑AccEnsemble因素，分别计算出Treei的可信度。

TreeConfidence1=1,TreeConfidence2=0.4,TreeConfidence3=0.8,TreeConfidence4=0.8,TreeConfidence5=0.4

考虑AccEnsemble因素，分别计算出Treei的可信度。

TreeConfidence1=0.8,TreeConfidence2=0.32,TreeConfidence3=0.64,TreeConfidence4=0.64,TreeConfidence5=0.32

特征权重计算时还需要考虑的一个问题就是测试数据集问题。由于特征权重计算的一个关键因素是集成性能。而集成性能是针对原始的整个数据集的。因此，可以借鉴Out-of-Bag的思想，构造欠取样后的Out-of-Bag数据集。欠取样后的Out-of-Bag数据集由两部分组成，一部分是小类Bootstrap后未取样的数据集，另一部分是大类欠取样后未取样的数据。

IBRFVS用于计算特征重要性度量值所使用的数据集是交叉验证数据集，而在计算特征权重时所使用的数据集是Out-of-Bag数据集。前者是平衡数据集，后者是不平衡数据集。区别对待的原因在于：特征重要性度量是在平衡数据集上获得，针对的是单棵决策树，此时用交叉验证的方法获得的是单棵决策树在某一种欠取样数据上对特征重要程度的一个判断。而基决策树的权重则是由该决策树对于集成所做的贡献决定的，随机森林分类的原始数据集是一个不平衡数据集，采用不平衡的Out-of-Bag数据测试当次集成的性能是合理的。通过每棵树确定所有特征的重要性度量值FM后，乘以各树的可信度TreeConfidence，求平均即可获得最终的特征重要性度量值FinalⅥ。

3 实验验证

IBRFVS算法的实验验证由两部分组成：算法参数选择和与预处理方法对比验证。实验数据集选自UCI数据集[11]。由于UCI数据集的数据不存在典型的不平衡特性，我们将多类问题转化为二分类问题，使数据集呈现了较为明显的不平衡特性。在二分类中，某一类比例低于50％的一定程度则展现了不平衡特性。在此，将不平衡程度分为四个级别：极高、高、中、低。其中正类比例在0～5％的范围属于极度不平衡，在5％～10％的范围属于高度不平衡，在10％～25％的范围则属于中度不平衡，在25％～40％的范围属于低度不平衡，当正类比例超过40％时，数据类别达到基本平衡状态。由此构造了7个实验数据集，如表2所示。

表 2 高维不平衡实验数据集

不平衡特征选择的目的是为了更好的特征选择再取样，最终获得好的分类性能。因此可以采用预处理后的分类性能来评价IBRFVS算法的好坏。如果采用IBRFVS算法特征选择后取样的分类性能优于普通特征选择后取样的分类性能，则可认为该算法对于不平衡数据特征选择是有效的。因此，实验按照随机森林的不同超参数取值获得各数据集的特征选择结果后再取样得到预处理后的数据。在分类器评价方面，则选择不平衡数据分类中常用的AUC面积作为评价标准。对该数据分类后的AUC性能间接代表了IBRFVS算法的性能。

3.1 RF参数影响

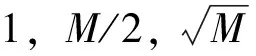
图3 各数据集在不同K值下的AUC值对比图

3.2 预处理对比分析

在对比实验中，我们将IBRFVS算法与未特征选择、过滤式特征选择和封装式特征选择对比，其中过滤式特征选择采用较为常用的信息增益(Information Gain,IG)特征选择，封装式特征选择则采用融合遗传搜索的Wrapper特征选择算法。

由于通过IBRFVS算法进行特征选择后，数据集仍然是不平衡的，因此在特征选择后，对数据集欠取样，获得平衡数据集，再用C4.5算法分类此平衡数据集，获得最终的分类性能AUC评价。IBRFVS算法输出的结果为数据集各特征重要性度量值。按照从大到小的顺序可获得最终的排列顺序。

图4 原始数据和处理后的AUC值

4 结 论

参考文献：

[1]YANG Q,WU X D.10 challenging problems in data mining research [J].International Journal of Inforamtion Technology & Decision Making,2006,5:597-604.

[2]蒋盛益，王连喜.不平衡数据的无监督特征选择方法[J].小型微型计算机系统，2013,34(1):63-67.

[3]靖红芳，王斌，杨雅辉，等.基于类别分布的特征选择框架[J].计算机研究与发展,2009,46(9):1586-1593.

[4]尤鸣宇,陈燕，李国正.不均衡问题中的特征选择新算法:Im-IG[J].山东大学学报：工学版,2010,40(5):123-128.

[5]张玉芳，王勇，熊忠阳，等.不平衡数据集上的文本分类特征选择新方法[J].计算机应用研究,2012,28(12):4532-4534.

[6]刘天羽,李国正，尤鸣宇.不均衡故障诊断数据上的特征选择[J].小型微型计算机系统,2009,30(5):924-927.

[7]李霞,王连喜，蒋盛益.面向不平衡问题的集成特征选择[J].山东大学学报：工学版,2011.41(3):.

[8]BREIMAN L.Random forests [J].Machine Learning,2001,45(1):5-32.

[9]GENUER R,POGGI J M,TULEAU-MALOT C.Variable selection using random forests [J].Pattern Recognition Letters,2010,31(14):2225-2236.

[10]李毓，张春霞.基于out-of-bag 样本的随机森林算法的超参数估计[J].系统工程学报,2011,26(4):566-572.

[11]ASUNCION A,NEWMAN D.UCI machine learning repository [G].[2014-04-30].http://archive.ics.uci.edu/ml/.

[12]GEURTS P,ERNST D,WEHENKEL L.Extremely randomized trees [J].Machine learning,2006,63:3-42.

[13]BERNARD S,ADAM S,HEUTTE L.Using random forests for handwritten digit recognition [C]//Ninth International Conference on Document Analysis and Recognition,2007,2:1043-1047.