基于速度概率和自适应速度值的差分进化算法

沈佳杰，江 红，王 肃

（华东师范大学信息科学技术学院，上海200241）

0 引 言

差分进化算法（differential evolution，DE）是由D.Storn和K.Price在1995年共同提出的一个在连续空间内启发式搜索的随机算法［1，2］。由于其优良的可扩展性和对于不同的优化问题的通用性，已经广泛应用到各个领域。

本文中通过引入速度概率和自适应速度值，提出了一种改进的二进制离散差分进化算法，通过理论推导改进的离散二进制差分进化算法较传统的离散差分进化算法在复杂的问题环境下，可以找到更好的问题最优解。通过对于经典的0－1背包问题的测试，改进的离散二进制差分进化算法较标准的离散差分进化算法较明显的改进，从而验证了本文中提出的速度概率和自适应速度值的差分进化算法的可行性。

1 标准差分进化算法与离散差分进化算法

1.1 标准差分进化算法

差分进化算法是基于群体智能的进化算法，其主要的操作有变异操作、交叉操作和选择操作，通过这3种不同操作，标准的差分进化算法［1，2］可以高效地找出函数的最优值，其主要定义如下:

个体种群由N个独立的个体组成，记为

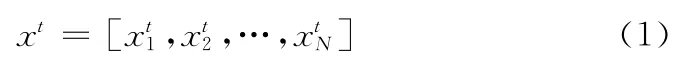
其中N为种群数。

每一个个体i是一个D维向量，记为

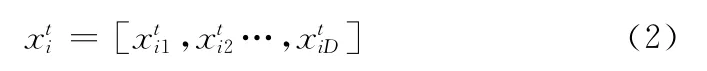
其中D为问题维数。

类似于遗传算法，需要通过差分进化算法中的变异、交叉和选择操作对种群进行变换，从而找出最优值点。

1.1.1 变异操作

变异操作的主要作用是对于不同个体进行差分变换，从而产生新的变异个体。变异公式如下所示

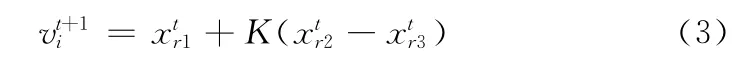
新的变异个体Vi由3个不同的个体通过式（3）计算而得。

1.1.2 交叉操作

交叉操作的主要作用是生成的实验个体与原个体进行交叉操作，从而生成新的变异个体。交叉操作如下所示

其中rand（0，1）为［0，1］之间随机数，CR为交叉概率其取值在［0，1］之间，rnbr（i）是指第i个个体的向量标号。

如式（4）所示，交叉操作的本质是将变异个体与原个体在各个维度向量上以一定的概率进行交叉，生成新的实验个体ui。

1.1.3 选择操作

选择操作的主要作用是在个体进入下一步迭代时，在现在个体和实验个体中选择一个适应度较高的个体生成下一代的种群。选择操作如下所示

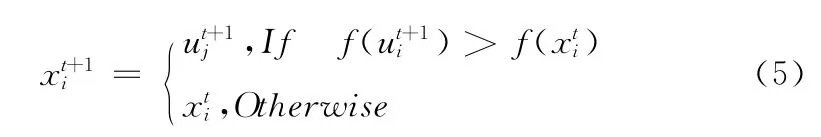
如式（5）所示，当改进实验个体的适应度大于原来个体适应度值，则采用改进后的实验个体，其他情况下采用原来个体。

1.2 标准差分算法步骤

标准差分算法步骤如下:

步骤1 初始化种群X1进入差分进化算法，确定CR，将迭代步数t设为1，同时设定最大迭代步数tmax。

步骤2 调用变异操作。通过式（3），计算所有个体的变异个体

步骤3 调用交叉操作。通过式（4），生成所有个体的实验个体

步骤4 调用选择操作。通过式（5），判断生成的实验个体是否比现存个体的适应度高，如果适应度高于现存个体，则让实验个体代替当前个体；否则，保留，生成下一代

步骤5 判断是否已经达到最优值或迭代步骤数是已经超过最大迭代步骤数，如果是，转向步骤6；否则转向步骤2。

步骤6 输出最优值点。

由于标准的差分进化算法主要是处理连续优化问题，不同的学者对标准的差分进化算法进行了改进以适应离散的优化问题的环境，如文献［3］通加入了贪心机制、文献［4］通过改进编码方式将差分进化算法应用到离散问题中，而对于进化算法本身的改进，如在差分进化算法中加入不同的机制［5，6］以及改进差分进化算法的算子［7，8］。于此同时，也有不少的文献也对于差分进化算法的研究现状进行了总结［9，10］，同时对于进化算法对于多目标问题的适用性也有许多文献进行了讨论，如文献［11］主要对于多目标收敛性进行了讨论，文献［12，13］主要对于主要对于多目标问题的描述和主要的进化解决算法进行了描述。下面我们主要介绍一种离散二进制的差分进化算法。

1.3 标准的离散二进制差分进化算法介绍

由于标准的差分进化算法，对于连续问题进行求解，所以已经有了许多的文献对于如何将差分进化算法应用离散问题进行讨论［3，4］。

这里我们主要介绍文献［3］中的离散差分进化算法。其与标准的差分进化算法的主要差别是将变异算子改进成如下公式

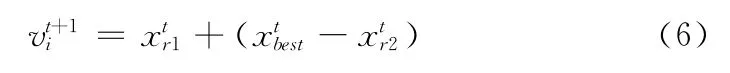
文献［3］中的二进制差分进化算法步骤数如下:

步骤1 初始种群X1进入差分进化算法，确定CR，将迭代步数t设为1，同时设定最大迭代步数tmax。

步骤6 判断是否已经达到最优值或迭代步骤数是已经超过最大迭代步骤数，如果是，转向步骤7；否则转向步骤2。

步骤7 输出最优值。

2 改进差分进化算法定义、步骤和性质

2.1 改进差分进化算法假设以及定义

本文中的算法的假设以及定义如下:

假设1:局部最优值的邻域内出现全局最优值的概率大于不是局部最优值点出现全局最优值的概率。

假设2:算法找到全局的最优值点可能需要不止一步迭代步骤。

假设3:在迭代步骤的过程中个体的适应度可能下降，且随着离散问题的扩大离散问题的局部最优解会增多。

定义1 对于每一个粒子点轨迹最优值点存在一个最优值向量，记为

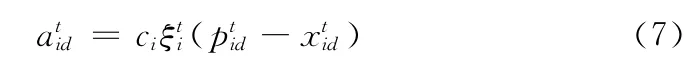
定义2 对于每一个粒子的每一维为存在一个速度值，这个速度值与迭代的步骤数成正比，称为自适应速度值，记为

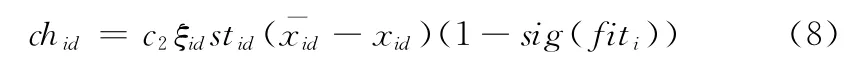
由以上的定义可知，如果当第i粒子的第k维为0时，以上函数为正，而当第i粒子的第k维为1时，以上函数为负，所以式（8）可以变形为

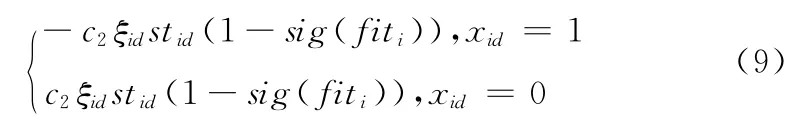
本文中的改进的变异算子是由定义1和定义2叠加组成，其变异个体的生成公式如下所示

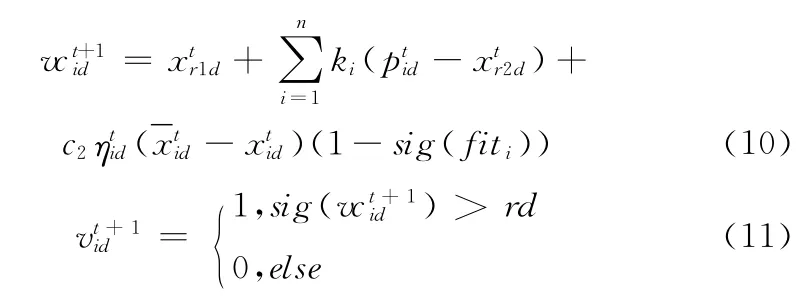
其中ki为缩放比例因子，为第t步时第r1个个体的位置、为第t步时第r2个个体的个体、为当前粒子的位置、为xid的取反、rd为一个［0，1］之间的随机数。

定义3 当实验个体优于原个体时，有一定的较小的概率选择原个体，而较大的概率选择实验个体，而当原个体优于实验个体时，有一定的较小的概率选择实验个体，而较大的概率选择原个体的选择算子，称为概率选择算子，记为

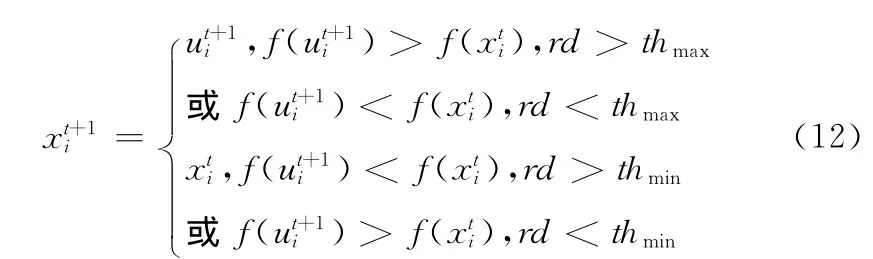
其中rd为一个（0，1）之间的随机数，thmax为［0，1］之间的一个数，thmin为［0，1］之间的一个数，thmax＋thmin＝1，thmax＞＞thmin。

2.2 改进差分进化算法步骤

本文中算法步骤如下:

步骤1 初始种群X1进入差分进化算法，确定CR，将迭代步数t设为1，同时设定最大迭代步数tmax。

步骤3 根据式（10）以及式（11），调用变异算子，计算速度概率以及变异个体。

步骤5 根据式（12），调用概率选择操作，比较生成的实验个体与原来个体，选择较优者生成下一代的个体。

步骤6 判断是否已经达到最优值或迭代步骤数是已经超过最大迭代步骤数，如果是，转向步骤7；否则转向步骤2。

步骤7 输出最优值。

2.3 改进差分进化算法的性质以及定理证明

本文中算法的性质以及定理证明:

定理1 如果所有的都在一步之内实验个体都不优于原个体的情况下，标准的离散差分进化算法将很难找到最优值点。

证明:

由于在标准的离散差分进化算法中，最后的选择算子，会比较实验个体与原个体并选择适应度较高的个体，如果所有的实验个体的适应值都小于原来的，则用于进化的实验个体将不会替换原来的个体，即陷入局部最优值，所以标准的离散差分进化算法将很难找到最优值点。

定理1说明标准的离散差分进化算法，如果个体种群生成的实验个体如果都小于，则算法会陷入局部最优解，这在一定的程度限制了标准的离散差分进化算法在高维环境下，找到全局最优解的能力。

推论1:如果问题规模过大的情况下，标准的离散差分进化算法已陷入早熟将很难找到全局最优值。

证明:

因为随着问题规模的变大，离散问题的局部解将增多，所以当所有的个体都陷入局部最优解的情况下，生成实验个体极可能小于原个体，而在这种情况下，算法将维持原始个体，即没有个体更新，因此标准的离散差分进化算法已陷入早熟将很难找到全局最优值。

定理2 本文改进的离散二进制差分进化算法，在所有的实验个体都不优于原个体的情况下，依然可以继续搜索全局最优值。

证明:

由于改进的离散二进制差分进化算法中的概率选择算子，有一定的概率选择适应度较差的个体，所以即使实验个体的适应度小于原个体的适应度，本文改进的概率选择算子依然又会有一定的概率选择适应度较差的实验个体以保证算法对于最优值搜索的进行。

由定理2可知，即使是在实验个体都不优于原先个体的情况下，依然可以继续进行全局最优值搜索，所以本文中离散二进制差分进化算法可以持续的进行最优值搜索。

推论2:改进的离散二进制差分进化算法，当个体数量和迭代步骤数足够的情况下，改进的离散二进制差分进化算法可以找到较好的全局最优值。

证明:

由于本文中的的离散二进制差分进化算法由于引入了概率选择算子，所以在个体陷入局部最优值的情况下，依然可以在一定的概率下，选择适应度较差的实验个体，所以算法容易跳出局部最优值，因此本文中的改进的离散二进制差分进化算法，当个体数量和迭代步骤数足够的情况下，可以找到较好的全局最优值。

3 实 验

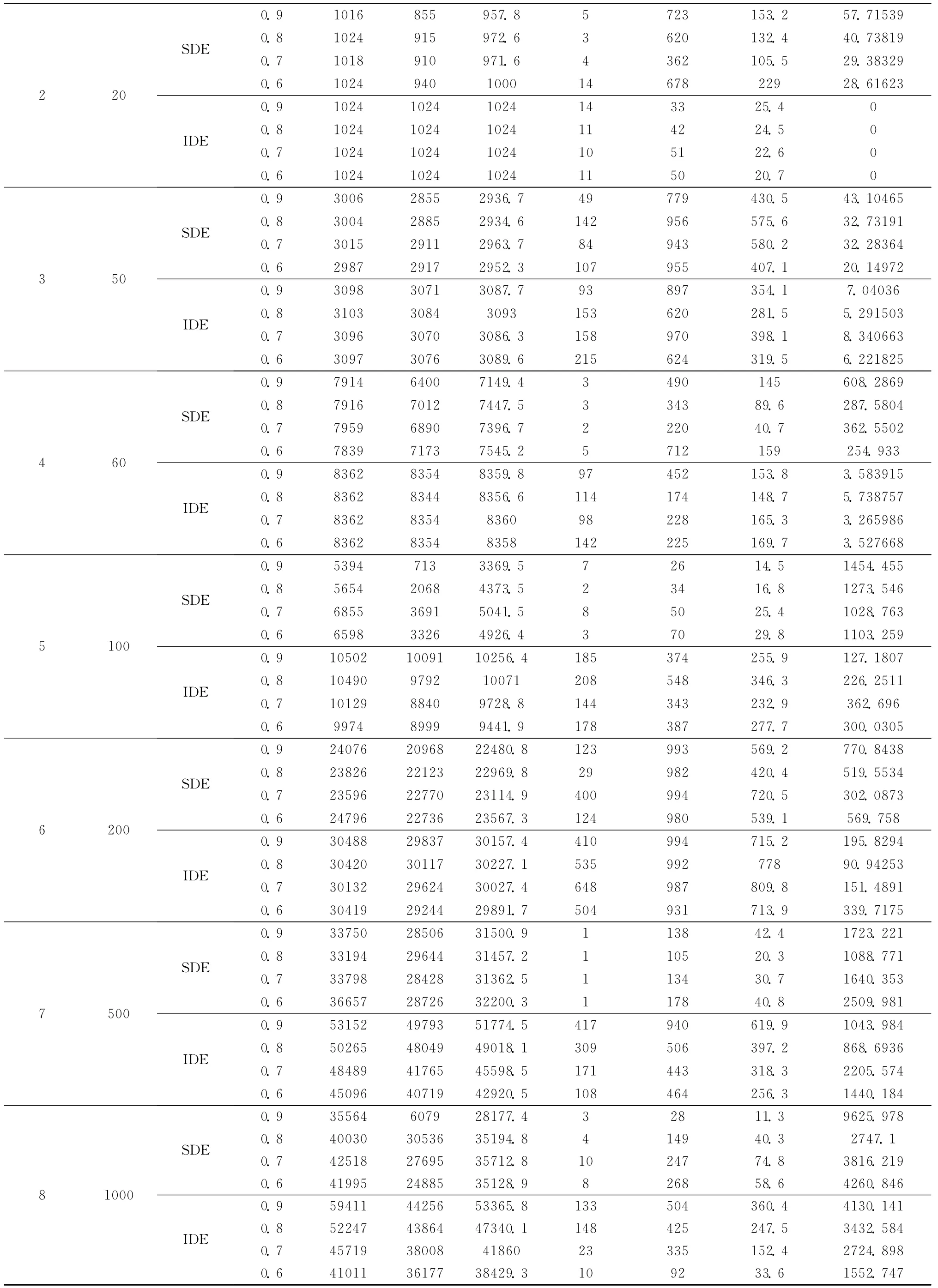
本文中使用经典的0－1背包问题进行测试［5］，本文对于物品数为10、20、50、60、100、500、1000八种不同的测试问题，在交叉概率为0.9、0.8、0.7、0.6这4种不同的条件下，分别进行10次独立的实验，表1中展示了本文中的4个测试用例，其中5－8问题用例中的数据随机生成。表2中主要展示了在不同问题用例下，标准的离散二进制优化算法和本文中改进的离散二进制算法的10次算法迭代中的所找到最优解，平均解和最差解以及各个不同的最优解之间的方差以及找到最优解时，二进制离散差分算法经过的最小、最大和平均的迭代步骤数。

其中SDE表示标准的离散粒子群算法，IDE表示本文中改进的离散二进制粒子群算法。

由表2可知，改进的离散二进制差分进化算法较标准的离散差分进化算法，在问题规模比较小的情况下（如问题实例1），标准的离散差分进化算法和本文中离散二进制差分进化算法都可以找到较好的最优值，而当问题规模较大时（如问题实例5－8），改进的离散二进制差分进化算法较标准的离散差分进化算法在最优值和标准方差稳定性方面具有一定的优势，在部分问题实例中（如问题5）最优值的差距接近于一倍。

图1（a）主要展示了在算法迭代终止时，不同的问题规模与算法找到的平均最优值之间的关系，图1（b）中主要展示了在算法迭代终止时，不同的交叉概率的条件下，不同的交叉概率与算法找到的平均最优值之间的关系。

表1 本文中实验中测试用例

表2 标准的离散二进制差分进化算法和本文中改进的离散二进制差分进化算法性能对比

SDE 2 20 0.9 1016 855 957.8 5 723 153.2 57.71539 0.8 1024 915 972.6 3 620 132.4 40.73819 0.7 1018 910 971.6 4 362 105.5 29.38329 0.6 1024 940 1000 14 678 229 28.61623 IDE 0.9 1024 1024 1024 14 33 25.4 0 0.8 1024 1024 1024 11 42 24.5 0 0.7 1024 1024 1024 10 51 22.6 0 0.6 1024 1024 1024 11 50 20.7 0 SDE 3 50 0.9 3006 2855 2936.7 49 779 430.5 43.10465 0.8 3004 2885 2934.6 142 956 575.6 32.73191 0.7 3015 2911 2963.7 84 943 580.2 32.28364 0.6 2987 2917 2952.3 107 955 407.1 20.14972 IDE 0.9 3098 3071 3087.7 93 897 354.1 7.04036 0.8 3103 3084 3093 153 620 281.5 5.291503 0.7 3096 3070 3086.3 158 970 398.1 8.340663 0.6 3097 3076 3089.6 215 624 319.5 6.221825 SDE 4 60 0.9 7914 6400 7149.4 3 490 145 608.2869 0.8 7916 7012 7447.5 3 343 89.6 287.5804 0.7 7959 6890 7396.7 2 220 40.7 362.5502 0.6 7839 7173 7545.2 5 712 159 254.933 IDE 0.9 8362 8354 8359.8 97 452 153.8 3.583915 0.8 8362 8344 8356.6 114 174 148.7 5.738757 0.7 8362 8354 8360 98 228 165.3 3.265986 0.6 8362 8354 8358 142 225 169.7 3.527668 SDE 5 100 0.9 5394 713 3369.5 7 26 14.5 1454.455 0.8 5654 2068 4373.5 2 34 16.8 1273.546 0.7 6855 3691 5041.5 8 50 25.4 1028.763 0.6 6598 3326 4926.4 3 70 29.8 1103.259 IDE 0.9 10502 10091 10256.4 185 374 255.9 127.1807 0.8 10490 9792 10071 208 548 346.3 226.2511 0.7 10129 8840 9728.8 144 343 232.9 362.696 0.6 9974 8999 9441.9 178 387 277.7 300.0305 SDE 6 200 0.9 24076 20968 22480.8 123 993 569.2 770.8438 0.8 23826 22123 22969.8 29 982 420.4 519.5534 0.7 23596 22770 23114.9 400 994 720.5 302.0873 0.6 24796 22736 23567.3 124 980 539.1 569.758 IDE 0.9 30488 29837 30157.4 410 994 715.2 195.8294 0.8 30420 30117 30227.1 535 992 778 90.94253 0.7 30132 29624 30027.4 648 987 809.8 151.4891 0.6 30419 29244 29891.7 504 931 713.9 339.7175 SDE 7 500 0.9 33750 28506 31500.9 1 138 42.4 1723.221 0.8 33194 29644 31457.2 1 105 20.3 1088.771 0.7 33798 28428 31362.5 1 134 30.7 1640.353 0.6 36657 28726 32200.3 1 178 40.8 2509.981 IDE 0.9 53152 49793 51774.5 417 940 619.9 1043.984 0.8 50265 48049 49018.1 309 506 397.2 868.6936 0.7 48489 41765 45598.5 171 443 318.3 2205.574 0.6 45096 40719 42920.5 108 464 256.3 1440.184 SDE 8 1000 0.9 35564 6079 28177.4 3 28 11.3 9625.978 0.8 40030 30536 35194.8 4 149 40.3 2747.1 0.7 42518 27695 35712.8 10 247 74.8 3816.219 0.6 41995 24885 35128.9 8 268 58.6 4260.846 IDE 0.9 59411 44256 53365.8 133 504 360.4 4130.141 0.8 52247 43864 47340.1 148 425 247.5 3432.584 0.7 45719 38008 41860 23 335 152.4 2724.898 0.6 41011 36177 38429.3 10 92 33.6 1552.747

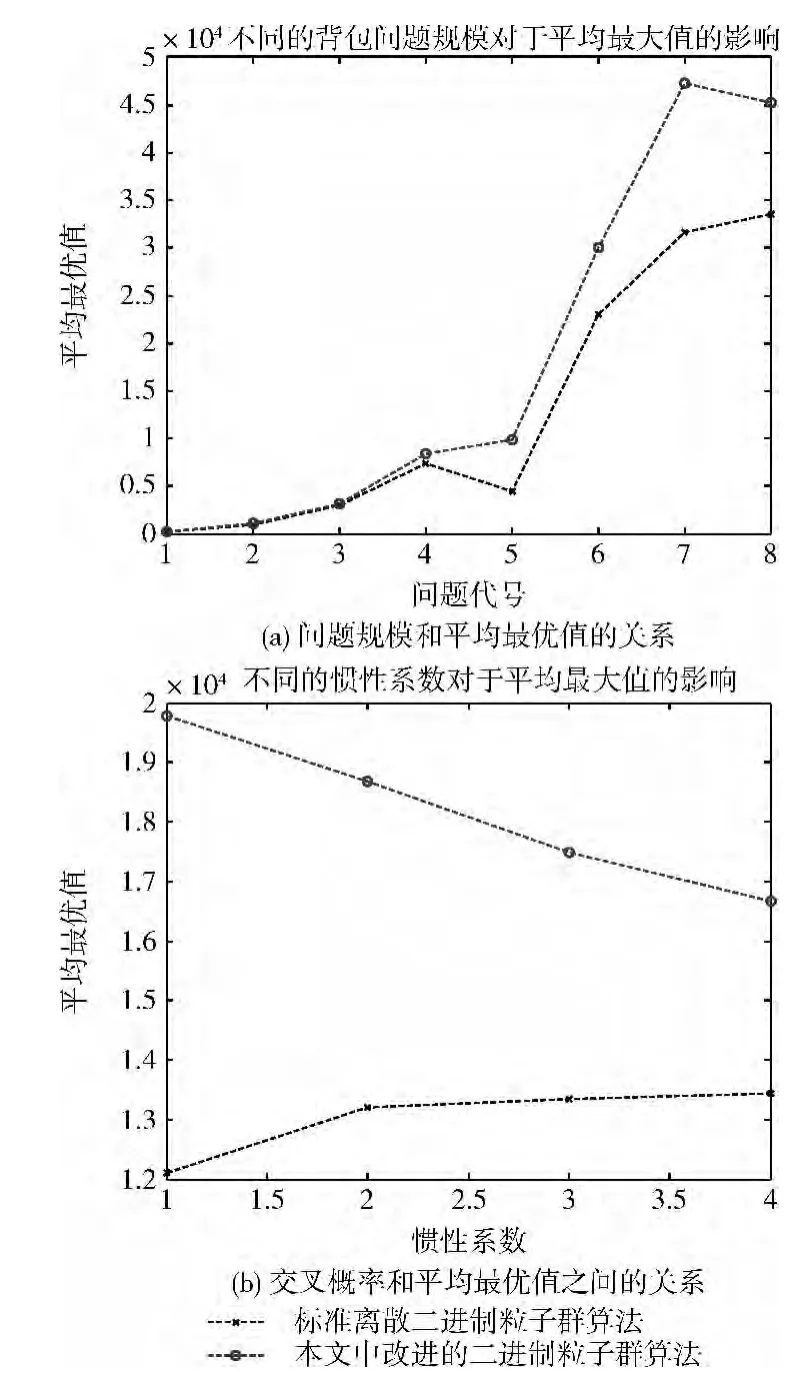
图1 迭代终止时，差分进化算法平均最优值的对比

如图1（a）可知，在问题规模较小时，标准的离散差分进化算法和改进的离散二进制差分进化算法都可以在算法迭代终止时找到比较好的最优值，而当问题规模比较大的情况下（问题实例5－8），改进的差分进化算法较标准的差分进化算法有较大的优势，在问题实例7、8中本文中的差分进化算法找到的最优值与标准的差分进化算法的最优值差距达到了近一倍。如图1（b）所示在不同交叉概率的条件下，改进的离散二进制差分进化算法比标准的离散差分进化算法更好的平均最优值。

图2主要展示了在部分问题实例中，标准的离散二进制差分进化算法和改进离散二进制差分进化算法迭代步骤数与算法所能找到平均最优值之间的关系:

如图2所示，在问题规模较小的情况下，改进的离散二进制差分进化算法与标准的离散差分进化算法都可以找到几乎相同的平均最优值，如图2（a）中标准的离散差分进化算法和本改进的离散二进制差分进化算法都可以在算法迭代的过程中找到较好的平均最优值，随着问题规模的扩大（如图2（b）－（d）），改进的离散二进制差分进化算法和标准的离散差分进化算法相同的迭代步骤数中，可以找到更好的最优值而平均最优值之间的差距逐步扩大，如图2（c）（d）中，当本文中的改进的离散二进制差分进化算法与标准的离散差分进化算法算法收敛时，两者之间的差距达到了将近一倍。

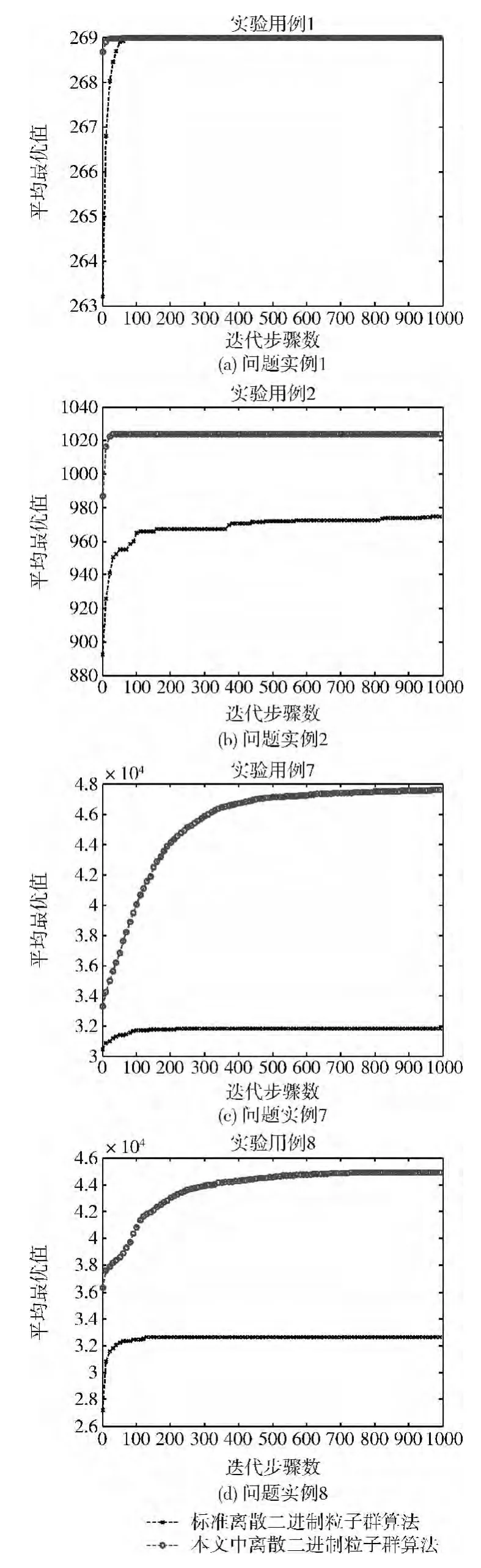
图2 算法迭代步骤数与平均最优值之间的关系

4 结束语

本文中通过速度概率和自适应速度值，提出了一个改进的差分进化算法，通过理论推导和实验证明改进的离散二进制差分进化算法较传统离散差分进化算法在问题规模较大时，可以在相同的优化条件下取得更好的最优化结果。

本文中虽然提出了一个改进的离散二进制差分进化算法并进行了理论证明以及实验验证，但是由于实验有限是否可以找到一种不同的实验问题条件下，通用的离散二进制差分进化算法，依然是一个值得研究的问题。

［1］Storn R，PRICE K.Differential evolution－a simple and efficient heuristic for global optimization over continuous spaces［J］.Journal of Global Optimization，1997（11）:341－359.

［2］Storn R，Price K.Minimizing the real functions of the ICEC＇96 contest by differential evolution［C］//Evolutionary Computation，1996.

［3］MIAO Shiqing，GAO Yuelin.Discrete differential evolution algorithm for solving 0/1 knapsack problem［J］.Journal of Chinese Computer Systems，2009，30（9）:1828－1830（in Chinese）.［苗世清，高岳林.求解0/1背包问题的离散差分进化算法［J］.小型微型计算机系统，2009，30（9）:1828－1830.］

［4］HE Yichao，WANG Xizhao，KOU Yingzhan.A binary differential evolution algorithm with hybrid encoding［J］.Journal of Computer Research and Development，2007，44（9）:1476－1484（in Chinese）.［贺毅朝，王熙照，寇应展.一种具有混合编码的二进制差分演化算法［J］.计算机研究与发展，2007，44（9）:1476－1484.］

［5］WU Lianghong，WANG Yaonan，YUAN Xiaofang，et al.Differential evolution algorithm with adaptive second mutation［J］.Control and Decision，2006，21（8）:898－902（in Chinese）.［吴亮红，王耀南，袁小芳，等.自适应二次变异差分进化算法［J］.控制与决策，2006，21（8）:898－902.］

［6］SHAO Liang.Differential evolution algorithm based on indivi－dual ordering and sampling［J］.Computer Engineering and Application，2012，48（1）:49－52（in Chinese）.［邵梁.基于排序采样策略的差分演化算法［J］.计算机工程与应用，2012，48（1）:49－52.］

［7］Epitropakis M G，Pavlidis N G，Plagianakos V P，et al.Enhancing differential evolution utilizing proximity－based mutation operators［J］.Evolutionary Computation，2011，15（1）:99－119.

［8］Zaharie D.Influence of crossover on the behavior of differential evolution algorithms［J］.Applied Soft Computing，2009，9（3）:1126－1138.

［9］YANG Qiwen，CAI Liang，XUE Yuncan.A survey of differential evolution algorithms［J］.Pattern Recognition and Artificial Intelligence，2008，21（4）:506－513（in Chinese）.［杨启文，蔡亮，薛云灿.差分进化算法综述［J］.模式识别与人工智能，2008，21（4）:506－513.］

［10］LIU Bo，WANG Ling，JIN Yihui.Advances in differential evolution［J］.Control and Decision，2007，22（7）:721－729（in Chinese）.［刘波，王凌，金以慧.差分进化算法研究进展［J］.控制与决策，2007，22（7）:721－729.］

［11］ZHOU Yuren，MIN Huaqin，XU Xiaoyuan，et al.A multi－objective evolutionary algorithm and its convergence［J］.Chinese Journal of Computer，2004，27（10）:1415－1421（in Chinese）.［周育人，闵华清，许孝元，等.多目标演化算法的收敛性研究［J］.计算机学报，2004，27（10）:1415－1421.］［12］XIE Tao，CHEN Huowang，KANG Lishan.Evolutionary algorithms of multi－objective optimization problems［J］.Chinese Journal of Computer，2003，26（8）:997－100（in Chinese）.［谢涛，陈火旺，康立山.多目标优化的演化算法［J］.计算机学报，2003，26（8）:997－100.］

［13］GONG Maoguo，JIAO Licheng，YANG Dongdong，et al.Research on evolutionary multi－objective optimization algorithms［J］.Journal of Software，2009，20（2）:271－289（in Chinese）.［公茂果，焦李成，杨咚咚，等.进化多目标优化算法研究［J］.软件学报，2009，20（2）:272－289.］