密度泛函理论对AlnTi2 (n=2～11)团簇结构和稳定性的研究

肖 培, 刘以良, 姜 明

(西南民族大学 电气信息工程学院, 四川 成都 610041)

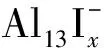
1 模型构建和计算方法

初始模型由3种方法得到,一是构建其可能存在的独立结构,二是采用生长法在Aln-1Ti团簇结构的基础上任意添加1个Ti原子,三是采用替代法,即在Aln+1Ti稳定结构的基础上任意替代1个Ti原子或从Aln+2稳定结构的基础上替代2个Ti原子从而得到候选的AlnTi2模型.因此,随着AlnTi2团簇尺寸的增加,候选结构的数量快速增长,模型优化耗时巨大.

基于密度泛函理论的第一性原理方法,使用软件包DMOL3程序对模型进行自洽场计算[25-27],为了确保精度,对Al原子采用全电子(AE)计算,同时采用双数值极化DNP基组.关于电子的交换关联势采用广义梯度近似(GGA),具体的泛函为BP,BP泛函是Becker的交换泛函与Perdew和Wang的修正泛函(PW91)的结合[28-29].自洽场的收敛精度为10-6a.u.,最大力、原子最大位移以及总能量的收敛精度分别为4.0×10-2Hartree/nm,5.0×10-2nm和10-5a.u.,而电子密度几何优化采用了Broyden-Fletcher-Goldfarb-Shanno(BFGS)方法[30].并且在优化过程中,所有的原子都没有限制其自由度.

为了确保所得到的优化模型对应着局域最小,对每一个稳定构型又进行了频率分析.当优化后的模型有多个虚频时,舍弃它;而当优化后的模型有1个或2个虚频时,将对这个模型做一些调整,然后重新优化,直到没有虚频为止.

2 结果与讨论

2.1几何结构对于AlnTi2每一个尺寸的团簇,因为大量的初始模型,所以也得到很多稳定的结构.图1只展示了能量最低的平衡几何结构以及2个能量次之的同素异构体.其中粉色小球代表Al原子,灰色小球代表Ti原子,且图1中的结构按能量从低到高的顺序依次标为na、nb、nc(n为Al原子的数量).另外,团簇几何结构的点群对称性,与基态的能量差也在图1中.

从图1中可以看到,Al2Ti2最低能量的结构是Ti2分子和Al2分子互相垂直,且拥有C2v对称性的四面体,它是在Al3Ti团簇基态结构基础上替换1个Al原子得来的.2b是拥有较高能量的平面棱形结构,2个Al原子和Ti原子分别处在相对的位置,它的结构接近于纯Al4团簇结构,而一维链状的Al2Ti2结构不能稳定存在,故只有2个平衡结构.从n=3开始就不存在二维平面结构.对于Al3Ti2,3a,3b和3c拥有相同的几何结构,只是Ti原子所占位置不同导致原子间的相互作用不同从而引起一定的形变.3a的对称性为C2v,而变形之后的3b的对称性降为Cs,他们的能量差为167 meV.3c结构的点群对称性为D3d,它们都是在Al4Ti团簇的4c结构基础上替代而成的.

Al4Ti2的基态结构是拥有D4d对称性的四角双锥结构,2个Ti原子之间的键长为0.267 7 nm,而与之垂直的相邻Al原子之间的距离约为0.318 nm,是在Al5Ti的5b结构上替代而成.另2个异构体分别是拥有对称性为C1和C2v的三角双锥带帽结构,其与基态的能量差分别为379和470 meV,是在Al3Ti2结构基础上添加1个Al原子生长而来.Al5Ti2的5a和5b结构是对称性为C2v的五环双锥体,2个Ti原子在2个五环中分别占据不同的位置,其能量差仅为38 meV.5c是1个带帽的双锥体结构,其点群对称性为Cs.他们分别是在Al6Ti团簇6a和6b结构基础上替代而得到的.

Al6Ti2的基态构型是一个点群对称性为C2的未封闭的五环双锥体,其中1个Ti原子在锥顶.6b的结构与6a相同,2个Ti原子都占据在环上位置,其与基态的能量差为167 meV.6c是1个封闭的五角双锥带帽结构,他与基态的能量差也仅为164 meV,其点群对称性为Cs.在Al7Ti2的稳定构型中,7a是在5c的基础上添加2个Al原子形成的,其对称性为Cs,而7b和7c构型为五角双锥的双带帽结构,其对称性为C1,值得一提的是7a和7b的能量差非常小,仅为2 meV,且7c的能量也只比7b的能量高73 meV.

Al8Ti2的稳定构型也分为2类,一类是双侧双带帽的六角双锥体8a和8c,其点群对称性为C2.一类是同侧三带帽的五角双锥体8b,其点群对称性为Cs,它是在Al9Ti团簇的基态结构上替换而成.这3个稳定构型的能量差也很小,8b和8c的能量比基态能量分别高88和160 meV.9a的结构看着与8a相似,但是是由2个相对的六角锥体组成,其中2个锥体的3个原子是重叠的,其对称性为C2.9b可以看成是在7b结构基础上添加2个原子所得,也可看成是正二十面体结构Al13去掉2个与Ti原子相对位置的Al原子所得,其对称性为C2v.9c构型可以看成是1个层状结构,一层为六角锥体,一层为棱形,其点群对称性为Cs,它是在Al10Ti团簇的10b结构基础上替代而成.9b和9c的能量分别比基态结构高177和197 meV.

Al10Ti2的3个稳定结构可以归属于1个类型,即Al13正二十面体结构去掉1个原子所形成的,10c只发生了微小的形变,其点群对称性为Cs,10b是在9b的基础上又添加了1个Al原子,但是此Al原子并不在原来正二十面体的结构上,偏离了原来的五角环,其点群对称性同为Cs.10a就有了较大的形变,其底部的五角环没有完全封闭,有一个扩张的趋势,其点群对称性为C1,并且10a是在纯Al12团簇的基态结构上替换2个Al原子得到.10b和10c的能量差仅为6 meV.在正二十面体结构的Al13团簇上替换2个相对位置的Al原子得到11a,替换后的点群对称性为D5d,而11c是替换2个非中心不相邻的Al原子得到,其替换后的点群对称性将为Cs.11b相对于正二十面体结构有较大的改变,在Al12Ti团簇的12b结构上替换而成,其点群对称性为C2v.

从这些结构分析来看,在Aln+1Ti结构基础上1个Al原子被Ti原子替换后所得到优化模型的方式占据了主导地位.

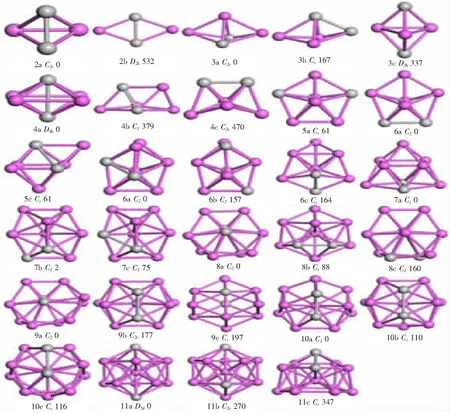
图1 Al12Ti2(n=2～11)团簇的稳定构型,其中灰色球代表Ti 原子 Fig. 1 The stable structure of Al12Ti2 (n=2～11) clusters, the gray spheres represent Ti atomsFig. 1 F is constant

2.2团簇的稳定性分析团簇的稳定性可以通过平均结合能,二阶差分能以及分裂能测定,这些性质的计算公式为

Eb(AlnTi2)=[nE(Al)+2E(Ti)-

E(AlnTi2)]/(n+2),

(1)

Δ2E(AlnTi2)=E(Aln-1Ti2)+

E(Aln+1Ti2)-2E(Aln-1Ti2),

(2)

Efra(AlnTi2)=E(Aln-1Ti2)+

E(Al)-E(AlnTi2).

(3)

其中E代表体系的总能量.

从图2可以看出,随着团簇尺寸n的增大,AlnTi2的平均结合能呈现一个较为明显的递增趋势,说明在生长过程中团簇可以不断地获得能量并且可以说明对于表面效应突出的小团簇而言,其束缚能收敛于块体材料的行为缓慢,Aln+2纯团簇和AlnTi团簇的平均结合能也在图中以作比较.其中纯Aln团簇的平均结合能按如下计算:

Eb=[nE(Al)-E(Aln)]/n,

而AlnTi的平均结合能按如下公式计算

Eb(AlnTi)=[nE(Al)+

E(Ti)-E(AlnTi)]/(n+1).

如图2所述,掺杂1个Ti原子后的团簇明显要比纯Aln团簇稳定,而掺杂2个Ti原子也比掺杂1个Ti原子的结构更加稳定,这就表明掺杂2个Ti原子在某种程度上更能提高团簇的稳定性.

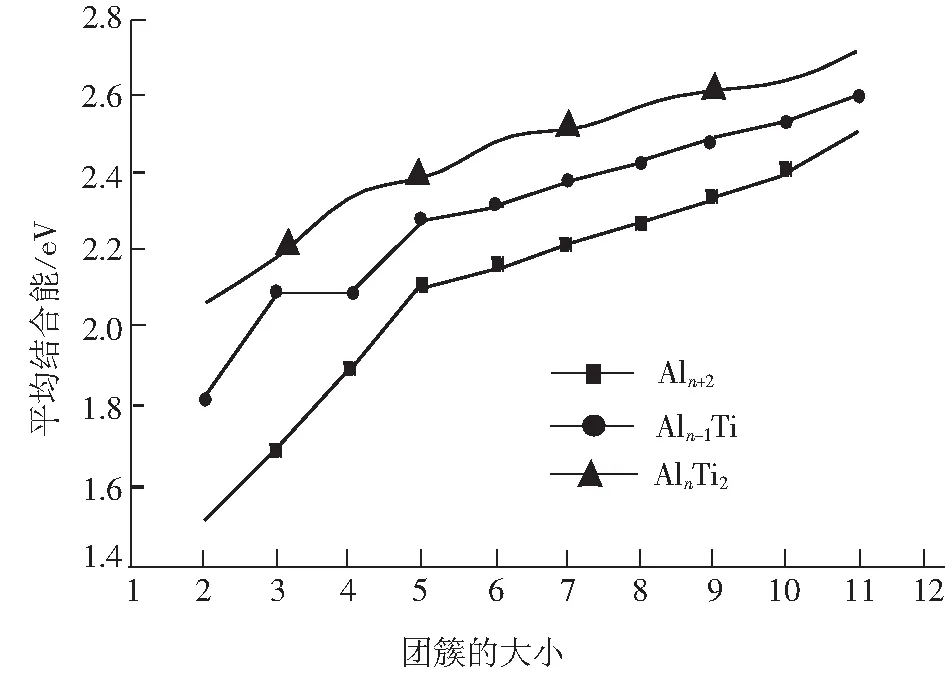
图2 Al12Ti2(n=2～11)的平均结合能以及与其对应的Aln+2和AlnTi团簇的平均结合能 Fig. 2 The average binding energies of Al12Ti2(n=2～11) clusters compared with that of Aln+2 and Aln+1Ti clusters

图3 Al12Ti2(n=2～11)的二阶差分能随团簇尺寸变化的规律 Fig. 3 The second order difference energies of Al12Ti2(n=2～11) clusters

二阶差分能代表着原子间的结合程度,能量二阶差分值越大,说明团簇稳定性越高,能量越小,则团簇的稳定性越差.图3给出了二阶差分能随着原子个数变化的规律.小尺寸掺杂团簇的稳定曲线往往存在一个明显的奇偶交替现象,AlnTi(n=3～12)就存在这样一个现象,在图3中可以看出,除了Al8Ti2团簇,能量变化也呈现出较为明显的奇偶交替现象,这一原因可能归结为团簇的结构问题,即由于Ti原子的掺杂,使得Al10或者Al9Ti团簇的结构发生较大的形变使得其结构对称性降低,从而影响稳定性.另一方面,当n=4,6,9时,团簇的二阶差分能值高于与其相邻的团簇,这说明与其相邻的团簇相比,Al4,6,9Ti2团簇具有较高的稳定性.

团簇物理中,分裂能是个更能敏感反映团簇稳定性的物理量,能量值越大团簇越稳定.图4给出了AlnTi2团簇的分裂能随着团簇尺寸变化的规律.从图中可以看出,与二阶差分能曲线相似,Al4,6,9Ti2团簇的分裂能具有区域极大值,这进一步表明Al4,6,9Ti2团簇较其相邻团簇更加稳定.

3 结论

在Dmol3程序包下,通过密度泛函理论中GGA/BP方法,对AlnTi2团簇进行结构优化,得出每个尺寸最稳定的3个模型,并对这些结构的演变过程进行分析,发现在Aln+1Ti团簇上替换1个Ti原子所形成的结构占主导地位.另外,通过计算平均结合能、二阶差分能以及分裂能分析团簇的稳定性.通过与Aln+2纯团簇以及Aln+1Ti掺杂团簇相比较,发现掺杂2个Ti原子之后的结构更加稳定.另外从二阶差分能和分裂能的曲线图中也可以看出Al4,6,9Ti2尺寸的团簇较其相邻团簇更稳定.

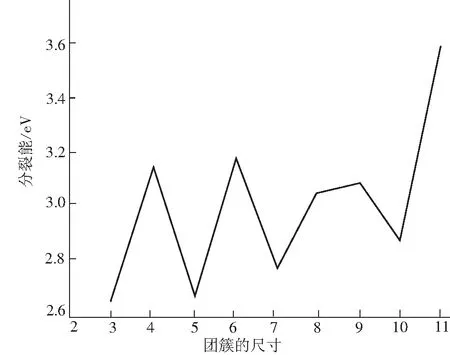
图4 Al12Ti2(n=2～11)的分裂能随团簇尺寸变化的规律 Fig. 4 The fragment energies of Al12Ti2(n=2～11) clusters

[1] Alonso J A. Electronic and atomic structure, and magnetism of transition-metal clusters[J]. Chem Rev,2000,100(2):637-678.

[2] Wang C C, Zhao R N, Han J G. Geometries and magnetisms of the Zrn(n=2～8) clusters: the density functional investigations[J]. J Chem Phys,2006,124(19):194301.

[3] Yin S, Moro R, Xu X, et al. Magnetic enhancement in cobalt-manganese alloy clusters[J]. Phys Rev Lett,2007,98:113401.

[4] 张萍,杨继先,汪勇. PdnAu(n=1～5)团簇的结构性质研究[J]. 四川师范大学学报:自然科学版,2008,31(2):328-331.

[5] 安芳芳,程新路. SiHn(n=1～4)和Si2Hn(n=2～6)的结构和光吸收谱第一性原理研究 [J]. 四川师范大学学报:自然科学版,2009,32(4):486-489.

[6] 吴位巍,张颂,岳莉,等. 合金团簇(PbSn)n(n=1～10)点偶极矩和极化率的理论研究 [J]. 四川师范大学学报:自然科学版,2013,36(5):741-744.

[7] Wang H Q, Kuang X Y, Li H F, et al. Density functional study of structural and electronic properties of bimetallic copper-gold clusters: comparison with pure and doped gold clusters[J]. Chem Phys,2010,12:5156-5165.

[8] Chuang F C, Wang C Z, Ho K H. Structure of neutral aluminum clusters Aln(2≤n≤23): genetic algorithm tight-binding calculations[J]. Phys Rev 2006,B73:125431(1-7).

[9] Sun J, Lu W C, Li Z S, et al. Appearance of the bulk motif in Al clusters[J]. J Chem Phys,2008,129:014707.

[10] Noya E G, Doye J P K, Calvo F. Theoretical study of the melting of aluminum clusters[J]. Phys Rev,2006,B73:125407.

[11] Gong X G, Sun D Y, Wang X Q. Atomic and electronic shells of Al7[J]. Phys Rev,2000,B62:15413-15416.

[12] Cox D M, Trevor D J, Whetten R L, et al. Aluminum clusters: magnetic properties[J]. J Chem Phys,1986,84:4651-4656.

[13] Deshpande M D, Kanhere D G, Vasiliev I. Ab initio absorption spectra of Aln(n=2～13)clusters[J]. Phys Rev,2003,B68:035428.

[14] Gong X G, Kumar V. Enhanced stability of magic clusters: A case study of icosahedral Al12X,X=B,Al,Ga,C,Si,Ge,Ti,As[J]. Phys Rev Lett,1993,70:2078.

[15] Kumar V, Sundararajan V. Ab initio molecular-dynamics studies of doped magic clusters and their interaction with atoms[J]. Phys Rev,1998,B57:4939-4942.

[16] Wang B L, Zhao J J, Shi D N, et al. Density-functional study of structural and electronic properties of AlnN(n=2～12) clusters[J]. Phys Rev,2005,A72:023204.

[17] Jiang Z Y, Yang C J, Li S T. Structures and stability of B-doped Al clusters: AlnB and AlnB2(n=1～7)[J]. J Chem Phys,2005,123(20):204315.

[18] Bergeron D E, Castleman Jr A W, Morisato T, et al. Formation of Al13I-: evidence for the superhalogen character of Al13[J]. Science,2004,304(5667):84-87.

[19] Bergeron D E, Roach P J, Castleman Jr A W, et al. Al cluster superatoms as halogens in polyhalides and as alkaline earths in lodide salts[J]. Science,2005,307(5667):231-235.

[20] Reddy B V, Khanna S N, Deevi S C. Electronic structure and magnetism in(FeAl)n(n≤6) clusters[J]. Chem Phys Lett,2001,333:465-470.

[21] Bailey M S, Wilson N T, Roberts C, et al. Structures, stabilities and ordering in Ni-Al nanoalloy clusters[J]. Eur Phys J D,2003,25:41-55.

[22] Wang M, Huang X W, Du Z L, et al. Structural, electronic, and magnetic properties of a series of aluminum clusters doped with various transition metals[J]. Chem Phys Lett,2009,480:258-264.

[23] Lang S M, Claes P, Neukermans S, et al. Cage structure formation of singly doped aluminum cluster cations AlnTM+(TM=Ti,V,Cr)[J]. J Am Soc Mass Spectrom,2011,22:1508-1514.

[24] Hua Y W, Liu Y L, Jiang G, et al. Geometric transition and electronic properties of titanium-doped aluminum clusters: AlnTi(n=2～24)[J]. J Phys Chem,2013,A117:2590-2597.

[25] Delley B. An all-electron numerical method for solving the local density functional for polyatomic molecules[J]. J Chem Phys,1990,92:508-517.

[26] Delley B. Analytic energy derivatives in the numerical local-density-functional approach[J]. J Chem Phys,1991,94:7245-7250.

[27] Delley B. From molecules to solids with the DMol3approach[J]. J Chem Phys,2000,113:7756-7764.

[28] Becke A D. A multicenter numerical integration scheme for polyatomic molecules[J]. J Chem Phys,1988,88:2547-2553.

[29] Perdew J P, Wang Y. Accurate and simple analytic representation of the electron-gas correlation energy[J]. Phys Rev,1992,B45:13244-13249.

[30] Pfrommer B G, Cote M, Louie S G, et al. Relaxation of crystals with the quasi-newton method[J]. J Comput Phys,1997,131(1):233-240.

[31] 沈吉梅,胡红星. 相对论效应对巯基金团簇电荷分布的影响[J]. 四川师范大学学报:自然科学版,2012,35(2):254-257.

[32] 冯胜奇. PdY4团簇:E⊗b1系统的Jahn-Teller效应及其能级分裂[J]. 四川师范大学学报:自然科学版,2011,34(3):370-375.

[33] 张福兰,徐伯华. C2Hx(x=4～6)在Co(111)表面吸附的理论研究[J]. 四川师范大学学报:自然科学版.2012,35(5):686-689.

[34] 周清,田斌. Cr掺杂BN半金属铁磁性的第一性原理计算[J]. 四川师范大学学报:自然科学版,2009,32(2):226-229.

[35] 文军,陈长乐. Nd掺杂ZnO薄膜的制备及室温光致发光研究[J]. 四川师范大学学报:自然科学版,2008,31(6):732-735.

[36] 吴艳南,吴定才,邓司浩,等. Co掺杂ZnO薄膜的结构及光磁性能研究[J]. 四川师范大学学报:自然科学版,2012,35(1):85-100.

[37] 董成军,徐明,周海平,等. Si掺杂InN的电子结构和光学性质的第一性原理计算[J]. 四川师范大学学报:自然科学版,2009,32(6):781-785.