高阶广义2D Ginzburg-Landau方程的随机吸引子

鲍 杰, 舒 级,2*

(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066; 2. 四川师范大学 可视化计算与虚拟现实重点实验室, 四川 成都 610066)

Ginzburg-Landau方程是耗散情形下的非线性Schrödinger方程,用于描述非平衡流体动力学的不稳定性以及超导体、非线性光学和Bose-Einstein凝聚等物理现象[1].

本文考虑D=[0,1]×[0,1]⊂R2中带加性噪声的高阶广义Ginzburg-Landau方程:

du=[-κu+χu+(γ1+iγ2)Δu-

(β1+iβ2)|u|2u-(δ1+iδ2)|u|4u-

(λ1+iλ2)|u|6u-(ν1+iν2)|u|2u-

(μ1+iμ2)u2

u(x,t)|∂D=0,

u(x,t0)=u0(x),

(1)

其中,χ>0,κ,γi,βi,δi,λi,νi,μi(i=1,2)均为实数.

此方程的确定性系统已有广泛研究.文献[2-3]讨论了不含7阶项方程的整体解的存在性和唯一性.文献[4]则讨论了不含5阶项时方程整体解的存在性.实际上关注的是确定性系统所忽略的许多微小扰动对系统的影响.该方程的渐近性质已由文献[5-8]分别讨论.文献[9]讨论了L2中附加了乘性噪声的随机广义Ginzburg-Landau方程的渐进行为.同时,还注意到无界域上带有可加白噪音的Ginzburg-Landau方程的随机吸引子已由文献[10]讨论.无穷维格系统上的随机Ginzburg-Landau方程的吸引子由文献[11]讨论.

吸引子是研究确定性动力系统长时间行为的有效工具,文献[12]中给出了详尽的描述.然而，当考虑随机因素，尤其是白噪声对系统的影响时，确定性系统所提供的工具显得无能为力.白噪声使得系统依概率1离开任何一个有界集.文献[13-14]提出了随机动力系统中随机吸引子的概念,并于文献[15]中系统阐述.随机吸引子实质上是紧的不变集，该不变集依概率并且随着时间变化.随机吸引子是对确定性系统中吸引子概念的推广，已应用于无穷维随机动力系统中[13-14,16].文献[15]深入讨论了文献[17]中的随机模型.近年来文献[6,18-19]使用先验估计的方法讨论了方程在有界区域情形下随机吸引子的存在性及其Hausdorff维数.文献[20-22]讨论了无界区间上随机微分方程吸引子的相关问题,文献[23-24]则关注了格上的随机动力系统的渐近性质.另一方面,带有动力学边值条件的随机微分方程已被讨论[25].文献[26]讨论了几类随机微分方程的不变流形的性质.本文的主要结果拓展了随机耗散偏微分方程一致先验估计的方法,并且证明方程在R上整体随机吸引子的存在性.显然，如同其在确定情形中所起的作用一样，此方法也适用于各种其他随机方程.

1 预备知识

本节给出有关随机动力系统的一些主要概念[13-15],并且给出随机吸引子存在性定理.

设(Ω,F,P)是一个概率空间.{θt:Ω→Ω,t∈R}是一族保测变换并且映射(t,ω)→θtω是可测的，θ0=id,θt+s=θtθs其中s,t∈R，则θt是一个流,相应的概率空间(Ω,F,P,θt)被称为可测的动力系统.进一步,假设θt是遍历变换.

定义1设(X,d)是Polish空间(包含具有可数基的局部紧的Hausdorff空间),F是σ-代数，θ是(Ω,F,P)对应的保测变换，则可测映射φ:R+×Ω×X→X,(t,ω,x)→φ(t,ω)x在X上P-a.s.满足:

(i)φ(0,ω)=id;

(ii)φ(t+s,ω)=φ(t,θsω)∘φ(s,ω),∀s,t∈R+(cocycle性质);

(iii)φ(t,ω):X→X连续,

就称φ是一个连续的随机动力系统.

定义2设(Ω,F,P)是概率空间，(X,d)是Polish空间，映射K:Ω→2X,{K(ω)}ω∈Ω是一族紧集,且对∀x∈X，映射ω→d(x,K(ω))依F可测，则称{K(ω)}ω∈Ω为随机紧集.

定义3设(Ω,F,P)是概率空间，(X,d)是Polish空间，φ是随机动力系统，A(ω)是随机集且有界集B⊂X，

(b) 如果随机集A(ω),P-a.s.满足:

(i) A(ω)是随机紧集,对∀ω∈Ω,A(ω)是紧的,并且对∀x∈X,映射x→dist(x,A(ω))可测;

(ii) A(ω)是不变集,即对t>0,φ(t,ω)A(ω)=A(θtω)；

(iii) A(ω)吸引所有的确定集合B⊂X,

在这一情况下,文献[13]的定理3.11推出如下关于随机吸引子存在性定理.

现在给出概率空间(Ω,F,P)的具体形式,令Ω={ω∈C(R,U)|ω(0)=0},其中U是一个Hilbert空间并满足L2(D)⊂U是一个Hilbert-Schmidt嵌入.方程(1)中的Wiener过程W为W(t)=ω(t),t∈R,ω∈Ω,P为Wiener测度.因此,可以在Ω上定义一族保测遍历变换(θt)t∈R，

θsω(t)=ω(t+s)-ω(s)， ∀t,s∈R，

从而(Ω,F,P,θt)就是遍历的可测随机动力系统.

2 z(t)的性质和方程的解产生的动力系统

du=[-κu+χu-(γ1+iγ2)Au-

(β1+iβ2)|u|2u-(δ1+iδ2)|u|4u-

(λ1+iλ2)|u|6u-(ν1+iν2)|u|2u-

(μ1+iμ2)u2

u(t0)=u0,

(2)

其中,κ,χ,γi,βi,δi,λi,νi,μi∈R(i=1,2),γ1,δ1,λ1,χ>0.

首先,给出如下带初值线性问题的解

dz=-(γ1+iγ2)Azdt+ΦdW(t),

(3)

初始条件为z(0)=0.文献[28]的定理6.10证明了z∈C[[0,∞),V]，并且对任意的t和s有

z(t,θsω)=z(t+s,ω), P-a.s.

(4)

根据文献[13-14]建立的方法，引进随机过程v=u-z.已知z是平稳过程并且其轨迹依概率P-a.e.连续.由方程(2)和v的形式知,随机过程v满足随机方程

(β1+iβ2)|u|2u-(δ1+iδ2)|u|4u-

(λ1+iλ2)|u|6u-(ν1+iν2)|u|2u-

(μ1+iμ2)u2z+χz,

(5)

v(t0,ω)=v0=u0-z(t0,ω).

(6)

方程(5)和(2)等价,对任一固定的随机参数ω,(5)是Random型方程.在假设γ1,δ1,χ>0成立且Φ:H→D(A)是线性算子的情况下,通过类似于文献[12]第4章定理5.1的证明,可以得到方程(5)和(6)解的性质如下(在P-a.s.的意义下):

(i) 对∀t0∈R,v0∈V，方程(5)和(6)存在唯一的解v∈C[[t0,T];V]∩C1([t0,T];V),∀T<∞;

(ii) 对∀t≥t0，映射v0=v(t0)→v(t,ω;t0,v0)从H到H是连续的;

(iii) 如果v0∈D(A),则v∈C[[t0,T];V]∩L2[[t0,T];D(A)]，∀T<∞.

用v(t,ω;t0,v0)表示(5)和(6)的解,则

u(t,ω;t0,u0)=v[t,ω;t0,u0-z(t0,ω)]+z(t,ω)

为方程(2)的解.令

φ(t,ω)u0=u(t,ω;t0,u0)=

v[t,ω;t0,u0-z(t0,ω)]+z(t,ω)，

则φ是对应于方程(2)的随机流.

3 随机吸引子

3.1先验估计

‖v[t,ω;u0-z(t0,ω)]‖2≤r12(ω),

t∈[t0,0], P-a.s.,

其中

g2在证明中给定.

证明令方程(5)与v在空间H上做内积,并取实部

Re(β1+iβ2)[|u|2u,v]-

Re(δ1+iδ2)[|u|4u,v]-

Re(λ1+iλ2)[|u|6u,v]-

Re(ν1+iν2)[|u|2u,v]-

Re(μ1+iμ2)(u2

Re[-κ(z,v)+χ(z,v)].

(7)

对(7)式右边的第2项应用Hölder不等式和Young不等式得

-Re(β1+iβ2)[|u|2u,v]=

-Re(β1+iβ2)[|v+z|2(v+z),v]≤

(8)

同样的方法处理(7)式右边的其他项,可得

(9)

(10)

-Reg((ν1+iν2)[|v+z|2(v+z),v]+

(μ1+iμ2)[(v+z)2

其中,ε4,ε5,ε6,ε7,C4均依赖于ν1,ν2,μ1,μ2.

对(7)式右边最后一项,同样有

Re[-κ(zx,v)+χ(z,v)]≤ε8(κ,χ)‖v‖2+C(κ,χ)[‖z‖2+‖z‖2].

(12)

接下来,联立(7)～(12)式,并选取参数εi(i=1,…,8)使其满足α=λ1-ε3>0,β=ε2-δ1,ε7=γ1/2,ε1+ε4+ε8=χ.并记μ=ε2+ε5,可得下列结果

(13)

其中

在t→∞时依P-a.s.至多以多项式形式增长[13].下文中出现的gi(i=2,…,9)与g1具有同样性质.

注意下面的式子:

其中g2(t)=2g1(t)+2Q2.

由Gronwall引理有

‖v(t)‖2≤2[‖u(t0)‖2+

‖z(t0)‖2]exp(-4χ(t-t0))+

最后，令

则引理得证.

引理2假设γ1>0,δ1>0,χ>0,Φ:H→D(A)是线性的.对t≤t0,其中t0由引理1给定,如下不等式成立:

ε11‖Δv‖2+ε12‖

(15)

其中

g4(t)=g3(t)+C4(β1,β2,δ1,δ2,λ1,λ2)×

其中g3(t)将在证明中给出.

证明令方程(5)与|v|6v在H中作内积

[∂tv,|v|6v]=-κ[v,|v|6v]+

χ[v,|v|6v]-(γ1+iγ2)[Av,|v|6v]-

(β1+iβ2)[|u|2u,|v|6v]-

(δ1+iδ2)[|u|4u,|v|6v]-

(λ1+iλ2)[|u|6u,|v|6v]-

(ν1+iν2)[|u|2u,|v|6v]-

(μ1+iμ2)[u2

[-κz+χz,|v|6v].

(16)

(16)式左端取实部为

(16)式右端第1项取实部得

(16)式右端第2项取实部得

下面处理(16)式右端第3项

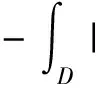
同时，应用如下等式

|(|v|2)|2+

将(16)右端第3项化为

-(γ1+iγ2)[Av,|v|6v]=

对(16)式右端第4,5,6项应用Hölder不等式和Young不等式可得

-Reg((δ1+iδ2)[|v+z|4(v+z),|v|6v]+

(λ1+iλ2)[|v+z|6(v+z),|v|6v]+

(β1+iβ2)[|v+z|2(v+z),|v|6v]g)≤

C4(β1,β2,δ1,δ2,λ1,λ2)×

C(‖v‖)‖

[-κz+χz,|v|6v]≤

-(ν1+iν2)[|u|2u,|v|6v]-

(μ1+iμ2)[u2

(-κz+χz,|v|6v)≤

ε11‖Δv‖2+ε12‖

ε11‖Δv‖2+ε12‖

(17)

‖

其中

证明方程(5)与Δv做内积,并关于x在[0,1]上积分,可得

(∂tv,Δv)=-κ(v,Δv)+χ(v,Δv)-

(γ1+iγ2)(Av,Δv)-(β1+iβ2)[|u|2u,Δv]-

(δ1+iδ2)[|u|4u,Δv]-

(λ1+iλ2)[|u|6u,Δv]-

(ν1+iν2)[|u|2u,Δv]-

(μ1+iμ2)[u2

(-κz+χz,Δv).

(18)

(18)式左端取实部得

(18)式右端第1,2,3项分别为：

-(γ1+iγ2)(Av,Δv)=γ1‖Δv‖2,

(18)式右端第4,5项应用Hölder不等式和Young不等式可得

-(β1+iβ2)[|u|2u,Δv]-

(δ1+iδ2)[|u|4u,Δv]≤

对(18)式右端第6项,为了与引理2的结果相一致,将其要分为两部分处理

-(λ1+iλ2)(|u|6u,Δv)≤

对不等式右端第1项应用引理2中使用过的等式

|(|v|2)|2+

则有

3v(|v|2)dx=

6iλ2((|v|2)+

λ1|

对不等式右端第2项应用Hölder不等式和Young不等式得

由此得到了(18)式右端第6项的估计:

-(λ1+iλ2)(|u|6u,Δv)≤

6iλ2((|v|2)+

λ1|

接下来用Hölder不等式和Young不等式来处理(18)式右端最后3项

Reg(-(ν1+iν2)[|u|2u,Δv]-(μ1+iμ2)[u2(-κz+χz,Δv)g)≤

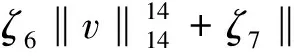
其中

g5(t)=c(ζ6,ζ7,ζ8,ν1,ν2,μ1,μ2,κ,χ)+

C(ζ8,κ,χ)[‖z(t)

C(ζ6,ζ7,ζ8,ν1,ν2,μ1,μ2,κ,χ)×

综合以上步骤可得(18)式:

-χ‖

ε13‖

6iλ2((|v|2)+

λ1|

(19)

其中

合并(17)和(19)式,可以得到如下形式的不等式:

-χ‖

(ε12δ2+ε13)‖

6i(λ2+γ2δ2)((|v|2)+

(λ1+γ1δ2)|

其中g7(t)=g4(t)+g6(t),δ是可以任意选择的正常数.上面不等式的积分是一个二次型,适当选取δ的值,使得矩阵

‖v‖2=(-Δv,v)≤

c‖Δv‖‖v‖≤r1(ω)‖Δv‖⟹

-χ‖

选择适当的ε11、ε12、ε13、ε14、δ使得以下不等式成立

(ε11δ2+ε14)‖Δv‖2+

(ε12δ2+ε13)‖

从而得到了所需要的不等式

(20)

其中g8(t)=g7(t)+C.由Gronwall引理,对于t0≤s≤t有

‖

当t=-1,s=t0时有

‖

exp(-γ1(-1-t0))+

exp(-γ1(-1-τ))dτ,

由于当t→-∞,g8(t)≥0至多以多项式形式增长,从而r2(ω)是P-a.s.有限的.

3.3H2中的吸收集

证明方程(5)与Δ2v在H上作内积并取实部得

-Re(β1+iβ2)[‖u‖2u,Δ2v]-

Re(δ1+iδ2)[‖u‖4u,Δ2v]-

Re(λ1+iλ2)[‖u‖6u,Δ2v]-

Re(ν1+iν2)[‖u‖2u,Δ2v]-

Re(μ1+iμ2)[u2

(-κz+χz,Δ2v).

(21)

根据

[|u|6u,Δ2v]=[|u|6u,Δ2u]-[|u|6u,Δ2z],

以及Hölder不等式和Young不等式有

-Re(β1+iβ2)[|u|2u,Δ2u]=

η1(β1,β2)[‖Δu‖2+‖

-Re(δ1+iδ2)[|u|4u,Δ2u]=

2|u|2u(

η2(δ1,δ2)(‖Δu‖2+‖

-Re(λ1+iλ2)[|u|6u,Δ2u]=

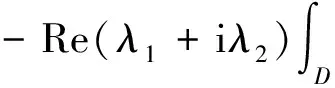
η3(λ1,λ2)(‖Δu‖2+‖

(21)式右端最后3项的估计分别为

-Re(ν1+iν2)[|u|2u,Δ2v]-

Re(μ1+iμ2)[u2

η4(ν1,ν2,μ1,μ2)×

(-κz+χz,Δ2v)≤η5(κ,χ)‖Δv‖2+

C(κ,χ)(‖Δz‖2+‖z‖2).

综上可得

η6‖Δv‖2+C(η1,η2,η3,η4)×

其中

g9(t)=C(η1,η2,η3,η4)×

C(κ,χ)(|Δz|2+|z|2).

选择适当参数，使得上式满足

χ‖Δv‖2+g9(t)+C(η1,η2,η3,η4)×

由Gronwall引理，对t0≤s≤t有

‖Δv(t)‖2≤‖Δv(s)‖2exp(-2χ(t-s))+

令t=-1,s=t0得

‖Δv(-1)‖2≤‖Δv(t0)‖2exp(2χ(1+t0))+

对上式中‖Δv‖2的有界性进行讨论:(18)式关于变量t在[-1,0]上取积分可得

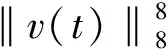
在第2节中已经知道随机广义Ginzburg-Landau方程产生随机动力系统S,由引理3和引理4知该随机动力系统存在紧吸收集,应用定理1即得到本文的主要结论.

定理2假设γ1>0,δ1>0,χ>0,Φ:H→D(A)是线性的,并且矩阵M是非负定的,则由随机Ginzburg-Landau方程(2)产生的随机动力系统在空间V中存在整体随机吸引子A(ω).

[1] Brand H R, Deissler R J. Interaction of localized solutions for subcritical bifurcations[J]. Phys Rev Lett,1989,63:2801-2804.

[2] 郭柏灵,高洪俊. 广义Ginzburg-Landau方程的有限维行为[J]. 自然科学进展,1994,4(4):423-434.

[3] Duan J, Holme P, Titi E S. Global existence theory for a generalized Ginzburg-Landau equation[J]. Nonlinearity,1992,5:1303-1314.

[4] Guo B, Wang X. Finite dimensional behavior for the derivative Ginzburg-Landau equation in two spatial dimensions[J]. Physica,1995,D89(1):83-99.

[5] Guo B, Wang G L, Li D L. The attractor of the stochastic generalized Ginzburg-Landau equation[J]. Sci China:Math,2008,A51:955-964.

[6] Li D L, Guo B. Asymptotic behavior of the 2D generalized stochastic Ginzburg-Landau equation with additive noise[J]. Appl Math Mech,2009,30(8):883-894.

[7] Li D L, Dai Z D, Liu X H. Long time behaviour for generalized complex Ginzburg-Landau equation[J]. J Math Anal Appl,2007,330:934-948.

[8] Wang G L, Guo B L, Li Y R. The asymptotic behavior of the stochastic Ginzburg-Landau equation with additive noise[J]. Appl Math Comput,2008,198:849-857.

[9] 王蕊,李扬荣. 带有可乘白噪音的广义Ginzburg-Landau方程的随机吸引子[J]. 西南大学学报:自然科学版,2012,34(2):92-95.

[10] 付颖,李扬荣. 无界域上带有可加白噪音的Ginzburg-Landau方程的随机吸引子[J]. 西南大学学报:自然科学版,2012,37(12):37-42.

[11] Zhao C D, Zhou S F. Limit behavior of global attractors for the complex Ginzburg-Landau equation on infinite lattices[J]. Appl Math Lett,2008,21:628-635.

[12] Temam R. Infinite-Dimensional Systems in Mechanics and Physics[M]. New York:Springer-Verlag,1988.

[13] Crauel H, Flaudoli F. Attractors for random dynamical systems[J]. Probability Theory and Related Fields,1994,100:365-393.

[14] Crauel H, Debussche A, Franco F. Random attractors[J]. J Dyn Diff Eqns,1997,9(2):307-341.

[15] Arnold L. Random Dynamical Systems[M]. Berlin:Springer-Verlag,1998.

[16] Debussche A. Hausdorff dimension of random invariant set[J]. J Math Pure Appl,1998,77:967-988.

[17] Liu D. Convergence of spectral method for stochastic Ginzburg-Landau equation by space-time white noise[J]. Commun Math Sci,2003,1(2):361-375.

[18] Zhang Q. Random attractors for a Ginzburg-Landau equaton with additive noise[J]. Chaos Soliton & Fract,2009,39:463-472.

[19] 杜先云,陈炜. 具有可加噪声的耗散KdV型方程的随机吸引子[J]. 四川师范大学学报:自然科学版,2012,35(5):651-655.

[20] Zhao C D, Zhou S F. Random attractor for stochastic reaction-diffusion equation with multiplicative noise on unbounded domains[J]. J Math Anal Appl,2011,384:160-172.

[21] P W Bates, Lu K N, Wang B X. Random attractors for stochastic reaction-diffusion equations on unbounded domains[J]. J Diff Eqns,2009,246:845-869.

[22] Sun C Y, Zhong C K. Attractors for the semilinear reaction-diffusion equation with distribution derivatives in unbounded domains[J]. Nonlinear Anal,2005,63(1):49-65.

[23] Wang X H, Li S Y, Xu D Y. Random attrcators for second-order stochastic lattic dynamical systems[J]. Nonlinear Anal,2010,72(1):483-393.

[24] Huang J H. The random attractor of stochastic FitzHugh-Nagumo equations in an infinite lattice with white noises[J]. Physica D:Nonlinear Phenomena,2007,233(2):83-94.

[25] 陈光淦. 一类带动力边值的随机抛物型偏微分方程的不变叶理[J]. 四川师范大学学报:自然科学版,2012,35(1):137-142.

[26] Chen G, Duan J, Zhang J. Geometric shape of invariant manifolds for a class of stochastic partial differential equations[J]. J Math Phys,2011,52(7):07270201-07270214.

[27] Crauel H. Global random attractors are uniquely determined by attracting deterministic compact set[J]. Ann Math Pure Appl,1999,176:57-72.

[28] Da Prato G, Zabczyk J. Stochastic Equations in Infinite Dimensions[M]. Cambridge:Cambridge University Press,1992.