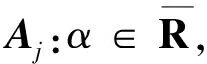Max-plus代数中analogy-transitive矩阵及其本征问题

王绘莉, 舒乾宇, 王学平

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

多机器交互生产过程是一类较为典型的管理应用.当该过程是多步生产问题时,描述该系统的定态问题即为max-plus代数上矩阵的本征问题.一般情况下,解决这类本征问题的算法大小为O(n3)[1].继文献[1]之后,max-plus代数上矩阵的本征问题被很多学者关注并深入研究.特别地,对于一些特殊形式的矩阵,计算本征问题的算法复杂度较一般情况有所降低[5-14].因此从降低算法复杂度的角度考虑研究特殊矩阵的本征问题是有重大意义的.P. Butkovicˇ等[5]给出一个O(n2)的算法计算双值矩阵的极大圈平均.M. Gavalec等[6]给出一个O(n2)的算法计算Monge矩阵的极大圈平均.J. Plavka[7-9]讨论了循环矩阵的本征问题、Monotone-Toeplitz矩阵的本征问题和l-parametric本征问题.K. Cechlrov[10]研究了interval矩阵的本征向量问题.随后M. Gavalec等[11]给出能够计算出Monge矩阵的一个本征向量的算法.M. Gavalec等[12]给出最快解决极值双参数本征问题的算法.

本文在max-plus代数上讨论一类特殊的矩阵,即analogy-transitive矩阵.首先讨论analogy-transitive矩阵的基本性质,给出判定一个矩阵是否为analogy-transitive矩阵的判定定理及算法,其算法复杂度为O(n2).其次讨论该类矩阵的极大圈平均问题、本征值本征向量问题.

1 预备知识

如果A是一个方阵,则A的k次幂记作Ak,且

Ak=A⊗Ak-1,

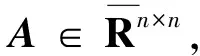
接下来基于文献[5]给出一些基本概念及符号说明.设n是一个正整数,Mn表示所有阶为n的实矩阵的集合.Σ表示N={1,2,…,n}的子集的循环置换集(Σ中的元素称为基本圈).设A=(aij)∈Mn,σ∈Σ,σ=(i1,…,ik),σ的权ω(σ,A)=ai1i2+ai2i3+…+aiki1,其中k称为σ的长度,记作l(σ).进一步定义

(1)

λ(A)表示A的极大圈平均,即

(2)

由于Nc(A)中的元素在本征问题中有非常重要的作用,因此称为A的关键结点或本征结点.如果μ(σ,A)=λ(A),则σ称为DA中的关键圈.如果i,j∈Nc(A)属于同一个关键圈,则称i、j是等价的,记作i～j,否则称作是不等价的,记作ij.显然～构成一个在Nc(A)上的等价关系.A的关键图C(A)由A的关键圈所在的弧及结点集N构成.

定理1.1[1]设A∈Mn,则λ(A)是A的唯一本征值.

找本征值λ(A)的问题已得到许多学者的广泛讨论,且给出不同的算法,其中较经典的是1978年由Karp给出的大小为O(n3)的算法.

设矩阵B∈Mn,记Δ(B)=B⊕B2⊕…⊕Bn.令Aλ=(λ(A))-1⊗A,文献[1]证明了矩阵Δ(Aλ)至少包含一个对角线元素为0的列向量,且每一个这样的列向量都是A的本征向量,称为基本本征向量.易知每一个基本本征向量的线性组合也是一个本征向量.

记Δ(Aλ)=(γij)的列向量为g1,…,gn.由Δ(Aλ)的定义知γij表示DAλ中从i到j的最重路的权.利用Floyd-Warshall算法,计算Δ(Aλ)需O(n3)步.因此找出Δ(Aλ)的列向量中所有的基本本征向量至多需要O(n3)步.由于A∈Mn,由定理2.1知λ(A)是A的唯一本征值,因此A的所有本征向量都对应于本征值λ(A).记A的所有本征向量的集合为V(A),称为A的本征空间,V(A)的维数记为pd(A).由以下2个定理易知pd(A)等于C(A)的关键分支的个数,或者等于由A的所有基本本征向量所构成的矩阵的列向量空间的任意一个基的基数.已知计算一个矩阵的列向量空间的基的算法大小为O(n3)[15],那么计算pd(A)也需O(n3)步.

引理1.1[15]设A∈Mn,如果x=(x1,…,xn)T∈V(A),则

⊗gj.

定理1.2[1]设A∈Mn,如果i,j∈Nc(A),则存在某个α∈R使得gi=α⊗gj当且仅当i～j.

定理1.3[1]设A∈Mn,则

定理1.4[16]设A∈Mn,则V(A)是一个非平凡子空间且从(Nc(A),～)的每一个等价类中恰好取出一个向量gk便构成V(A)的一个基.

2 Analogy-transitive矩阵

性质2.1设A=(aij)为n阶analogy-transitive矩阵,则有

(i)∀i∈N,aii=0;

(ii)∀1≤i,j≤n,aij=-aji.

证明(i) ∀i∈N,由analogy-transitive矩阵的定义有aii+aii=aii,即2aii=aii,则aii=0;

(ii)若i=j,则由(i)的证明知aii=-aii=0.若i≠j,则由analogy-transitive矩阵的定义及(i)有aij+aji=aii=0,即aij=-aji.

如果一个矩阵是analogy-transitive矩阵,则称这个矩阵具有analogy-transitive性质.由analogy-transitive矩阵的定义及性质,给出一个判定analogy-transitive矩阵的充分必要条件.

定理2.1A=(aij)∈Mn是analogy-transitive矩阵当且仅当

(i)∀i∈N,aii=0;

(ii)∀i,j∈N,i≠j,aij=-aji;

(iii)∀2≤i

证明必要性已知A=(aij)∈Mn是analogy-transitive矩阵,则由性质2.1知(i)、(ii)成立.由定义2.1,∀i,j∈N,有a1i+aij=a1j,即aij=a1j-a1i.

充分性由定义2.1,只需证明∀i,j,k∈N,aik+akj=aij成立.以下分4种情况进行证明.

1)当i=j=k时,则由(i)有aii+aii=aii=0.

2)当i=k≠j或i≠j=k时,不妨设i=k≠j,则aii+aij=0+aij=aij;当i≠j=k时同理可证.

3)当i=j≠k时,由(i)、(ii)有aik+aki=aik-aik=0=aii.

4)当i、j、k互不相等时,若i=1,不妨设ki>1,则ai1+a1j=a1j-a1i=aij.

若i、j、k均不等于1,不妨设i

综上,∀i,j,k∈N,aik+akj=aij成立.

由以上的analogy-transitive矩阵判定定理易知,任意1个analogy-transitive矩阵的所有元素只需由a12,a13…,a1n这n-1个元素完全刻画,且刻画是唯一的.反过来,任意1个n-1维实向量x=(x1,x2,…,xn-1),令a12=x1,a13=x2,…,a1n=xn-1,则由判定定理中的(i)～(iii)可知a12,a13…,a1n可唯一确定1个analogy-transitive矩阵的所有元素,即n-1维实向量与analogy-transitive矩阵一一对应.

事实上analogy-transitive矩阵的判定定理提供了一种判断一个矩阵是否为analogy-transitive矩阵的算法.

定理2.2设A=(aij)∈Mn,存在一种检验A是否具有analogy-transitive性质的算法,算法复杂度为O(n2).

3 Analogy-transitive矩阵的本征问题

定理3.1设A=(aij)∈Mn是analogy-transitive矩阵,则λ(A)=0.

证明设DA中任意长度大于等于2的圈σ=(i1,i2,…,il,i1)(l≥2),

ω(σ,A)=ai1i2+ai2i3+ai3i4…+ail-1il+aili1=

ai1i3+ai3i4…+ail-1il+aili1=

ai1i4+…+ail-1il+aili1=

⋮

ai1i1=0,

因此得

再考虑所有自环∀i∈N,aii=0,则

λ(A)=0.

命题3.1设A=(aij)∈Mn是analogy-transitive矩阵,则A2=A.

证明A是analogy-transitive矩阵,则∀i,j,l∈N,aik+akj=aij.因此

即A2=A.

定理3.2设A=(aij)∈Mn是analogy-transitive矩阵,则本征空间V(A)={α⊗Aj:α∈R,∀j∈N}.

证明对于analogy-transitive矩阵,λ(A)=0是其唯一的本征值,则Aλ=A,因此Δ(Aλ)=A⊕A2⊕…⊕An,由命题3.1有A2=A,则Δ(Aλ)=A.接下来找出Δ(Aλ)中对角线元素为0的列向量.由analogy-transitive矩阵的定义知∀i∈N,aii=0,即Nc(A)=N且Δ(Aλ)=A中所有列向量都是A的本征向量.再由analogy-transitive矩阵的定义,对于1≤i,j≤n,且i≠j,有alj=ali+aij,∀l∈N,即Aj=aij⊗Ai,也即gj=aij⊗gi,由定理1.2,i～j,即关键结点集Nc(A)关于“～”有且仅有1个等价类.因此对于1个analogy-transitive矩阵,其本征空间为

由定理3.2的证明易知1个analogy-transitive矩阵A的本征空间的基为

{Aj:j∈N},

即pd(A)=1.

定理3.3设A=(aij)∈Mn是analogy-transitive矩阵,则存在一个算法计算出A的本征值及所有本征向量,算法复杂度为O(n2).

[1] Cuninghame-Green R A. Minimax Algebra[M]. New York:Springer-Verlag,1979.

[2] Cuninghame-Green R A. Minimax Algebra and Applications[J]. Adv in Imaging and Electron Physics,1995,90:1-121.

[3] Gondran M, Minoux M. Linear algebra of dioïds: a survey of recent results[J]. Ann Discrete Math,1984,19:147-164.

[4] Zimmermann U. Linear and combinatorial optimization in ordered algebra structures[J]. Ann Discrete Math,1981,10:379.

[5] Butkovicˇ P, Cuninghame-Green R A. AnO(n2) algorithm for the maximum cycle mean of ann×nbivalent matrix[J]. Discrete Appl Math,1992,35:157-163.

[6] Gavalec M, Plavka J. AnO(n2) algorithm for maximum cycle mean of Monge matrices in max-algebra[J]. Discrete Appl Math,2003,127:651-656.

[7] Plavka J. On eigenproblem for circulant matrices in max-algebra[J]. Optimization,2001,50:477-483.

[8] Plavka J. Eigenproblem for monotone and toeplitz matrices in a max-algebra[J]. Optimization,2003,53:95-101.

[9] Plavka J. L-parametric eigenproblem in max algebra[J]. Discrete Appl Math,2005,150:16-28.

[11] Gavalec M, Plavka J. Computing an eigenvector of a monge matrix in max-plus algebra[J]. Math Methods Operation Research,2006,62:543-551.

[12] Gavalec M, Plavka J. Fast algorithm for extremal biparametric eigenproblem[J]. Acta Electrotechnica et Informatica,2007,7:23-27.

[13] Cuninghame-Green R A, Butkovicˇ P. Extremal eigenproblem for bivalent matrices[J]. Linear Algebra and Its Appl,1995,222:77-89.

[14] Plavka J. Static maximum cycle mean problem of a trivalent matrix[J]. Optimization,1996,37:171-176.

[15] Butkovicˇ P. Max-linear Systems: Theory and Algorithms[M]. London:Springer-Verlag,2010.

[16] Akian M, Gaubert S, Walsh C. Discrete max-plus spectral theory[J]. Idempotent Mathematics and Mathematical Physics,2005,377:53-77.

[17] Butkovicˇ P, Schneider H, Sergeev S. Generators, extremals and bases of max cones[J]. Linear Algebra and Its Applications,2007,421(2):394-406.

[18] Butkovicˇ P. Max-algebra: the linear algebra of combinatorics?[J]. Linear Algebra and Its Applications,2003,367:313-335.

[19] Butkovicˇ P, Zimmermann K. A strongly polynomial algorithm for solving two-sided linear systems in max-algebra[J]. Discrete Appl Math,2006,154(3):437-446.

[20] Butkovicˇ P, Cuninghame-Green R A, Gaubert S. Reducible spectral theory with applications to the robustness of matrices in max-algebra[J]. SIAM J Matrix Anal Appl,2009,31(3):1412-1431.

[21] Butkovicˇ P, Lewis S. On the job rotation problem[J]. Discrete Optimization,2007,4(2):163-174.

[22] Burkard R E, Butkovicˇ P. Max algebra and the linear assignment problem[J]. Math Programming,2003,98(1/2/3):415-429.

[23] Cuninghame-Green R A, Butkovicˇ P. Discrete-event dynamic systems: the strictly convex case[J]. Ann Operations Research,1995,57(1):45-63.

[24] Butkovic P. On properties of solution sets of extremal linear programs[J]. Ann Discrete Math,1984,19:41-54.

[25] Butkovic P, Gaubert S. Sign-nonsingular matrices and matrices with unbalanced determinant in symmetrised semirings[J]. Linear Algebra and Its Applications,1999,301:195-201.

[26] Butkovic P. Simple image set of (max,+) linear mappings[J]. Discrete Applied Mathematics,2000,105:73-86.

[27] Butkovic P, MacCaig M. On integer eigenvectors and subeigenvectors in the max-plus algebra[J]. Linear Algebra and Its Applications,2013,438:3408-3424.

[28] Butkovic P, MacCaig M. On the integer max-linear programming problem[J]. Discrete Applied Mathematics,2014,162:128-141.