首次积分法下高维非线性偏微分方程新的行波解
黄 欣
(1. 四川财经职业学院 基础部, 四川 成都 610101; 2. 四川师范大学 数学与软件科学学院, 四川 成都 610066)
非线性波现象有很多,如色散、耗散、反应和对流等,它们出现在离子体物理、固体物理、流体力学、光学纤维等各类科学领域中.非线性现象常常与非线性偏微分方程联系紧密,比如在地震研究中,地震波可以用非线性偏微分方程描述,又可以用环孤粒子或者是环孤立波来描述;台风一些非常重要的结构特征可以通过二维的Euler方程来描述;易引发极端气候的大气阻塞现象可以用KdV孤立子来描述.因此在研究非线性现象的过程中,关于非线性偏微分方程的研究占到了一个重要的角色.人们把目光集中到了求这些对应非线性发展方程的精确解[1-8]上,因为这些解正是揭示各类非线性现象的重要工具,为得到这些非线性发展方程的精确解,许多直接的方法被提出,包括齐次平衡法[9]、双曲正切法[10]、Exp-函数法[11]、广义Riccati方程法[12]等.
首次积分法是求解非线性波动方程的有效方法之一,于2002年由Z. S. Feng[13]在求解Burgers-KdV方程中提出.其基本思想是利用行波变换将非线性偏微分方程转化为常微分方程,再构造出这个常微分方程的一个首次积分,由此就可以把此常微分方程变成一个一阶可积的常微分方程组,通过直接积分的办法求解此常微分方程组,进而得到原方程的精确解.目前这个方法已经被成功的广泛应用于各种非线性发展方程中,比如Fisher方程[14]、非线性Schrödinger方程[15]、Gardner方程[16]等.
本文考虑如下(3+1)维修正KdV-Zakharov-Kuznetsev方程
ut+αu2ux+uxxx+uxyy+uxzz=0,
(1)
其中α为实常数.文献[17]用(G′/G)-展开法获得了方程(1)的精确解,文献[18]用Exp-函数法研究了此方程.本文将通过首次积分法和符号运算系统Mathematica研究(3+1)维修正KdV-Zakharov-Kuznetsev方程(1),并得出了方程的新精确解.
1 首次积分法
对于给定的非线性偏微分方程
P(u,ut,ux,uxx,utt,uxt,…)=0,
(2)
假设方程存在行波解
u=u(ξ),ξ=x-ct,
其中c表示波速,则原方程就变为
P(u,u′,u″,…)=0.
(3)
再令
X(ξ)=u(ξ),Y(ξ)=u′(ξ),
(4)
则方程(3)等价于常微分方程组
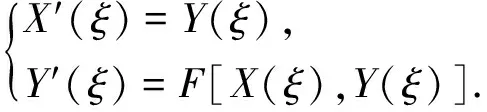
(5)
通过常微分方程的定性理论[19]可知,对于常微分方程组(5),若能找到其2个首次积分,就能直接获得其通解,但一般说来,由于没有系统的构造首次积分的理论,即使想要获得一个首次积分都很困难.Z. S. Feng[13]提出的首次积分法用到了代数环论中的除法定理[20],使得目标常微分方程组(5)能够转化为一阶可积的常微分方程,通过转换之后的方程有很多方法可以比较容易处理求解问题.
除法定理假设P(w,z)、Q(w,z)都是定义在复数域C[w,z]上的多项式,并且多项式P(w,z)在复数域C[w,z]上是不可约的.如果多项式Q(w,z)不包含多项式P(w,z)的所有零点,则复数域C[w,z]上必定存在一个多项式G(w,z),使得
Q(w,z)=P(w,z)·G(w,z).
2 (3+1)维修正KdV-Zakharov-Kuznetsev方程的精确解
假设方程(1)有如下形式的行波解
u(x,y,z,t)=u(ξ),ξ=x+y+z-ct,
(6)
其中c为待定参数.将(6)式带入(1)式得
-cu′+αu2u′+3u‴=0,
(7)
将(7)式积分一次,并令积分常数为0,可得
(8)
令X(ξ)=u(ξ),Y(ξ)=u′(ξ),则方程(8)等价于
(9)
按照首次积分法的步骤,假定X(ξ)和Y(ξ)是方程组(9)的非平凡解,则方程组(9)的首次积分为
其中ai(X(ξ))(i=0,1,…m)是X(ξ)的多项式,am(X(ξ))≠0.根据除法定理可知,在复数域C上会有
q(X(ξ),Y(ξ))=g(X(ξ))+h(X(ξ))Y(ξ),
使得
仅考虑(11)式中的2种情况,即假定m=1和m=2.
情形1假定m=1,则有
p(X,Y)=a0(X)+a1(X)Y,
(12)
代入(11)式后比较两边Yi(i=2,1,0)的系数得
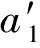
(13)
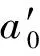
(14)
因为ai(X)(i=0,1)为多项式,则从(13)式可知a1(X)为常数,且h(X)=0.为运算的简便,不妨取a1(X)=1,通过平衡a0(X)和g(X)的系数,可以得出deg[g(X)]=1,相应的deg[a0(X)]=2.
假定
g(x)=A1X+B0,A1≠0,
则有
(16)
其中A0为积分常数.
李离愀然不乐:“我父亲说,龙化为鱼,十年为期,意思是长安城不出十年,就会被叛军打破,你说到那个时候,写这首诗的吏部郎中王维大人,会不会降?”
将(16)式代入(15)式并比较两边Xi的系数可得
将(17)式代入(10)式得
(19)
将(19)式代入(9)式中,即可得(9)式的精确解,故原方程的精确解为
(20)
其中ξ0为任意常数.同理将(18)式代入(10)式得
(21)
将(21)式代入(9)式中,即可得(9)式的解,故原方程的精确解为
(22)
其中ξ0为任意常数.
情形2假定m=2,则有
p(X,Y)=a0(X)+a1(X)Y+a2(X)Y2, (23)
通过比较方程两边Yi的系数,可得
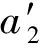
(24)
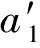
(25)
=g(X)a1(X)+h(X)a0(X),
(26)
(27)
因为ai(X)(i=0,1)为多项式,则从(24)式可知a2(X)为常数,且h(X)=0.为运算简便,不妨取a2(X)=1,平衡a0(X)、a1(X)、g(X)的系数,可以得出deg[g(X)]=1.
假定
g(X)=A1X+B0A1≠0,
则可得a1(X)和a0(X)为
(28)
(29)
其中D为积分常数.
将a0(X)、a1(X)、g(X)代入(27)式, 令Xi的同次幂系数为0,则可以得到一个系统的非线性代数方程组,借助符号计算系统Mathematica解此方程可得
(30)
将(30)式代入(10)式可得
(31)
将(31)式代入(9)式,可得(9)式的解,故(3+1)维修正KdV-Zakharov-Kuznetsev方程的精确解为
u(x,y,z,t)=
其中ξ0为任意常数.
3 结论和展望
在交换代数环论的基础上,运用首次积分法,借助符号计算系统Mathematica,本文对(3+1)维修正KdV-Zakharov-Kuznetsev方程进行了研究,获得了该方程的精确行波解,这些解均为新解.下一步, 打算对此方法进行改进,使其可以往高阶的、高维的非线性波动方程上推广研究,此外还准备结合分岔理论,结合相图,分析行波解的特性.
[1]Guo B L, Ling L M. Rogue wave, Breathers and Bright-Dark-Rogue solutions for the coupled Schrödinger equations[J]. Chinese Phys Lett,2011,28:110202.
[2]Guo B L, Ling L M, Liu Q P. Nonlinear Schrödinger equation: generalized Darboux transformation and rogue wave solutions[J]. Phys Rev,2012,E85:026607.
[3]Guo B L, Ling L M, Liu Q P. High-order solutions and generalized Darboux transformations of derivative nonlinear Schrödinger equations[J]. Stud Appl Math,2013,130:317-344.
[4]邓艳萍,周钰谦. 非线性Schrödinger方程组初值问题的驻波解[J]. 四川师范大学学报:自然科学版,2013,36(2):243-246.
[5]刘倩,周钰谦,刘合春. 广义Hirota-Satsuma耦合KdV方程的精确解[J]. 四川师范大学学报:自然科学版,2011,34(3):335-339.
[6]Ling L M, Liu Q P. A long waves-short waves model: Darboux transformation and soliton solutions[J]. J Math Phys,2011,52:053513.
[7]Huang X. The investigation of solutions to the coupled Schrödinger-Boussinesq equations[J]. Abstr Appl Anal,2013,2013:170372.
[8]Huang X, Guo B L, Ling L M. Darboux transformation and novel solutions for the long wave-short wave model[J]. J Nonl Math Phys,2013,20:514-528.
[9]Wang M L, Zhou Y B, Li Z B. Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J]. Phys Lett,1996,A216:67-75.
[10]Fan E G. Extended tanh-function method and its applications to nonlinear equations[J]. Phys Lett,2000,A277:212-218.
[11]Shin B C, Darvishi M T, Barati A. Some exact and new solutions of the Nizhnik-Novikov-Vesselov equation using the exp-function method[J]. Comput Math Appl,2009,58:2147-2151.
[12]Yan Z Y, Zhang H Q. New explicit solitary wave solutions and periodic wave solutions for Whitham-Broer-Kaupequation in shallow water[J]. Phys Lett,2001,A285:355-362.
[13]Feng Z S. The first integral method to study the Burgers-Korteweg-de Vries equation[J]. Phys Lett,2002,A35:343-349.
[14] Raslan K R. The first integral method for solving some important nonlinear partial differential equations[J]. Nonlinear Dynamics,2008,53:281-286.
[15] Taghizadeh N, Mirzazadeh M, Farahrooz F. Exact solutions of the nonlinear Schrödinger equation by the first integral method[J]. J Math Anal Appl,2011,374:549-553.
[16]Taghizadeh N, Mirzazadeh M, Farahrooz F. New exact solutions of some nonlinear partial differential equations by the first integral method[J]. Appl Appl Math,2010,5(10):446-456.
[17]Zayed E M E. Traveling wave solutions for higher dimensional nonlinear evolution equations using the (G′/G)-expansion method[J]. Appl Math Informatics,2010,28:383-395.
[18]Naher H, Abdullah F A, Akbar M A. New traveling wave solutions of the higher dimensional nonlinear partial differential equation by the exp-function method[J]. J Appl Math,2012,2012:575387.
[19]丁同仁,李承治.常微分方程教程[M]. 2版. 北京:高等教育出版社,2004.
[20]Bourbaki N. Commutative Algebra[M]. Paris:Herman,Publishers in Arts and Science,1972.

