基于膨胀和腐蚀的迭代优化算法

蒲 石, 龙文光,2*

(1. 内江师范学院 现代教育技术中心, 四川 内江 641100; 2. 内江师范学院 计算机科学学院, 四川 内江 641100)

膨胀和腐蚀是数学形态学中最重要的2个基本操作,也是开、闭等其他操作的基础.当图像和结构元素比较大时,膨胀和腐蚀操作是非常耗时的,其时间复杂度为O(n4).因此,如何优化这2种运算一直是研究的热点问题[1-4].

根据公开的文献资料,膨胀和腐蚀的优化方法可以分为两大类.第一类方法根据链式法则将一个大的结构元素分解成为一系列较小的结构元素.许多学者提出了各自的优化算法.X. Zhuang等[3]提出了一种树形搜索算法,算法能将任意的结构元素分解成只包含2个像素的结构元素.X. Xu[4]提出的优化算法能将凸结构元素分解成3×3的结构.H. Park等[5]提出一种分解凸结构元素的优化算法,该算法可以快速的并发执行.R. F. Hashimoto等[6]提出一种可分离的、对称的凸结构元素模版.X. Zhuang[7]等发展了一种组合的优化技术,实现了对结构元素的连续分解.如果这种分解存在,该方法的性能可以达到或超过文献[3-5]的性能.其他的一些作者[8-13]也提出了一些分解算法,但这些算法都局限于凸或其他形状的结构元素.文献[11]提出一种能将任意形状的结构元素分解成3×3结构的分解算法,但一般而言,并不是所有的结构元素都有这样的一系列分解[4,7,11].此外,文献[10]的研究表明,通用的形态学模版分解问题是一个NP-complete问题.因此,结构元素分解方法适合离线的应用和小图像问题.第二类方法将结构元素看作一个整体而不进行分解[14].和第一类方法相比,这类方法适合任何一种简单连接的结构元素和在线应用[15-17].

本文提出一种基于第二类方法的改进膨胀和腐蚀迭代优化算法.通过定义结构元素的边界,一个简单连接的结构元素可以被看成由边界和内部点组成.在改进的优化算法中,膨胀和腐蚀操作被定义为一系列的迭代操作以降低算法时间复杂度.

1 基本概念

定义P∈Rv×w和S∈Rm×n分别是二值图像和结构元素,(x,y)表示一个像素.假设S的左上角像素为(0,0),那么可以定义以下概念.

定义1如果集合Sup满足以下条件

Sup={(x,y)|(x,y)∈

S∩(x,y-1)∉S},

(1)

那么Sup是S的上边界.

定义2如果集合Slow满足以下条件

Slow={(x,y)|(x,y)∈

S∩(x,y+1)∉S},

(2)

那么Slow是S的下边界.

定义3如果集合Sleft满足以下条件

Sleft={(x,y)|(x,y)∈

S∩(x-1,y)∉S},

(3)

那么Sleft是S的左边界.

定义4如果集合Sright满足以下条件

Sright={(x,y)|(x,y)∈

S∩(x+1,y)∉S},

(4)

那么Sright是S的右边界.

定义5如果集合Sinner满足以下条件,

Sinner={(x,y)|(x,y)∈S∩((x,y)∉

(Sup∪Slow)∪(x,y)∉(Sleft∪Sright))},

(5)

那么Sinner是S的内部点.

以上定义中,定义5是由定义1和定义2,或定义3和定义4确定的.也就是说,定义5是一个相对概念,即使对于同一个S,由Sup和Slow确定的Sinner也可能和由Sleft和Sright确定的Sinner不同.

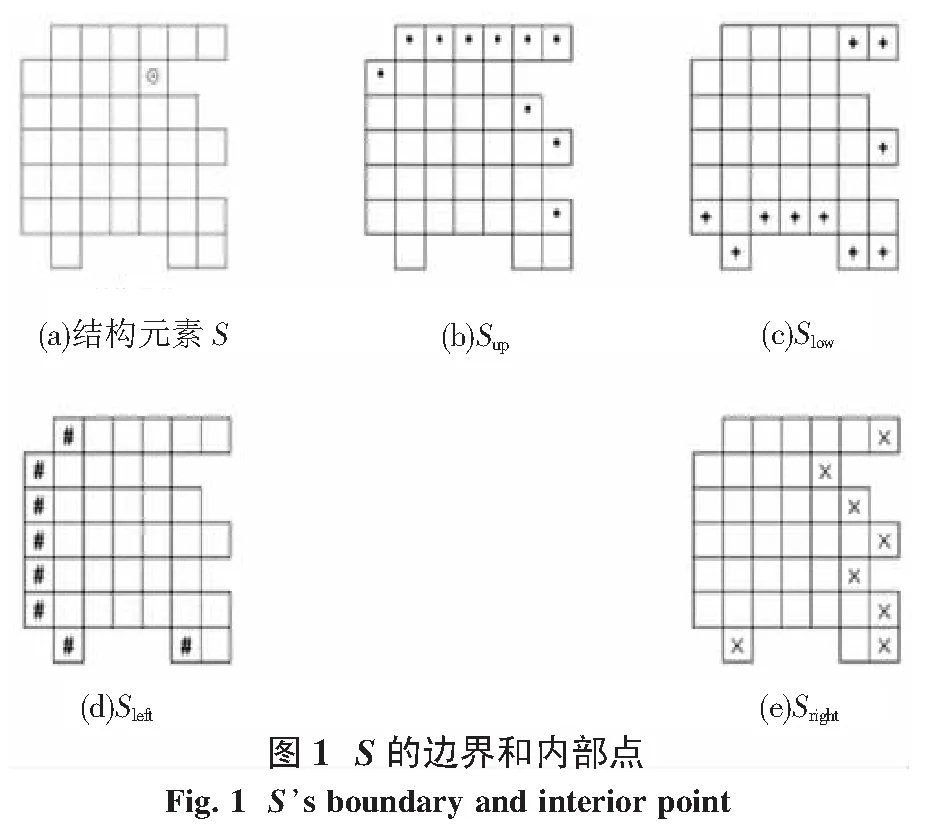
图1给出了关于以上概念的一个例子.图1(a)是一个任意形状的结构元素S,根据图1(b)和(c)中分别定义的左、右边界,用“⊙”标记的点属于Sinner.但是,根据图1(d)和(e)中分别定义的上、下边界,这个带“⊙”标记的点不属于Sinner.图1所示的例子说明Sinner是一个由边界确定的相对概念.此外,图1(d)和(e)还表明(x,y)可能同时属于Sup和Slow,或同时属于Sleft和Sright.

2 一种边界检测算法和时间复杂度

定义了边界和内部点的概念后,接下来的问题是如何检测边界.因为Sinner是一个相对概念,显然,Sup和Slow,或Sleft和Sright应该同时检测.以检测Sup和Slow为例,边界检测算法定义如下.

输入：任意形状的结构元素S.

步骤1选择S中一个未处理的列.

步骤2自上而下扫描当前列,如果相邻2个点的值发生了变化,例如(x,y-1)和(x,y),记录下所有这样的相邻点.

步骤3如果(x,y)的值为1,那么(x,y)∈Sup.

步骤4如果(x,y-1)的值为1,那么(x,y-1)∈Slow.

步骤5如果S中还有未处理的列,执行步骤1.

步骤6结束.

输出：Sup和Slow.

类似地,如果对S逐行进行扫描,该算法可以同时检测出Sleft和Sright.

3 一种改进的膨胀和腐蚀优化算法

3.1膨胀和腐蚀的定义和时间复杂度本质上,膨胀和腐蚀是一种空域滤波,S对应滤波器.对于(x,y),滤波器的输出记为f(x,y),那么

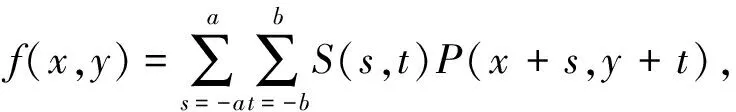
(6)

其中

0≤x≤v-1, 0≤y≤w-1,

a=(m-1)/2,b=(n-1)/2,

S(x,y)和P(x,y)分别是S和P中的像素(x,y).如果P(x,y)按下列公式更新

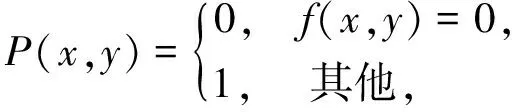
(7)

其中

0≤x≤v-1, 0≤y≤w-1,

那么,(6)和(7)式定义的操作就是膨胀.如果P(x,y)按下列公式更新

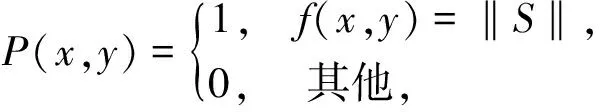
(8)

其中

0≤x≤v-1, 0≤y≤w-1,

‖S‖是S中1的个数.由(6)和(8)式定义的操作就是腐蚀.

从膨胀和腐蚀的定义可以看出,如果按照定义去计算膨胀和腐蚀操作(标准算法),算法的时间复杂度为O(v×w×m×n).

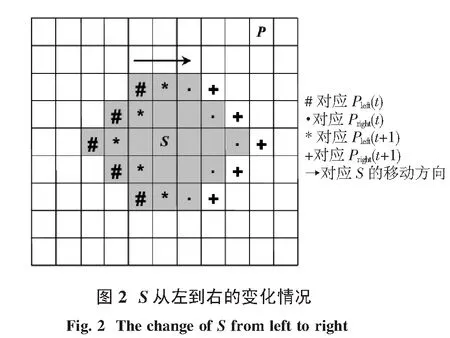
3.2一种改进的膨胀和腐蚀优化算法及时间复杂度如果P和S比较大的话,在(6)式中需要对P和S逐个像素地进行计算,因此膨胀和腐蚀是非常耗时的操作.同时,通过前面的分析可以看出,(6)式中有些像素的计算是没有必要的.如图2所示,如果S从左向右水平方向移动,t时刻和t+1时刻滤波器的输出分别为f(x,y)和f(x+1,y).假设Pleft(t)是t时刻P中和Sleft重叠的像素.类似地,可以定义Pright(t)、Pup(t)、Plow(t).从图2可以得到

f(x+1,y)=f(x,y)+

‖Pright(t+1)‖-‖Pleft(t)‖.

(9)

相反,如果S从右向左水平方向移动,t时刻和t+1时刻滤波器的输出分别为f(x,y)和f(x-1,y).类似地可以得到

f(x-1,y)=f(x,y)+

‖Pleft(t+1)‖-‖Pright(t)‖.

(10)

最后,如果S从上自下垂直方向移动,t时刻和t+1时刻滤波器的输出分别为f(x,y)和f(x,y+1),那么可以得

f(x,y+1)=f(x,y)+

‖Plow(t+1)‖-‖Pup(t)‖.

(11)

图2中S从左向右水平方向移动,Pleft、Pleft(t+1)、Pright和Pright(t+1)的变化情况.阴影区域表示t时刻和S重叠的P(x,y).显然,在t时刻,Pleft、Pleft(t+1)和Pright(t)位于阴影区域；在t+1时刻,Pleft(t+1)、Pright(t)和Pright(t+1)位于阴影区域.也就是说,从t时刻到t+1时刻,Pleft移出了阴影区域而Pright(t+1)移进了阴影区域.

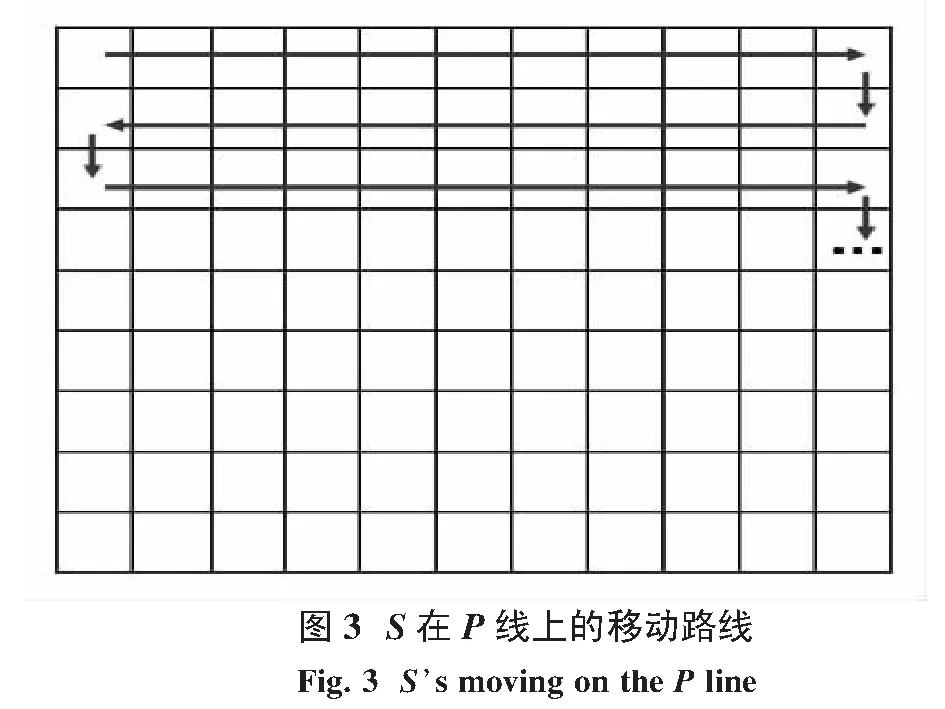
(9)～(11)式意味着如果S连续地在P上逐个像素的移动,膨胀和腐蚀可以被定义为迭代操作.进一步,如果S在P上的移动路径如图3所示,根据S的移动方向,(9)～(11)式中始终有且仅有一个等式适合当前的迭代计算,除f(0,0)的计算例外.事实上,f(0,0)的初始化计算可以按照(6)式进行.显然,因为只有一个像素需要这样计算,所以f(0,0)的初始化并不会提高膨胀和腐蚀优化算法的时间复杂度.

膨胀和腐蚀的优化算法完整地描述如下：

输入：S和P.

步骤1调用边界检测算法,检测得到Sup、Slow、Sleft和Sright.

步骤2根据(6)式计算f(0,0).

步骤3如果P(x,y)处理完成,跳转到步骤9.

步骤4如果S从左向右水平方向移动,根据(9)式计算f(x,y).

步骤5如果S从右向左水平方向移动,根据(10)式计算f(x,y).

步骤6如果S从上向下垂直方向移动,根据(11)式计算f(x,y).

步骤7根据(7)或(8)式更新P(x,y).

步骤8跳转到步骤3.

步骤9结束.

输出：P.

在上述优化算法中,步骤3对应一个二重循环,时间复杂度为O(v×w)；因为步骤4～6中可以直接调用边界检测算法的结果,所以时间复杂度为O(m)或O(n).整体而言,膨胀和腐蚀优化算法对应一个三重循环,时间复杂度不会超过O(n3),n=max{v,w,m,n}.

4 实验和结果

在实验中,P和S采用随机方式初始化为二值矩阵.同时,为了简化实验参数的设置,不失一般性,重新定义P∈Rv×w和S∈Rm×n.通过记录算法在不同参数条件下运行所需要的时钟脉冲数,优化算法和标准算法、Yang算法[14]进行对比.在实验中,采用的硬件平台为：CPU为酷睿i3,主频2.4 GHz,16 G DDR2 RAM,工作频率1 200 MHz.算法采用Visual Studio 2008编码实现.3种算法都采用C语言实现,同时,在C语言中,1 s包含了1 000个脉冲,因此实验结果精度为0.001 s.

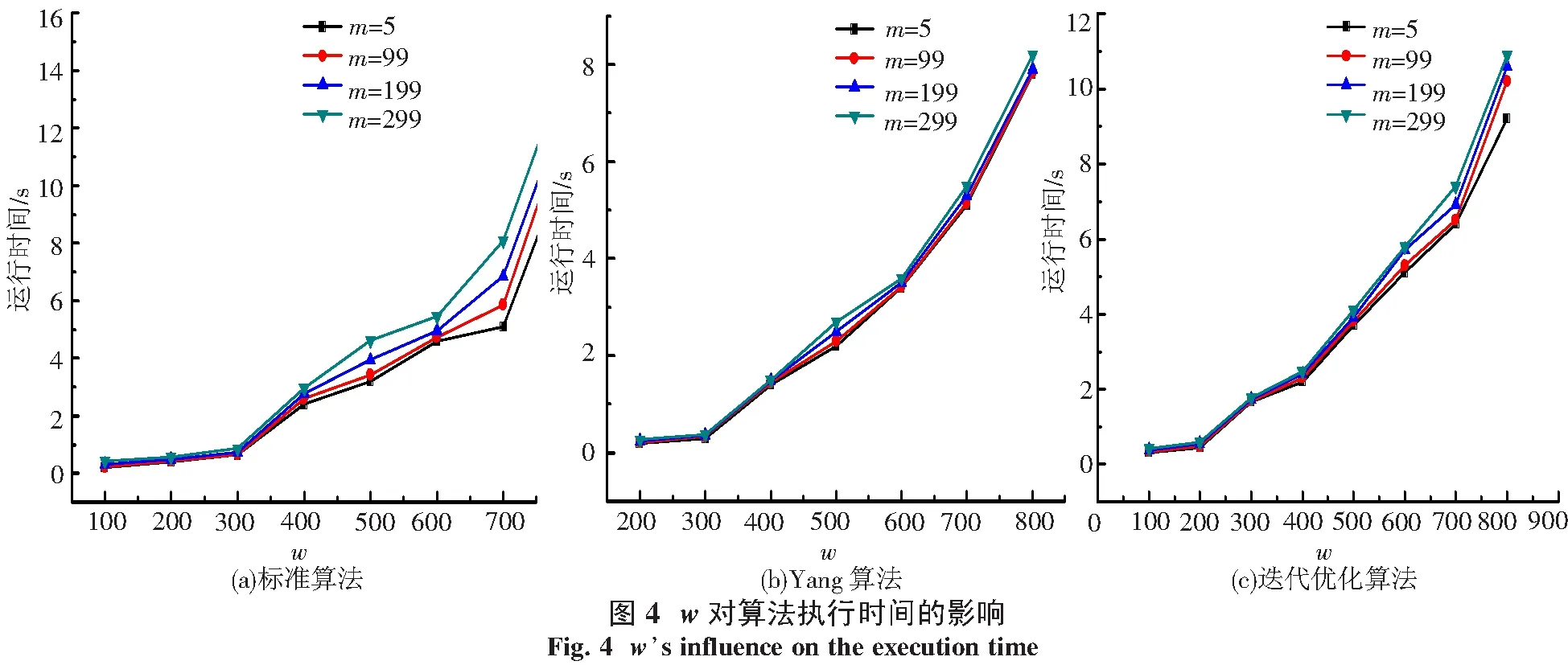
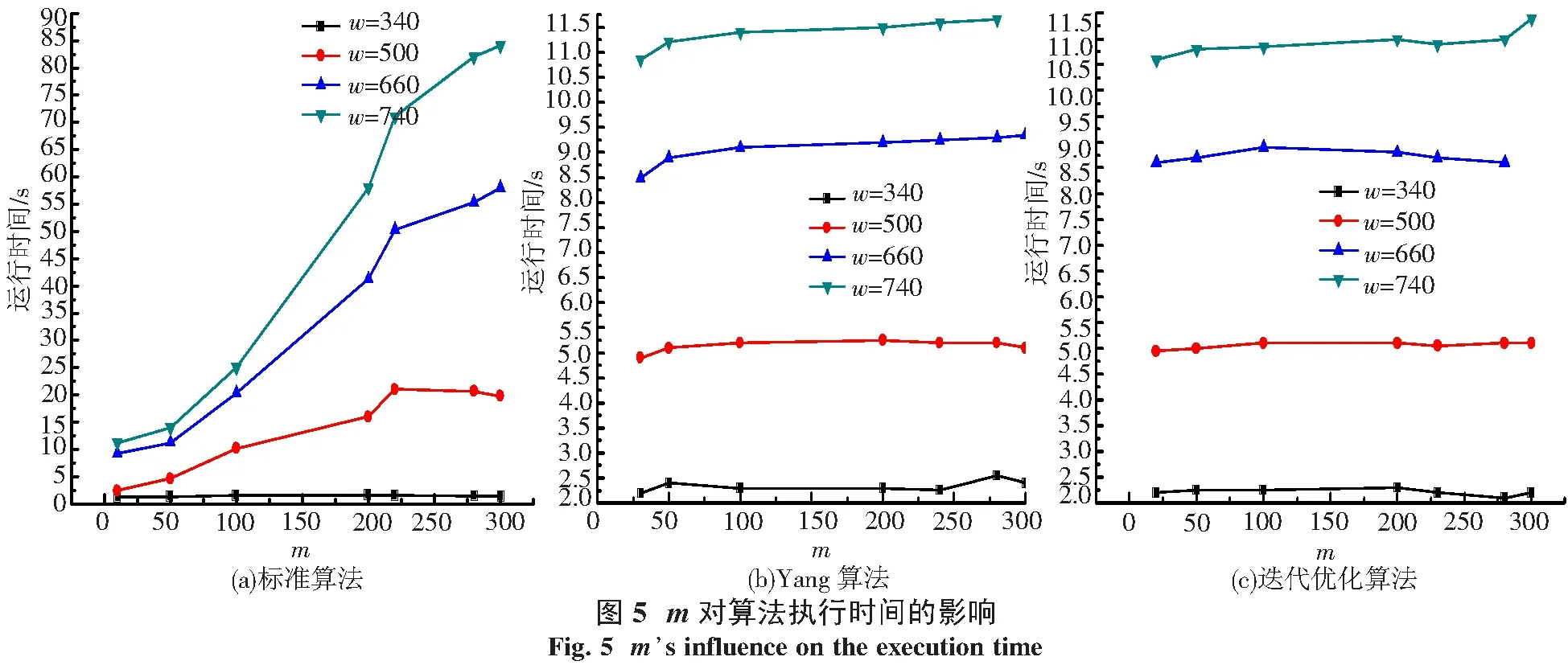
3种算法的对比结果如图4和图5所示.图4显示w对算法执行时间的影响.根据(6)式,对标准的膨胀和腐蚀算法而言,算法执行时间和w应该是二次函数关系,图4(a)证实了这一结论.类似地,根据图4(b)和图4(c),这一结论同样适合Yang算法和迭代优化算法.此外,从图4中还可以看出,当m取不同值时,优化算法的曲线最靠近,标准算法的曲线最分散,Yang算法的结果介于两者之间.这种现象说明在优化算法中,参数m对算法执行时间的影响最小.

5 小结

本文对数学形态学中的膨胀和腐蚀操作进行了研究.膨胀和腐蚀是数学形态学中最基础的2个操作,如果按照膨胀和腐蚀的定义去操作,算法的时间复杂度为O(n4).在本文中,通过定义结构元素的边界和内部点,膨胀和腐蚀操作被定义为一系列迭代计算.在此基础上,提出一种膨胀和腐蚀的迭代优化算法.该算法能利用上一次计算的结果,仅需要对边界进行重新计算.算法分析和实验结果都表明,迭代优化算法的时间复杂度为O(n3).实验结果同时还表明,当w≥300时,迭代优化算法的性能优于Yang算法的性能.

[1] Pitas I, Venetsanpoulos A N. Morphological shape decomposition[J]. IEEE Trans Pattern Anal Machine Intell,1990,12(1):38-45.

[2] Haralick R M, Stemberg S R, Zhuang X. Image analysis using mathematical morphology[J]. IEEE Trans Pattern Anal Machine Intell,1987,9(4):532-550.

[3] Zhuang X, Haralick R M. Morphological structuring element decomposition[J]. Comput Vision,Graphics,Image Processing,1986,35(9):370-382.

[4] Xu X. Decomposition of convex polygonal morphological structuring elements into neighborhood subsets[J]. IEEE Trans Pattern Anal Machine Intell,1991,13(2):153-162.

[5] Park H, Chin R T. Optimal decomposition of convex morphological structuring elements for 4-connected parallel array processors[J]. IEEE Trans Pattern Anal Machine Intell,1994,16(3):304-313.

[6] Hashimoto R F, Barrera J, Ferreira C E. A combinatorial optimization technique for the sequential decomposition of erosions and dilations[J]. J Math Imaging Vision,2000,13(1):17-33.

[7] Zhuang X. Decomposition of morphological structuring elements[J]. J Math Imaging Vision,1994,4(1):5-18.

[8] Pardalos P M, Sussner P, Ritter G X. On integer programming approaches for morphological template decomposition problems in computer vision[J]. J Combinatorial Optimization,1997,1(2):165-178.

[9] Park H, Chin R T. Decomposition of arbitrarily shaped morphological structuring elements[J]. IEEE Trans Pattern Anal Machine Intell,1995,17(1):2-15.

[10] 杨琨,曾立波,王殿成. 数学形态学腐蚀膨胀运算的快速算法[J]. 计算机工程与应用,2005,41(34):54-56.

[11] Anelli G, Broggi A, Destri G. Decomposition of arbitrarily shaped binary morphological structruing elements using genetic algorithm[J]. IEEE Trans Pattern Anal Machine Intell,1998,20(2):217-224.

[12] Hashimoto R F, Barrera J. A note on Park and Chin’s algorithm[J]. IEEE Trans Pattern Anal Machine Intell,2002,24(1):139-144.

[13] 景小平,邓方源,易世君,等. 基于形态小波变换的指纹图像识别预处理的应用研究[J]. 四川师范大学学报:自然科学版,2009,32(5):694-697.

[14] 林江莉,汪天富,彭玉兰,等. 乳腺肿瘤超声图像形态特征选择[J]. 四川师范大学学报:自然科学版,2005,28(5):615-618.

[15] 王贤秋,李咏红,陈顺玲. 基于形状和结构特征的白酒识别方法研究[J]. 四川师范大学学报:自然科学版,2011,34(4):593-596.

[16] 王大海,靳冰,贾玉珍. 基于双结构元素的数学形态学边缘检测方法[J]. 西华大学学报:自然科学版,2010,29(5):42-44.

[17] 高国明,黄汉明,李莉. 一种分形和形态学结合的图像边缘检测算法[J]. 广西师范大学大学学报:自然科学版,2012,30(3):50-54.