基于双线偏振多普勒雷达识别地物回波

曹 杨，苏德斌，周筠王君，徐文静

(1.成都信息工程学院大气科学学院，四川成都610225;2.北京市气象局，北京100089)

0 引言

随着电子及计算机技术的发展，多普勒天气雷达已成为降水、风及雷暴等大气现象不可或缺的重要手段，被广泛应用于天气监测和气象科学研究[1－2]。雷达在探测降水目标的同时，也受到非降水目标的影响，产生非降水回波信号，严重影响其业务应用，特别是在定量降水估测、数值模式预报、临近预报等雷达数据的定量应用中。非降水回波主要分为3类:大气中的昆虫、鸟、蝙蝠、谷壳等产生的生物回波;来自像建筑物、山峰、树木等固定目标的地物杂波(Normally-Propagated ground clutter);由于被观测区域大气温度和湿度发生变化，雷达波束折向地面引起的异常传播的地物杂波，称为超折射回波(Anomalous Propagation ground clutter)[3]。

为此，国内外学者进行广泛的研究，如Steiner，ea ta[3]及Zhang[4]建立决策树方法识别超折射回波。Kessinger[5]在Steiner等的研究基础上，设计一种基于模糊逻辑算法的雷达回波分类方法，区别降水回波和非降水回波。随后，Berenguer等[6]及 Cho and Lee[7]对 Kessinger的算法进行改进。刘黎平[8]基于 Kessinger 2003年提出的模糊逻辑算法，提出分步识别超折射地物回波，该算法能有效识别超折射地物回波，减少了地物回波的漏判和降水回波的误判。随后，江源[9]，庄薇等[10]对刘黎平的算法进行改进。但是当超折射回波与降水回波混合时，常规多普勒天气雷达识别效果始终较差。

近年，双线偏振雷达已成为天气雷达发展的重要方向，新一代双线偏振多普勒天气雷达不仅能提供回波强度、径向速度和速度谱宽等常规参量，同时还能提供多种偏振参量，提供更多的杂波特征，这些偏振参量的应用为非降水回波的识别及去除提供了有效的技术手段[11]。早在20世纪90年代，Ryzhkov等[12]就发现非降水回波的双线偏振参数ZDR和ΦDP的空间变率比降水回波大，而交叉相关系数(ρHV)通常比降水回波低。Gourley et al[13]，及Hubbert等[14]根据各类回波特征加入偏振参量，对模糊逻辑算法进行改进。准确有效的定量降水估测依赖于好的雷达数据质量[15－16]，因此发展利用偏振参量识别和滤除非降水回波，有效提高雷达数据质量非常必要，国内对这方面的研究较少。

由于使用地物杂波滤波器对北京市气象局C波段双线偏振多普勒天气雷达数据有很大的负面影响，因此该雷达所有数据均为使用地物杂波滤波器，因此研究雷达数据地物杂波后处理方法是非常有必要的。在此基础之上，分析了北京市气象局C波段双线偏振多普勒天气雷达的降水回波和地物回波特征，在刘黎平的模糊逻辑算法基础上选择容易区分降水回波和地物回波的特征量，加入偏振参数构成偏振模糊逻辑算法，与刘黎平的常规模糊逻辑算法进行对比，并选择个例对识别效果进行分析。

1 雷达概况

北京市气象局C波段双线偏振多普勒天气雷达是SCRXD-02MP型雷达系统，采用“双发双收”体制，是中国自行研制的首部C波段固定式“双发双收”体制双线偏振天气雷达，位于东经116°17'25″和北纬39°56'42″。该雷达与单偏振多普勒天气雷达相比，还提供差分反射率因子ZDR、差分传播相位ΦDP、差分传播相移率KDP、零滞后相关系数ρHV和线性退偏振比LDP等观测信息，其中KDP参数数据质量较非常差，不可用。雷达系统的主要性能指标如表1所示。

表1 雷达系统主要性能指标

该雷达于2011年12月完成“双发双收”体制双偏振功能改造，2011年12月1日雷达开始持续拷机观测，12月2日北京出现初雪天气，获取降雪观测资料。2012年开始对设备进行调试，4～9月C波段雷达开展了汛期强对流天气观测并保存个例数据，并采用“721特大暴雨”的个例数据对双偏振参数进行初步分析，至11月底基本完成设备的调试工作。随后开展降水粒子相态识别的研究，并取得一定的成果。

2 回波特征分析及识别方法

2.1 回波特征分析

图1 雷达参数PPI平面图(0.5°仰角)

研究发现，地物回波除了具有径向速度接近零、反射率空间变率或梯度较大、回波顶高较低等特征，地物回波的差分反射率和差分传播相移的波动性较大，差分反射率和差分传播相移的纹理特征值也较大，而零相关系数一般低于0.8。应用偏振参数识别地物回波比只利用常规参数识别效果更好，不仅能识别与降水回波分离的地物回波，对混合时的识别效果也较好，而且不会造成较远处小雨的丢失。

图1为北京市气象局C波段双线偏振多普勒天气雷达2012年7月21日15时01分(北京时间)(下同)观测到的0.5°仰角的PPI(Plan Position Indicating)图。雷达位于圆心，最大观测距离为150km，距离圈间隔30km，射线间隔为30°。黑色圆圈部分即为超折射地物回波，从图中可以看到，超折射地物回波的反射率值大于50dBz，比周围回波明显偏大很多;径向速度在零附近，速度谱宽较小，接近于零;差分反射率因子明显偏大或偏小，成正负间隔，变化较大;差分传播相移的波动幅度也较大，完全不同于降水回波，与许多学者的研究结果比较一致。虽然大部分地物回波的零滞后相关系数都小于0.9(一般认为降水回波大于0.9)，但仍然有部分大于0.9，与降水回波的区分不明显，并且一些降水回波区域反而小于0.9，因此文中ρHV不参与识别。

2.2 回波识别方法

针对北京市气象局C波段双线偏振多普勒雷达观测数据特征，采用模糊逻辑算法识别地物杂波。在计算各参数之前，首先对数据资料进行简单预处理:

(1)径向排序:雷达在固定仰角沿径向进行360度扫描取样，每一个PPI平面的径向个数不同，每一个平面的起始方位角也不固定，因此对最低3层仰角数据进行处理。由于该雷达分辨率较高，按0.6度为一个间隔进行排序，满足每个PPI平面都是600个径向。

(2)滤除孤立点回波:在PPI平面上，移动一个5×5(25个点)的窗口，如果该窗口中心点周围的有效点个数与总个数的比值少于某一阈值(一般取为55%)时，认为该中心点为无效值，作为孤立回波去除。公式如下:

其中Zi，j为(i，j)距离库上的反射率因子，spval为无效观测值，NZ为有效观测点个数，Pi，j为窗口中有效点个数与总个数的百分比。

图2 基于模糊逻辑的地物回波识别算法流程图

选用北京市气象局C波段双线偏振多普勒雷达2012年4月19日观测到的晴好天气低仰角(第1～2个仰角)数据和2012年7月21日到22日降雨天气的高仰角(第5～7个仰角)数据作为地物回波和降水回波资料，统计刘黎平的7个特征参数以及偏振参数ZDR、ΦDP的水平纹理特征等9个物理量的分布概率。发现降水回波和地物回波的反射率垂直变化、沿径向方向的变号和径向速度的方差的概率分布相差不大，重叠区域较多，因此这些参量不作为新算法的输入参数。选择从回波强度中提取的反射率水平纹理TDBZ、径向的库间变化程度SPIN和径向速度区域平均值MDVE、速度谱宽的区域平均值MDSW，以及偏振参数ZDR、ΦDP的水平纹理特征等6个物理量作为偏振模糊逻辑算法的输入参数。图3为6个参量的概率分布图，对地物回波和降水回波的各参量的分布特征进行分析:

(1)由于地物回波形状多变，分布不均匀，其水平反射率纹理特征明显大于降水回波，且分布范围较大，从0到80均有分布，降水回波主要集中在0到20范围内;地物回波径向的距离库间变化程度也较大，主要分布在大于50%的区域，明显大于降水回波;

(2)地物一般是静止的，地物回波的径向速度和速度谱宽分布在零附近，降水回波的径向速度均匀分布在正负最大不模糊速度之间，速度谱宽一般较大;

(3)差分反射率和差分传播相移的分布特征比较一致，地物回波分布范围比较广，降水回波主要集中在零附近，分布特征明显不同。

图3 地物回波和降水回波各特征参数的概率分布图

因此使用这6个参数应该能有效区分降水回波和地物回波。基于模糊逻辑的地物回波识别算法流程图如图2所示。TDBZ、TZDR、TΦDP、SPIN的表达式如下:

其中，i，j是方位和距离的序号，NA、NR表示定义的方位和距离计算范围，Zthresh为距离库间强度变化的阈值，一般取2～5dBz，文中取3dBz。

根据这些输入参数的概率分布，给出了各个参数的隶属函数(图4)，其中常规参量的隶属函数采用梯形折线表示，偏振参量采用不对称梯形函数表示。采用等权重求和法得到隶属函数值，即各输入参数的权重均采用1，与给定的阈值(0.5)比较，大于该阈值就认为是地物回波。通过检查本层径向速度和上一层放射率强度值，对识别为地物回波的距离库进一步确认，误判为地物的距离库采用处理前的上层反射率值代替，减少了对降水回波的误判。确定为地物回波的距离库标记为无效值去除，仅保留降水信息用于进一步应用。

3 识别效果分析

图4 地物回波识别各特征参数的隶属函数

2012年7月21日10时至7月22日06时，北京市出现历史罕见强降雨过程，大部分地区出现了大暴雨到特大暴雨天气过程。这次强降雨过程雨量大、强降水持续时间长、影响范围广、社会关注度高。对该雷达2012年7月22日02时57分在北京地区观测的地物回波识别效果进行分析，图5给出第二层(1.5°仰角)PPI的原始回波强度图(5a)，采用刘黎平的常规模糊逻辑算法识别地物回波的回波强度图(5b)，以及利用加入偏振参量的偏振模糊逻辑算法识别后的回波强度图(5c)。图5(a)中椭圆部分即为地物杂波，从图5(b)、(c)可以看到，常规模糊逻辑算法和加入偏振参量的模糊逻辑算法均能有效识别大部分地物回波，特别是西北方向和西方回波强度比较大的地物回波，地物回波识别面积基本相同。但是，采用常规模糊逻辑识别方法，有一小部分径向速度不为零的地物回波(图5b灰色方框部分)未能识别，而零速度降水区(图5b空方框部分)又被误判为地物回波。2种算法均不能很好识别雷达周围强度较弱的地物回波。采用加入偏振参量的模糊逻辑识别算法，零速度降水区被误判为地物回波的情况明显改善。

分析该区域各参数径向的距离廓线图发现，出现这种误判的原因主要是降水回波的移动速度较慢，径向速度接近于零，速度谱宽也较小(图6a、6b)，常规的模糊逻辑算法主要依靠强度因子和速度相关参数进行判断，很容易将这部分降水回波误判为地物回波。分析零速度降水区径向的差分反射率因子和差分传播相移的距离廓线图(图6c、6d)，发现在常规识别算法中被误判为地物回波的“空洞”区域的差分反射率因子和差分传播相移波动较小，具有降水回波特性。加入偏振参量的模糊逻辑算法很好地解决了过度识别零速度降水区的问题，对地物回波识别效果有了较好的改善。从图5(c)可以看到，去除加入偏振参量的模糊逻辑算法识别出来的地物回波后，很好地保留了降水回波信息。

图5 2012年7月22日02时57分1.5°仰角(第二层)回波强度地物识别PPI

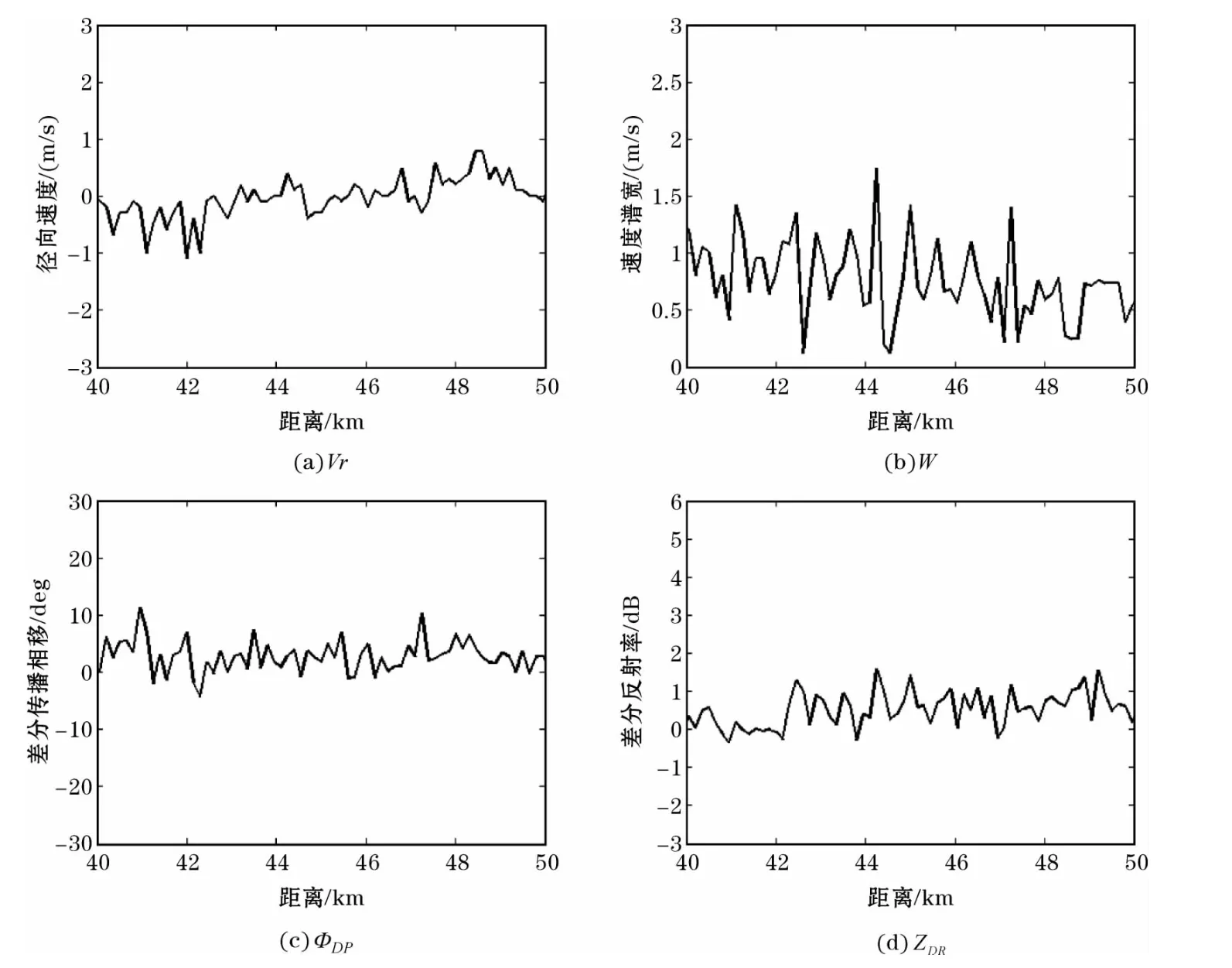
图6 图4(b)中72°方位角“空洞”区域各参数的距离廓线图

从图5可以看到，降水回波与地物回波分离时，偏振模糊逻辑方法的识别和去除效果较好。图7为一个降水回波与地物回波混合时的个例，为北京时间2012年7月21日15时12分1.5°仰角(第二层)回波强度PPI图。可以看到，当降水回波与地物回波混合时，两种方法均能很好识别和去除地物回波，但是采用常规模糊逻辑方法同样存在零速度区降水回波被误判无地物回波的问题，离雷达较远处这种现象更加明显(图7b方框部分)。

因此，加入偏振参量的模糊逻辑算法能有效识别并去除地物杂波，并较好地保留降水回波信息。

图7 2012年7月21日15时12分1.5°仰角(第二层)回波强度地物识别PPI

4 结论

采用北京市气象局C波段双线偏振多普勒天气雷达观测数据，对刘黎平识别地物回波的模糊逻辑算法进行改进，根据反射率因子、径向速度、速度谱宽、差分反射率和差分传播相移、零滞后相关系数等资料，对地物回波特征进行讨论，并根据其特征统计分析了识别地物回波的6个物理量，提出加入偏振参数的偏振模糊逻辑算法识别地物回波，并与刘黎平的常规模糊逻辑识别算法的识别效果进行比较，结果表明:

(1)降水回波和地物回波的TDBZ、SPIN、MDVE和MDSW4个参量的概率分布有明显区别，而GDBZ、SIGN和SDVE相差不大，因此只选前面4个参数作为新算法的输入参数。地物回波的ZDR和ΦDP的波动幅度较大，不同于降水回波，虽然大部分地物回波的零滞后相关系数小于0.9，但仍然有部分大于0.9，并且有些降水回波区域反而小于0.9，ρHV不参与识别。因此选择 TDBZ、SPIN、MDVE、MDSW、TZDR和 TΦDP6 个参数作为新算法的输入参数。

(2)该算法能有效识别地物回波，特别是强度较强的地物回波，并且很好地解决了过度识别零速度降水区的问题，对地物回波识别效果有了较好的改善。

(3)同时，发现偏振识别算法对雷达周围强度较弱的地物回波的识别效果与常规算法差别不大，均不能很好识别。对于结果的判定仍然采用人工判读的方法，评价结果没有定量化的检验，无法评价算法的好坏。而且，现在的质量控制方法只依靠雷达数据自身，应该进一步发展综合利用卫星、地面雨量站资料和雷达资料。

致谢:感谢北京市气象局气象科技研发专项资助项目(2013BMBKYZX04)对本文的资助

[1] Joss J，et al.The application of radar-gauge comparisons to operational precipitation profile corrections[J]，J.Appl.Meteor.，1995，34:2612－2630.

[2] Rosenfeld D.Classification of rain regimes by the three-dimensional proper ties of reflectivity fields[J].J.Appl.Meteor.，1995，34:198－211.

[3] Steiner M，Smith J.Use of three-dimensional reflectivity structure for automated detection and removal of nonprecipitating echoes in radar data[J].Atmos Ocea Tech，2002，5:673－686.

[4] Zhang J，Wang S，Clarke B.Wsr-88d reflectivity quality control using horizontal and vertical reflectivity structure[C].11thconference on aviation，range and aerospace meteorology.Hyannis，2004，54.

[5] Kessinger C，Ellis S，Van Andel J.The radar echo classifier:A fuzzy logic algorithm for the WSR-88D[C].3rdconference on artificial applications to the environmental science.AMS Long Beach，CA，2003.

[6] Berenguer M，Torres S D，et al.A Fuzzy Logic Technique for Identifying Nonprecipitating Echoes in Radar Scans[C].JOURNAL OF ATMOSPHERIC AND OCEANIC TECHNOLOGY，2006，23:1157－1180.

[7] Cho Y H，Lee G W.Identification and Removal of Ground Echoes and Anomalous Propagation Using the Characteristics of Radar Echoes[C].JOURNAL OF ATMOSPHERIC AND OCEANIC TECHNOLOGY，2006，23:1206－1222.

[8] 刘黎平，吴林林，杨引明.基于模糊逻辑的分步式超折射地物回波识别方法的建立和效果分析[J].气象学报，2007，65(2):252－260.

[9] 江源，刘黎平，庄薇.多普勒天气雷达地物回波特征及其识别方法改进[J].应用气象学报，2009，20(2):203－213.

[10] 庄薇，刘黎平，余燕群，等.雷达地物回波模糊逻辑识别算法的改进及效果检验[J].气象学报，2012，70(3):576－584.

[11] 曹俊武，刘黎平，葛润生.模糊逻辑法在双线偏振雷达识别降水粒子相态中的研究[J].大气科学，2005，29(5):827－836.

[12] Ryzhkov A V，D S Zrnic.Polarimetric rainfall estimation in the presence of anomalous propagation[J].J.Atmos.Oceanic Technol.，1998，15:1320－1330.

[13] Gourley J J，Tabary P.A Fuzzy Logic Algorithm for the Separation of Precipitating from Non precipitating Echoes Using Polarimetric Radar Observations[R].2007.

[14] Hubbert J C，Dixon M，Ellis S M.Weather Radar Ground Clutter.Part II:Real-Time Identification and Filtering[R].2009.

[15] 毛紫阳，段崇雯，成礼智，等.模糊特征在天气雷达反射率基数据质量控制中的应用[J].模糊系统与数学，2006，20(6):136－142.

[16] 王建林.双线偏振多普勒雷达定量探测降水强度方法的研究[D].北京:中国气象科学研究院，2005:1－67.