基于拨销与轮槽创成及啮合仿真的槽轮机构设计*

陈殿华，蔡 军

(大连大学 机械工程学院，辽宁 大连 116022)

0 前言

普通的槽轮机构难免存在着柔性冲击，当用于高速传动时惯性载荷比较大，产生振动噪音，影响了机构的使用寿命、运动精度及强度稳定性。由于普通槽轮机构的参数对动载荷的影响［1］是确定的难以改变，为此人们提出了槽轮与凸轮、槽轮与连杆组合等各种组合机构。尽管机构组合的方法有效的改进了动力学特性，但随之带来一些弊端，如机构复杂，构件和运动副增多，不但增加制造成本也使机构的精度和效率受到影响。

为了减小惯性动载荷改善槽轮机构的动力学性能，本研究通过改变主动拨销和轮槽几何形状的方法来设计槽轮机构［2］。根据选定的运动规律，利用拨销与轮槽相对运动的创成原理进行拨销与轮槽的结构设计。由此原来的圆柱滾子拨销变成了非圆柱形的凸轮拨销，这样不但减少了构件和运动副数目，而且动力学参数对槽轮载荷大小和位置的影响是一种可调控的函数关系。通过优选运动规律，可实现槽轮无刚性和柔性冲击并减小动载荷［3］。所以本设计方法可有效地改善槽轮机构的动力学特性及使用效率和精度。

1 槽轮与拨销的运动学与动力学分析

为达到槽轮分度运动过程中无刚性、柔性冲击和减小动载荷，研究采用非圆截面式凸轮拨销。这样虽将原来的拨销与槽轮槽的滚动变成了滚动伴滑动，但减少了一个轴径滑动摩擦副。为说明凸轮拨销式槽轮机构的设计原理，首先从槽轮的运动分析开始，再根据运动学要求设计凸轮拨销，实现最佳的传动性能。

1.1 槽轮与拨销的运动学分析

由图1 可知槽轮是通过曲柄拨销与轮槽接触传动实现转位运动，对于普通槽轮机构，根据运动关系可写出槽轮与拨销曲柄转角(α 和θ)的相对运动方程:

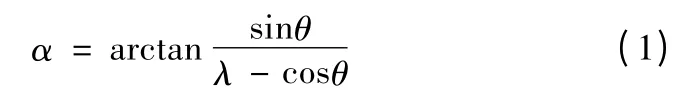
这里λ = R/L，是曲柄回转半径R = AB 与中心距L 之比，ωA为曲柄拨销的回转角速度。通过微分求导可得槽轮的角速度ω 和角加速度ε:

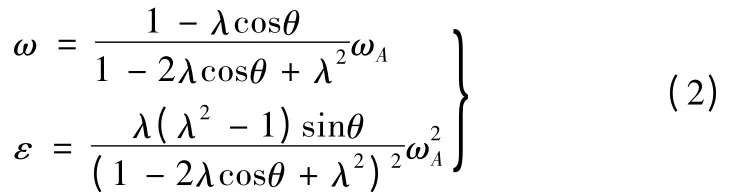
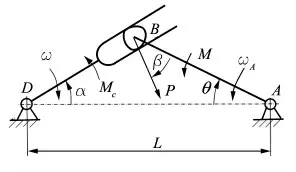
图1 凸轮销式槽轮机构的力学模型

依据普通槽轮机构的几何运动关系，可得槽轮速度和加速度最大值与槽轮槽数Z 的关系:

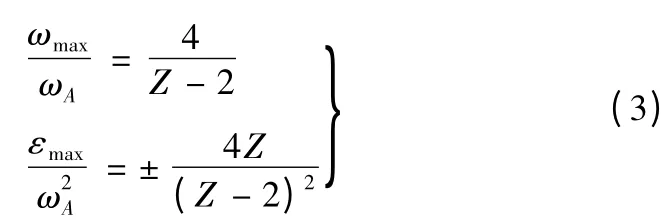
对于本设计的凸轮拨销式槽轮机构，其槽轮是按给定运动规律运动的。为了说明本设计的原理，现将槽轮回转的运动规律［4］选定为摆线运动规律，槽轮的角加速度给出如式(4):

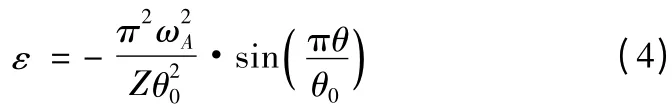
这里Z，θ0为槽轮槽数和拨销刚进入分度时曲柄与机架AD 的夹角，由式(4)通过积分并利用边界条件，可得槽轮的回转角速度与转角的表达式:

这与普通槽轮机构的运动规律是有所不同，由加速度函数式(4)可见，槽轮分度始末时的加速度为零，因此没有柔性冲击。

1.2 槽轮与拨销传动的动力学分析

槽轮机构的分度运动过程中，拨销与轮槽的接触载荷的大小和位置随时变化，而且针对不同的运动规律其变化差异很大。依据图1 所示的传动关系，可写出槽轮轴转动的动力学微分方程:

其中M 为驱动力矩，Mc 为阻力矩，Je为槽轮轴上的等效转动惯量，ε 为槽轮的角加速度。依照图1 所示的几何和运动关系及动力学分析，凸轮拨销对槽轮槽的接触动载荷P 可写为:

根据文献［4］的分析，最大惯性力矩可由下式求得:

其中tα为一次分度时间，α0为槽轮分度半角，(A×V)m为惯性力矩极值［4］。因为阻力矩在分度中是不变的，在分度的前半程中，当1/rd趋于最大(rd= L－R)时，凸轮拨销对槽轮槽的压力P 为最大，由式(8)可得:

由式(9)可知惯性力矩是角加速度和角速度的函数。由仿真分析得知，惯性载荷最大值与阻力载荷最大值发生位置不相同，最大压力将偏离两个载荷的峰值位置。对于不同运动规律式(10)中的偏置载荷系数kp= 0.85 ～0.93 之间选取。

研究以槽数Z = 4，摆线运动规律的凸轮拨销式槽轮为例，将槽轮运动的角加速度与普通槽轮的角加速度进行比较分析如图2。

图2 槽轮的角加速度变化曲线比较

普通槽轮机构的槽轮运动角加速度曲线不但在分度始末不为零、有突变，而且最大值较大。本设计的槽轮的角加速度在分度始末为零、没有突变，所以机构没有柔性冲击，而且最大加速度值比较小，仅为普通槽轮机构的74%，最大加速度值发生的位置是在分度行程中的2/8 和6/8 处，有效减小了接触动载荷P 的大小和位置，机构动特性得到改善。

2 拨销和轮槽的创成原理及仿真

实现槽轮的理想运动规律是通过优化设计凸轮销的廓线达到的，由图1 可知槽轮是由拨销与轮槽接触传动实现转位运动的，槽轮槽与凸轮销的相对运动关系是既有相对转动又有相对移动，是一种啮合传动。借鉴齿轮啮合的原理，根据选定的运动规律和拨销与轮槽的创成运动关系，可写出轮槽与拨销啮合的运动方程:

这里rd为轮槽接触中心的半径，即槽轮回转中心到轮槽的接触中心的距离，β 为接触点法线曲柄AB的夹角。根据凸轮廓线反转法设计原理，若将凸轮拨销固定不动，让槽轮槽(相当于刀具)一边绕凸轮拨销反向转动，一边沿轮槽方向相对移动，这样槽轮槽绕凸轮拨销中心运动轨迹包络出的曲线即是凸轮拨销的廓线。图3 为槽数Z =4 时，按照方程(4)的摆线运动规律，利用计算机图形创成仿真［5］方法完成的凸轮拨销的包络廓线。

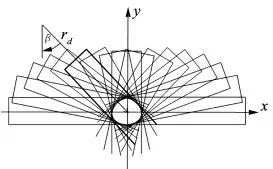
图3 销槽廓线形状的创成原理

需要注意的是，由于当曲柄与轮槽共线时(α =θ = 0)出现了rd= 0/0，因此需利用式(11)中α 与θ的函数关系和函数极限的罗彼塔法则求解［6］，上述位置的值可按下式来确定:

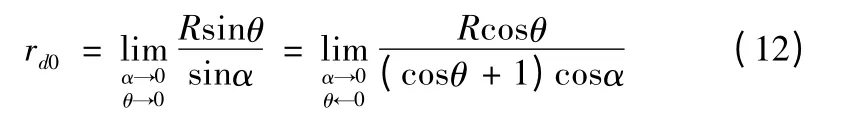
表1 接触中心的矢径rd(mm)与转角α 关系

表1 为槽数Z = 4，曲柄长R = 150mm 时按摆线规律运动时的拨销接触中心的轨迹(此为分度的前半程)。通过接触中心轨迹还可求得接触点的轨迹，进而得知凸轮拨销加工时刀具中心的路径。

由上述创成仿真分析可知，槽轮槽相当于刀具，所以轮槽的形状也会影响所创成的凸轮拨销的形状。通过改变轮槽的倾角和槽宽及槽形可得到不同形状的凸轮拨销廓线。如图4a 为轮槽的倾角3 度，槽宽为0.16L 条件下仿真出的凸轮销廓线，比轮槽的倾角为零度时的凸轮销廓线更加平缓滑顺，因凸轮销与轮槽接触传动过程中既有滚动又有滑动，所以良好的凸轮廓线有利于润滑的改善和强度的提高。图4b 将槽轮的槽形取为圆弧曲线，因廓线的曲率半径随负载增大而增大，所以接触和弯曲强度都得以提高。

图4 拨销与轮槽形状创成的仿真分析

凸轮销创成廓线仿真分析发现，采用不同的运动规律凸轮销廓线的形状差异较大而且槽轮槽倾角的选则对其影响也比较明显，因此在机构设计中应综合考虑，以得到最佳的运动特性和较高的强度和精度。

表2 给出了选择不同运动规律条件下对应的凸轮销廓线的仿真设计及其动力学特性。凸轮销廓线及运动特性仿真结果表明，通过凸轮拨销形状的设计实现优选运动规律，不但合理可行而且还为凸轮拨销的数控加工提供了数据。

表2 凸轮拨销与轮槽形状及动力特性设计例

从表2 可见变形正弦的动力学性能最好，研究进行了一系列的实例创成仿真分析，例如同一种运动规律，采用不同的轮槽倾角等，在此不再赘述。

3 槽轮分度传动的动载变化特征

在槽轮机构的分度运动过程中，拨销与轮槽的接触载荷的大小和位置随时变化，而且针对不同的运动规律其变化差异很大。由于惯性力矩是角加速度的函数，最大值发生位置不相同，最大接触动载荷将偏离惯性载荷与阻力载荷的峰值位置。

图5 是Z=4 时，槽轮按摆线规律运动的轮槽与凸轮销接触载荷在分度运动中的变化曲线，动载荷应为惯性载荷与阻力载荷的叠加。由图可见最大动载荷约发生在行程的3/8(正向)和5/8(反向)处，与惯性载荷峰值发生位置偏移。阻力引起的载荷最大值仍在行程的中间，所以最大接触载荷位置应在行程的3/8 ～4/8 之间。在行程后半惯性载荷与阻力载荷方向相反，对于高速大转动惯量的情况时阻力载荷小，最大接触载荷主要取决于惯性载荷，因此其位置接近最大角加速度发生的位置，而且是反向接触。

图5 轮槽接触动载荷在分度过程中的变化

4 结论

利用拨销与轮槽的创成运动分析设计主动件拨销和轮槽的形状，实现动件槽轮任意运动规律，不仅达到无刚性和柔性冲击，而且大大减小了动载荷，实现了槽轮动特性的改善，为高速分度机构设计提供了应用基础。通过对主动拨销形状设计及仿真分析，不但给出了拨销形状的优化设计方案，还可为拨销的数控加工提供加工数据。实例设计验证了不同运动规律、槽倾角、槽宽度和槽型对凸轮销形状的制约关系。轮槽接触最大压力分析表明，选用优良的运动规律可降低动载荷30 ～60%，显著改进高了槽轮机构的动力学性能。

［1］陈殿华，田中道彦. ゼネバ機構動特性に関する基礎的研究［J］. (日本)設計工学，1997，32(9):369－374.

［2］K.S.H. Sadek，J.L.Lloyd. A New Design of Geneva Drive to Reduce shock loading［J］，Me. Mach. Theory，1990，25(6):589－595.

［3］成刚虎，张磊. 一种新型槽轮机构的设计与应用研究［J］. 机械科学与技术，2007，26(11):129－133.

［4］牧野洋. 自动机械机构学［M］. 北京:科学出版社，1980.

［5］王良文，杜文，等. 自动机械中槽轮机构参数化设计与仿真［J］. 机械设计，2006，129(12):35－38.

［6］陈殿华. 槽轮机构的计算机辅助设计［J］. 机械设计与制造，1992，36(2):17－19.