光纤陀螺跟踪角加速度模型建模与研究
苏晓东 宋蔚阳 吴昭辉 肖凯 牟炳富


摘要 本文建立了全数字闭环光纤陀螺动态模型,通过对该模型施加线性增长(或减小)的输入角速率激励,对光纤陀螺的角加速度跟踪能力进行了仿真,并且分析了光纤陀螺跨条纹工作的机理和跨条纹工作的条件。通过试验验证,提出了提高光纤陀螺在高频冲击下适应性的可行方法。
【关键词】光纤陀螺 大动态 动态模型 角加速度
光纤陀螺是一种新型全固态陀螺,具有无运动部件和磨损部件,成本低,寿命长,重量轻,体积小,动态范围大,启动时间短、精度应用覆盖面广,抗电磁干扰,无加速度引起的漂移,结构设计灵活,生产工艺简单等优点。
在系统应用中,光纤陀螺的性能是一个非常重要的指标,文献[4]通过研究电源噪声来提高光纤陀螺精度指标。文献[5]及文献[6]通过对温度补偿方法的研究,来提高系统导航精度。除此以外,光纤陀螺的静态性能及动态性能也必须满足系统的要求,特别是应用于高动态环境下的系统,对动态性能的要求非常严格,否则,由于陀螺整体动态性能不足或陀螺相互之间的动态性能相差过大,都有可能会增大系统的解算误差。
本文建立光纤陀螺的动态模型后,可以通过施加线性增长(或减小)的输入角速率激励,对光纤陀螺的跟踪角加速度进行仿真,并分析了光纤陀螺跨条纹工作的机理,讨论了光纤陀螺跨条纹工作这种异常现象产生的条件。通过实物产品的验证试验,提出了提高光纤陀螺在高频冲击下适应性的可行方法。
1 光纤陀螺的传递函数
图1为全数字闭环光纤陀螺的原理框图。
由图1可知,光纤陀螺中的光学部分可简化为一个比例环节,陀螺的角速度可通过角加速度的一次积分累加得到。
不妨设反馈通道的增益为K2,从光纤环到数字解调的增益为K1,则在偏置工作点设置为PI/2时,光强曲线为位相为自变量的余弦曲线(给定振幅为1),可以推导出第n个周期工作点的光强分别为:
其中,I1及I2分别为在第n个周期,输入位相差(对于光纤陀螺等同于输入角速率)为IP(n)时,PI/2及-PI/2工作点的实际光强,此时的反馈为上一个周期的反馈量大小,为feedback(n-1)。
第n周期的陀螺输出为:
第n周期的反馈量为:
给出不同的增益大小K1及K2,同时给出不同的输入角速率IP(n),即可对输出进行动态仿真。
2 跟踪角加速度仿真结果
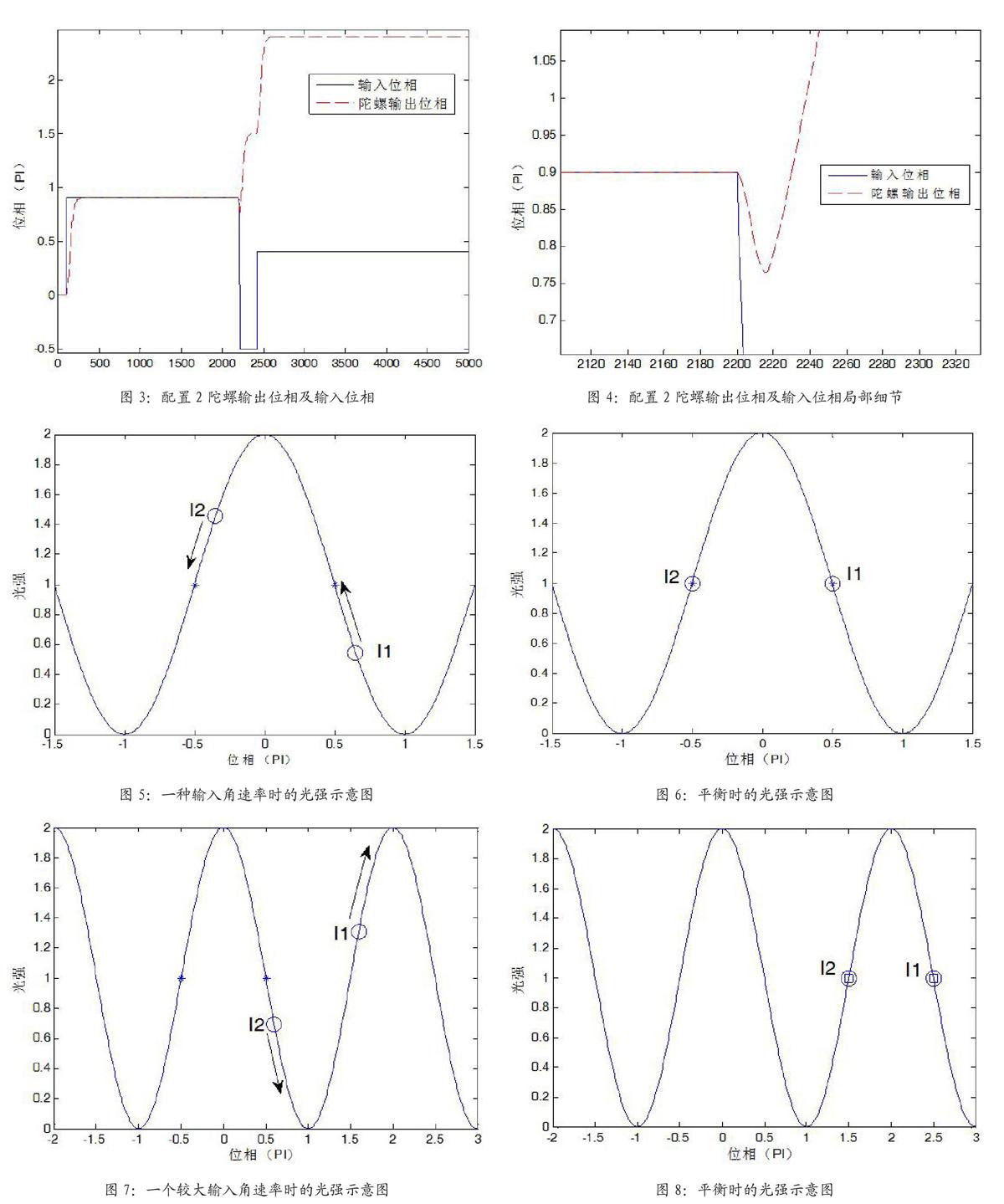
图2给出了一种参数配置情况下陀螺输出随输入位相变化的仿真结果,输入位相从0变化到0.9PI,然后变化到-0.48PI,陀螺的输出可以跟踪输入位相,不存在输入输出反向等不正常现象。图3给出了另一种参数配置情况下陀螺输出随输入位相变化的仿真结果,保持同样的输入位相,陀螺输出在输入位相从0.9PI变化到-0.48PI时出现了输入输出反向的情况,图4给出了这种情况发生时的局部细节,开始时,输出随输入减小,随后输出出现了变化趋势反向的现象,陀螺不再能正常跟踪输入角速率,陀螺输出稳定后也会同样输出不正常的角速率,出现了跨条纹工作的现象。
3 跨条纹工作机理分析
图5给出了一种输入角速率时光强的变化情况示意图,该图中横轴为位相,也可对应角速率输入,纵轴为光纤陀螺的干涉光强。陀螺工作点为±PI/2,在图中分别用*号进行了表示。当出现一个正的位相(及角速率)时,由于反馈的作用,I1I2分别沿着箭头指出的方向变化,最终平衡于图6所示的状态。
图7给出了陀螺接收到瞬间一个较大输入角速率(即角加速度也较大)时光强的变化情况示意图,此时两个工作点光强分别为I1I2,由于I1-I2的符号与图5所示的情况相反,会使得反馈位相增加,从而使得出现图7中光强箭头的运行方向,也就是出现了正反馈,最终平衡于图8所示的情况,此时的平衡点用方块进行了表示,分别为1.5PI和2.5PI,不再是±PI/2,出现了跨条纹工作的现象。
从图5~8可以看出,只有在瞬间位相差超过PI时,才会出现跨条纹工作的现象,因为整个过程中出现了正反馈,将不能输出正确的角速率量,和图3给出的现象类似。显然一个较慢的角加速度输入时,动态模型将始终能够将I1I2“拉回”图6所示的工作点;当角加速度足够大(也就是角速率变化足够快),且同时角速度变化量足够大(超过PI)时,会出现光纤陀螺跨条纹工作的情况。
4 原理验证及对比
选择某台具有四个安装支耳的惯性组合1号在如表1条件下进行高频冲击试验。惯性组合在X方向的高频冲击结果如图9所示。可见,YZ轴最大角速率均为70o/s左右。
选取另一台具有三个安装支耳的非对称结构惯性组合2号在如下条件下进行高频冲击试验,惯性组合在X方向的高频冲击结果如图10所示。可见,第二次冲击后,Y轴已限幅,YZ轴在冲击中达到了350o/s(有可能更大,因为IMU内部将输出限幅在了350o/s),这已高于理论值330o/s,此时如果角加速度足够大就会导致输出紊乱,第一次冲击正常,第二次冲击后Y轴限幅输出证明了这种试验条件已经处于临界状态。如表2所示。
冲击条件降为1000g后的试验情况如图11所示。
图11中YZ轴最大角速率均低于170o/s,相对于330o/s的限制有较大余量。
由于1号惯组在1500g高频冲击下的最大角速率为70o/s,2号惯组在1000g高频冲击下的最大角速率为170o/s,也就是1号惯组在更大的冲击下最大角速率反而更小。
由于减振器的存在,产品在冲击情况下必然存在晃动,其角速率必然是放大的。1号惯组与2号惯组在结构方面的主要区别是1号為4点减振,2号为3点减振,两个产品的减振器刚度选取完全一致,可以得出在等量级冲击下,4点减振比3点减振更加稳定,晃动更小,角速度变化更小的结论。
5 结束语
建立全数字闭环光纤陀螺动态模型,对该光纤陀螺模型施加线性增长(或减小)的输入角速率激励,对光纤陀螺的角加速度跟踪能力进行了仿真,当施加一个较慢的角加速度输入时,动态模型将始终能够将I1I2“拉回”原平衡工作点,但当同时满足角加速度足够大(也就是角速率变化足够快);角速度变化量足够大(超过PI)时,会出现光纤陀螺跨条纹工作的情况,此时陀螺工作于非正常状态,不能输出正确的角速率量。
通过试验验证,要使产品在高频冲击下能正常工作有以下技术途径供参考:
(1)采用更加稳定的4点减振支撑结构;
(2)选用刚度更高的减振器(需与振动等环境适应性综合考虑);
(3)提高光纤陀螺在高频冲击下的适应性可以从以下2方面考虑:降低光纤环长度或总面积(需同时考虑对陀螺性能的影响);提高陀螺的闭环带宽或增益(需同时考虑能否满足用户对产品带宽的要求)。
参考文献
[1] 张桂才编著.光纤陀螺原理与技术[M].北京:国防工业出版社,2008.
[2] 王磊,陈杏藩,刘承,舒晓武.大动态光纤陀螺及其应用[J].现代防御技术,2017,45(06):1-4.
[3] 肖凯,叶刚,贾晓明.光纤陀螺传递函数的数字信号辨识法[J].压电与声光,2011,33(04):547-548+553.
[4] 陈贤,杨建华,周一览,舒晓武.一种低噪声开关电源在光纤陀螺系统中的应用[J].光电工程,2018,45(01):34-42.
[5] 汪红兵,王新宇,阳洪.基于光纤陀螺温度漂移误差补偿方法研究[J].压电与声光,2018,40(02):199-201.
[6]赵龙,胡少波,纪文涛.光纤惯组温度补偿模型和测试技术研究[J].导弹与航天运载技术,2016(04):39-43+55.
[7]严恭敏,严卫生,徐德民等,抖动偏频激光陀螺整周期采样对捷联惯导姿态解算的影响[J].传感器技术学报,2007,20(10):2268-2271.

