制造误差影响齿轮副啮合的接触有限元分析方法

第一作者张涛男，博士生，1988年生

通信作者王建军男，博士，教授，1956年生

制造误差影响齿轮副啮合的接触有限元分析方法

张涛1，吴勇军2, 吴静3，王建军1

(1.北京航空航天大学能源与动力工程学院，北京100191;2. 中国运载火箭技术研究院研究发展中心，北京100076;3. 北京动力机械研究所，北京100074)

摘要：制造误差是影响齿轮副啮合的重要因素，研究其作用机理对齿轮的减振设计具有重要意义。首先基于几种典型制造误差的结构形式提出了一般的精确建模方法，以一对渐开线直齿轮为例，利用接触有限元分析方法对啮合过程进行仿真，发现理想齿轮副和含误差齿轮副啮合过程中的角速度、动态接触力特性表现出显著差异。然后进行单项误差影响齿轮振动的机理研究，分别以齿廓误差和齿距误差为对象，利用傅里叶变换量化分析了不同加工公差等级下的单项制造误差对齿轮副动态传递误差、角加速度特性的影响规律。研究表明：所提出的建模方法可以模拟任意形式的微小量级的制造误差，并体现在接触有限元分析中。不但能够用于精细化研究制造误差对齿轮副啮合过程的影响，还可以通过量化各项啮合特性分析单项误差影响齿轮振动的作用机理，并指导齿轮的减振设计和精度设计等。

关键词：制造误差；齿轮副；动态啮合特性；接触有限元分析；动态传递误差；角加速度

收稿日期：2013-10-21修改稿收到日期：2013-12-24

中图分类号:TH132文献标志码：A

基金项目：国家自然科学

Analysis of machining errors’ effects on gear pair meshing using contact finite element method

ZHANGTao1,WUYong-jun2,WUJing3,WANGJian-jun1(1. School of Jet propulsion, Beijing Univ., of Aeronautics & Astronautics, Beijing 100191, China;2. China Academy of Launch Vehicle Technology, Beijing 100076, China;3. Beijing Power Machinery Institute, Beijing 100074, China)

Abstract:Machining errors have significant effect on gear pair meshing, it is necessary to study its mechanism for vibration reduction design of gear pairs. Based on the analysis of several kinds of machining errors, a precise modeling method was presented. On this basis, the meshing process of one spur gear pair as an example was simulated using the contact finite element method. Its angular velocity and dynamic meshing force showed significant differences between an ideal gear pair and a gear pair with machining errors. Then, the influence mechanisms of profile error and pitch error on gear vibration were studied, respectively. Quantitative analysis of meshing characteristics including dynamic transmission error and angular acceleration was performed using FFT. The results showed that the proposed modeling method can be used to simulate arbitrary form of machining errors with a small order and this ability is reflected in the contact finite element analysis; it is effective not only to investigate how machining errors influence gear pair meshing process, but also to study influence mechanism of single machining error. The proposed method could be used to guide the anti-vibration design and accuracy design of gear pairs.

Key words:machining errors; gear pairs; dynamic meshing characteristics; contact finite element analysis; dynamic transmission error; angular acceleration

传动平稳、可靠性高等优点使齿轮传动系统广泛应用于机械、航空航天领域，其动力和运动通过轮齿共轭齿面间连续的相互作用而传递，动力学行为与制造误差密切相关[1-2]。因此，研究制造误差对齿轮副动态啮合特性的影响具有重要意义。

国内外学者对此进行了大量的实验研究，会田俊夫等[3]研究了齿轮精度与性能的关系，蔡康洪等[4]、葛藤等[5]、徐宇东[6]给出了制造误差对齿轮振动噪声影响的一些规律，广泛的实际工程应用也积累了丰富的设计经验。但实际齿轮曲面是多种形式误差的综合，实验研究方法不能说清单项误差影响齿轮传动的机理。另一方面，在航空航天领域中，出现了一些新型结构形式的齿轮，在高转速下会表现出很强的非线性特性，已有的实验数据、经验参数不再适用，再进行实验研究的成本高、难度大，需要通过数值方法进行研究。

目前，制造误差影响齿轮副动态啮合特性的数值研究方法主要有三种。

一是从冲击理论的角度出发，由啮合基节误差计算啮合冲击力，通过建立分析模型和力学模型计算冲击作用下的动态响应。王玉芳等[7]、姚文席等[8]利用该方法研究了由啮合冲击产生的齿轮振动，详细讨论了各种误差对加速度噪声的影响。

二是将齿轮系统作为弹性的机械振动系统，通过建立齿轮轴系的有限元模型，利用弹簧模型模拟齿轮副的啮合刚度，把制造误差引起的静态传递误差STE(Static Transmission Error)作为激励，求解系统的动态响应。Ozguven等[9]利用该方法研究了STE对高速齿轮动态特性的影响，Kahraman[10]进行了多级齿轮的动态响应。

三是以弹性接触动力学基本理论为基础，利用静态接触有限元研究制造误差对齿轮副啮合状态的影响。林腾蛟等[11]、Li等[12-13]利用该方法研究了制造误差对轮齿接触强度和弯曲强度的影响。

上述研究方法基于大量简化和假设研究了制造误差对齿轮振动噪声的影响，要么将其当作单纯的位移激励要么只能研究某种状态下的齿轮受力情况，而不能具体描述制造误差对齿轮共轭齿面啮合过程的影响。因此，有必要提出一种数值方法，能够在不对传动结构进行简化和假设的前提下，研究制造误差对齿轮副连续啮合过程的影响。吴勇军等[14-18]提出了一种基于接触有限元的高保真动力学分析方法，可以考虑啮合过程中的时变刚度、滑动摩擦等多种因素，并通过实验验证了其有效性，但研究过程中均将齿廓假设为理想的标准渐开线齿廓。本文将在这种分析方法的基础上研究制造误差对齿轮副动态啮合特性的影响。

首先基于几种典型制造误差的结构形式提出了一般的建模方法，利用接触有限元分析方法进行啮合过程仿真，对比分析了理想齿轮副和含误差齿轮副的角速度、接触力特性。然后对单项误差的影响进行研究，分别以齿廓误差和齿距误差为对象，利用傅里叶变换量化分析了单项制造误差对齿轮副动态传递误差、角加速度特性的影响规律，讨论了单项误差影响齿轮振动的机理，并得到一些重要结论。

1制造误差与建模方法

齿轮制造误差主要来源于机床传动链的周期误差和刀具误差，在《渐开线圆柱齿轮精度标准》中，根据各项加工误差对使用性能的影响，将齿轮公差划分为3组，已有研究表明[4-5]：对齿轮啮合状态影响较大的公差项主要有齿形误差、周节误差和基节误差，其他公差项则影响不大。限于篇幅，只讨论以上3种误差的形式特点。

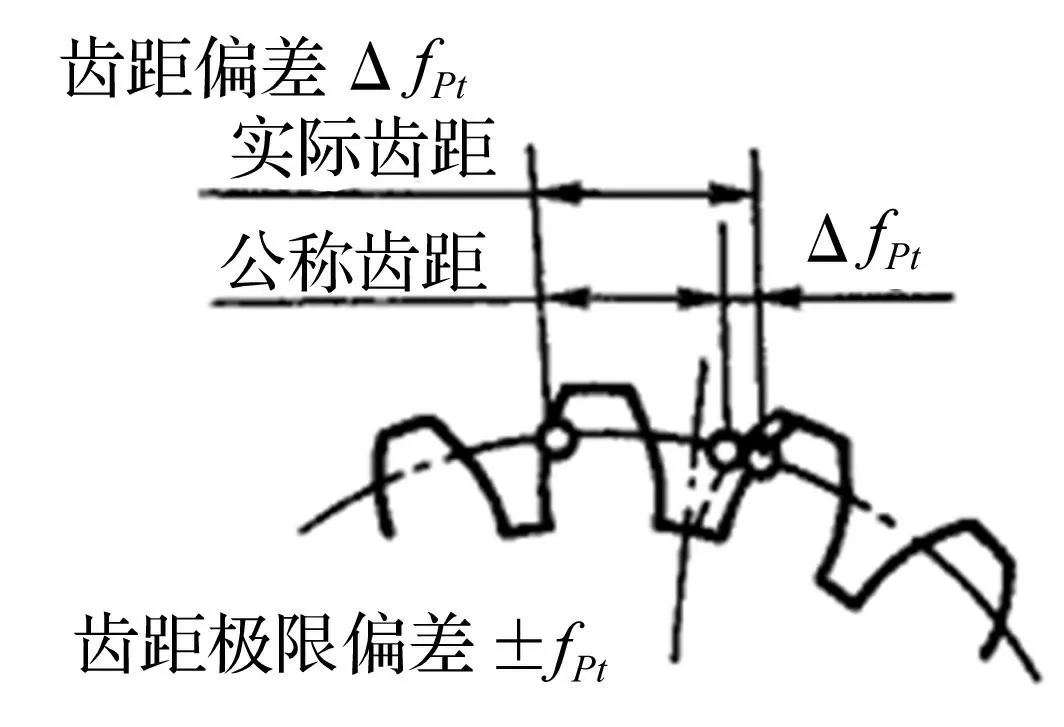
图1　齿距偏差示意图 Fig.1 Definition of pitch deviation

图2　基节偏差示意图 Fig.2 Definition of base circle pitch deviation

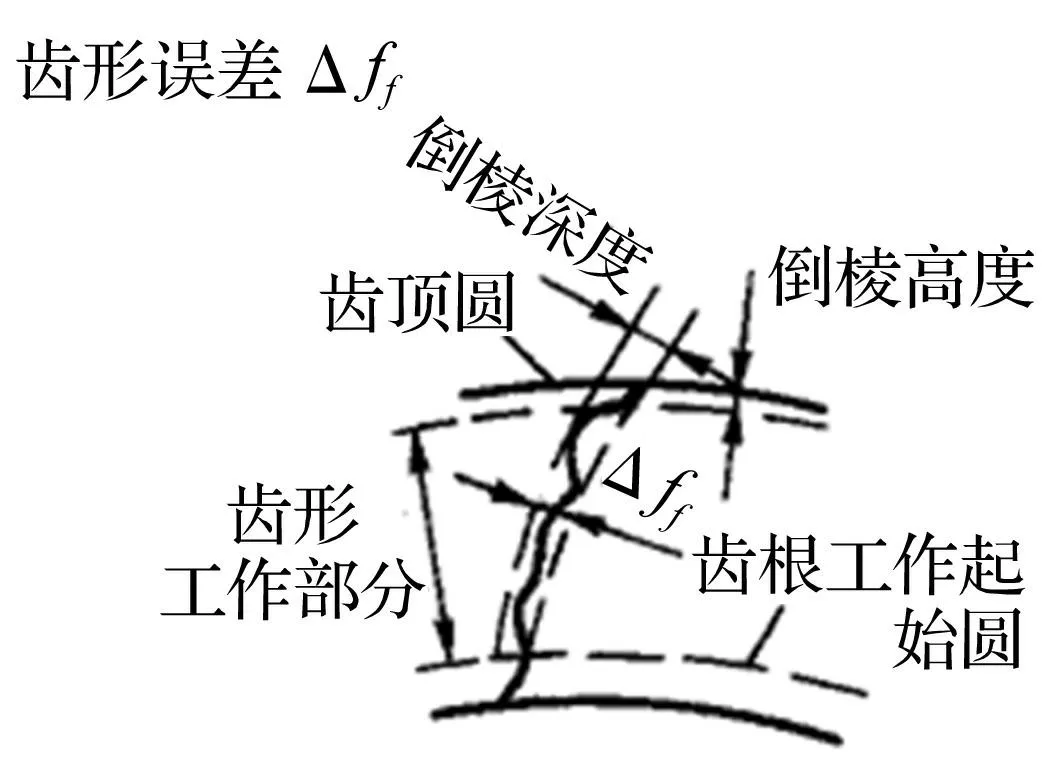
图3　齿形误差示意图 Fig.3 Definition of profile deviation

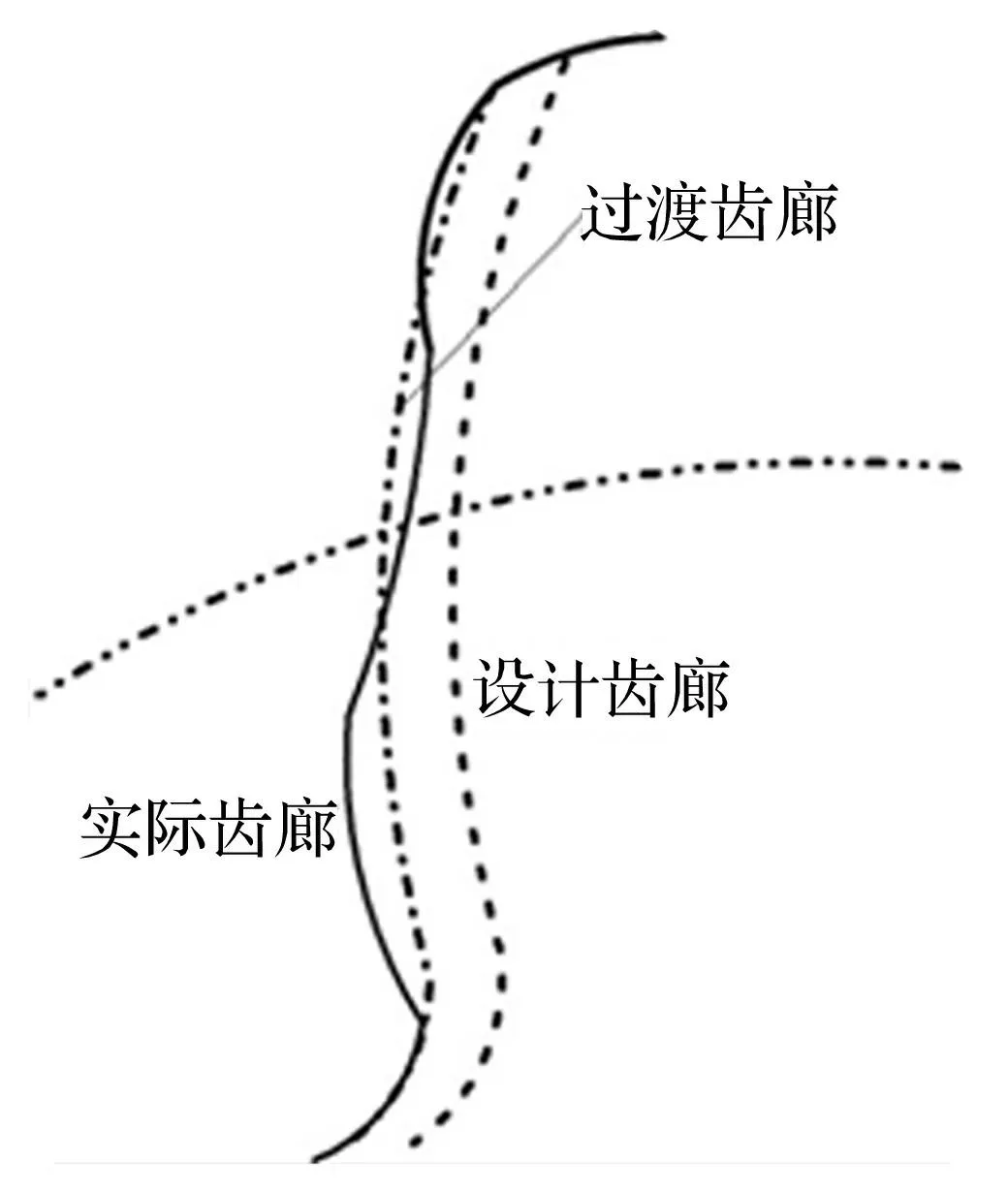
图4　制造误差示意图 Fig.4 Definition ofmachining error

(1)齿距误差：在分度圆上的实际齿距与公称齿距之差，如图1所示。该项误差本质是实际齿廓在圆周方向的位置偏差，理想啮合位置的偏移会破坏齿轮副啮合状态。

(2)基节误差：实际基节与公称基节之差，如图2所示。形式特点与齿距偏差类似。

(3)齿形误差：在端截面上，齿形工作部分内，包容实际齿形且距离为最小的两条设计齿形间的法向距离，如图3所示。该误差产生的原因是实际加工的整条齿形曲线凹凸不平，与光滑的设计齿形曲线发生了偏差，因此该误差的本质是实际齿形与设计齿形在形状上的差异。

分析结果表明，几乎所有制造误差项均可看成如图4所示的两种偏差的合成，一种是理想齿廓(虚线)在圆周方向上至过渡齿廓(点划线)的偏移，称为齿距偏差；另一种是过渡齿廓与实际齿廓(实线)在形状上的偏差，称为齿廓偏差[1]。

根据上述认识，实际齿轮的制造误差建模可以分为两步。第一步是进行理想齿廓在圆周方向的偏移，按照检测报告中的各齿实际偏差值进行偏移得到含齿距误差的过渡齿廓；第二步是生成实际齿廓，根据齿廓曲线检测报告，将过渡齿廓的各点在法线方向上进行相应偏差值的偏移，即可得到含齿距误差和齿廓误差的实际齿廓。完成实际齿廓建模后，沿实际螺旋线拉伸即可得到相应的齿轮模型。

这种建模方法不需要进行简化和假设，可以真实模拟任意形式、大小的制造误差。得到的高保真几何模型中的制造误差连续分布在整个共轭齿面上，如图4所示，并作为连续的位移激励影响齿轮副整个啮合过程。

2接触有限元建模及分析方法

2.1啮合齿轮副有限元建模

齿轮制造误差量级较小，为避免数值误差等因素，本文利用APDL语言直接在商用有限元软件ANSYS中进行几何建模和网格划分。以一对渐开线直齿轮副为例[16]进行分析，主要参数见表1。首先假设各轮齿齿距偏差在公差带内随机分布，如图5所示；齿廓各点与理想齿廓的形状偏差按正弦分布，如图6所示。基于第1节提出的方法进行建模。实际齿轮建模时无需进行假设，按照检测报告建模即可然后利用8节点六面体单元对齿轮副实体模型进行离散，得到如图7所示的啮合齿轮副有限元模型，该模型共计65 664个实体单元。为便于施加载荷和约束，在轮体内圈建立共计3456个壳单元，并将其钢化，具体为：约束主、从动轮内圈结点绕其轴线的转动自由度以外的其他所有自由度，在主动轮内圈壳单元上施加驱动转速Ω(314.15 rad/s)，在从动轮内圈壳单元上施加负载扭矩M(143.6 N·m)。

表1　直齿轮副主要参数

图5　齿距偏差分布 Fig.5 Distribution of pitch deviation

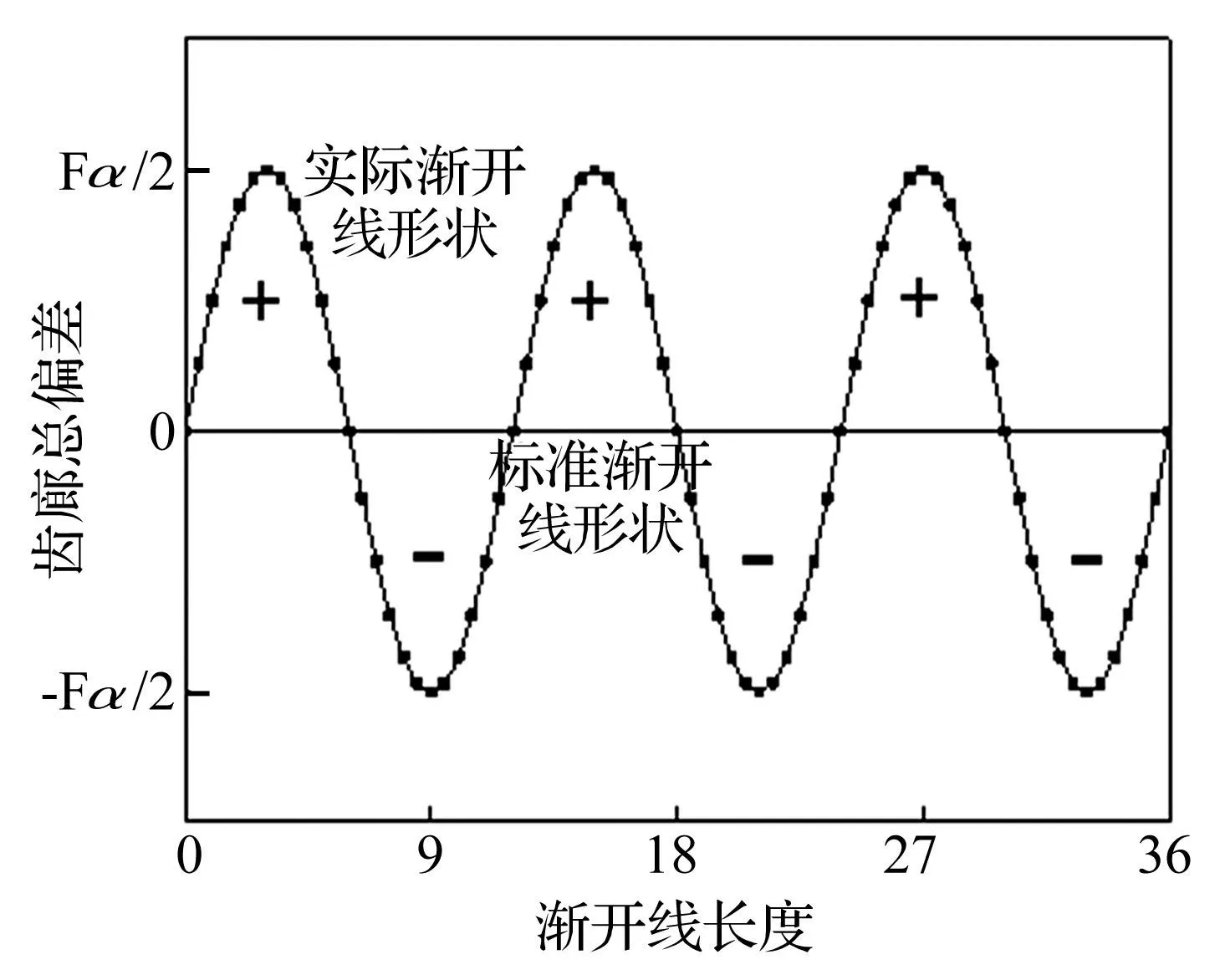
图6　齿廓偏差分布 Fig.6 Distribution of profile deviation

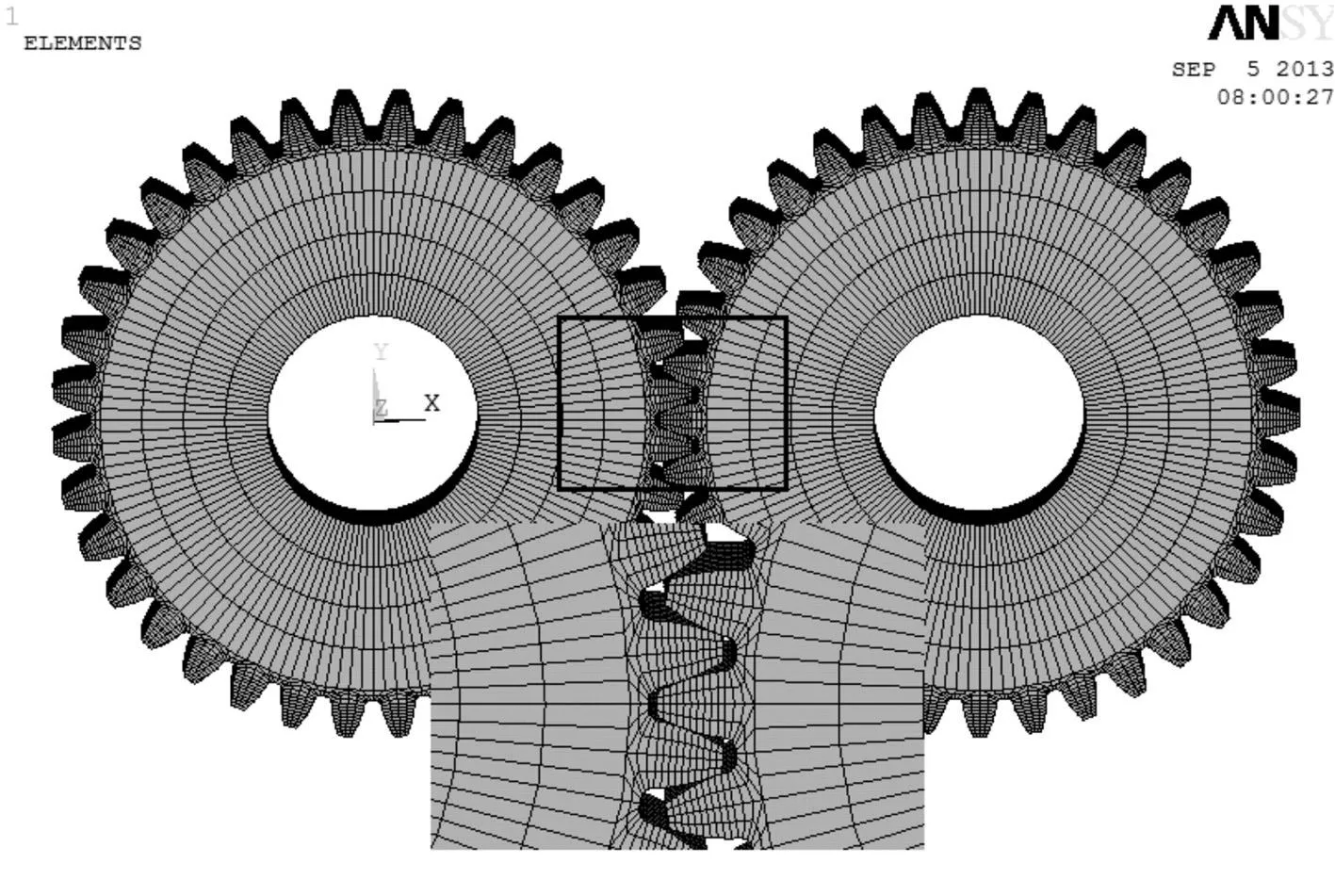
图7　啮合齿轮副有限元模型 Fig.7 FE model of engaged gear pairs

2.2啮合过程接触有限元分析

在已建立精确的啮合齿轮副有限元模型基础上，可进行齿轮副啮合过程的有限元分析。该方法在文献[14-18]中进行了详细叙述，这里只做简单介绍。

由啮合原理可知，齿轮副每一时刻的接触状态与之前时刻的接触状态以及齿廓线的实际几何形状密切相关，且可以根据前面的已知接触状态进行确定，为了分析齿轮副连续啮合过程中的动态特性，须求得齿轮副连续啮合过程中每个时刻的动力学参数。

首先将齿轮副整个啮合过程离散成时间序列：0,Δt,2Δt,…,t,t+Δt,…,T，其中某一时刻t的动态接触模型如图8所示。然后根据虚位移原理利用更新拉格朗日格式的增量形式分别建立动力学方程，任一时刻主、从动齿轮的运动方程可表示为：

(1)

其中:

(2)

(3)

(4)

图8　齿轮副动态接触模型 Fig.8 Dynamic contact model of gear pairs

时刻t和时刻t+Δt通过接触力相互联系，利用罚函数可以求解啮合过程的等效接触力向量t+ΔtFC为

(5)

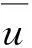
在分析得到齿轮副动态啮合过程的动力学方程及等效结点接触力向量t+ΔtFC后，将t+ΔtFC代入动力学方程(1)即可进行方程的求解。本文利用Ls-Dyna软件采用二步形式的中心差分法对各时刻进行求解，得到了整个啮合过程的各个力学参量。

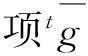
在齿轮副啮合过程中，任意时刻t处的制造误差通过改变此时接触点对间的相对位移影响接触力t+ΔtFC，然后作为激励和时刻t的啮合状态一起决定了时刻t+Δt的动力学响应，这就是制造误差影响齿轮副啮合过程的机理描述。

3齿轮副动态啮合过程分析

分别对理想的啮合齿轮副有限元模型和含制造误差的啮合齿轮副有限元模型进行动力学求解，提取系统响应进入稳态后的动态接触力、从动轮角速度信号，对比分析制造误差对啮合过程的影响。

研究表明[1]，具有时变刚度激励的齿轮系统是一类典型的参数振动系统，其动态响应具有一般参数振动系统的响应特性，可根据齿轮副的基本参数得到齿轮副扭转振动的平均等效频率为2 409 Hz左右，啮合频率为1 800 Hz[18]。

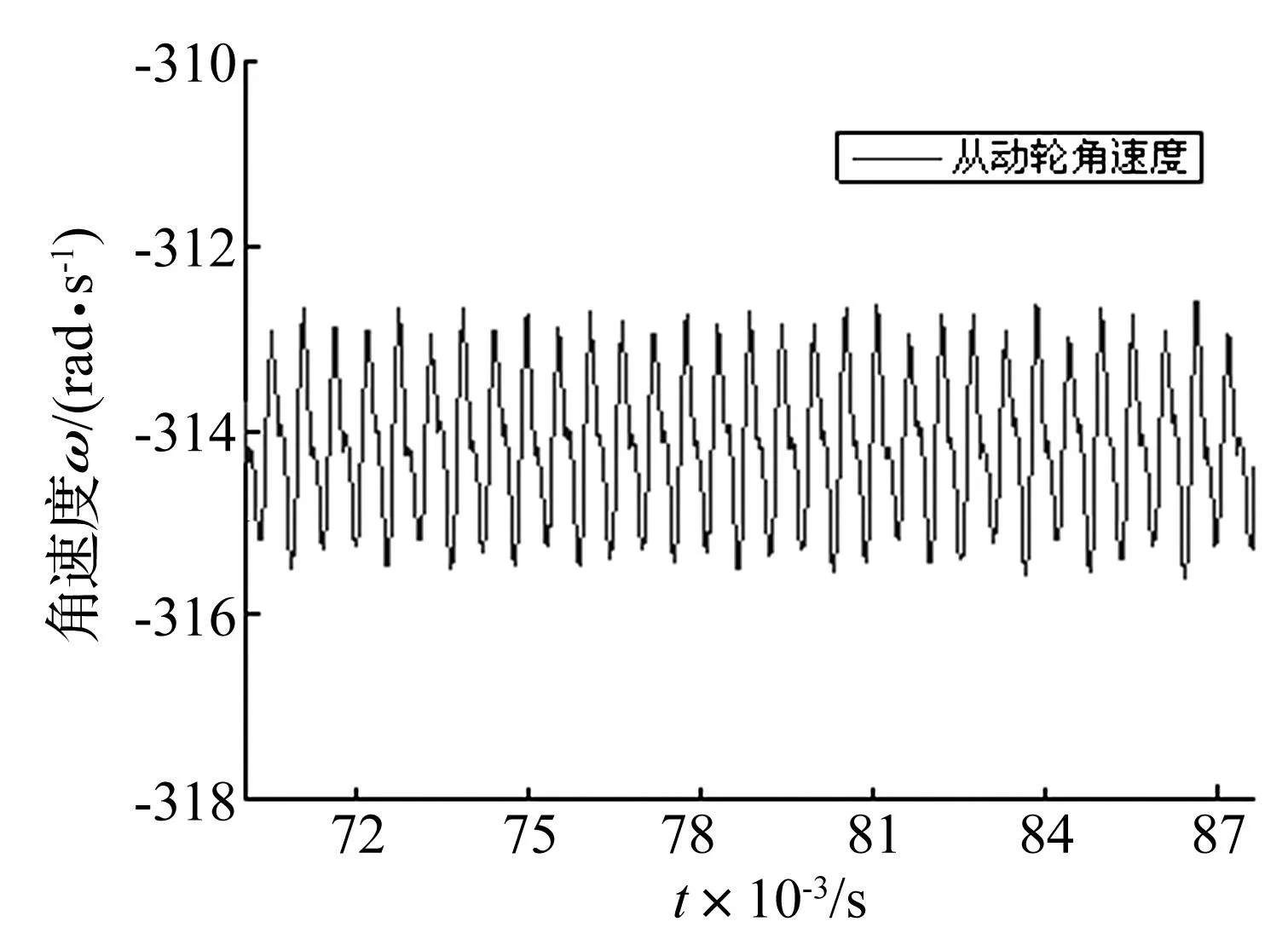
图9　理想齿轮副角速度响应 Fig.9 Angular velocity of driven gear without error

图9为理想齿轮副从动轮的时域角速度响应信号，图10为含齿廓误差的从动轮角速度响应信号。两图中的曲线波动周期均为0.55 ms，与啮合周期一致；均值同为设计角速度，只是后者波动幅值接近前者的2倍，这是因为制造误差的存在增大了系统激励，在系统刚度几乎不变的情况下，从动轮角速度波动更加剧烈。

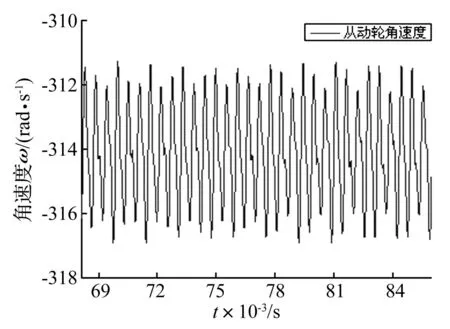
图10　含齿廓误差齿轮副角速度响应 Fig.10 Angular velocity of driven gear with profile error

图11为理想齿轮副的动态接触力响应信号，图12为含齿距误差的齿轮副动态接触力响应信号。图11中，轮齿弹性变形引起的啮合冲击使动态接触力在均值(扭矩/作用半径)上下波动；而由于齿距误差的存在，图12的接触力波动范围急剧增加，出现了0 N和9 000 N，这对应了齿轮副啮合过程中的“脱齿”和“双边啮合”现象。还可以发现，前者的曲线波动周期为0.55 ms，与啮合周期一致；后者曲线波动周期则为0.42 ms，该频率恰好是齿轮副扭转振动的平均等效频率，说明此时的主导振动为齿轮副的扭转振动。

图11　理想齿轮副动态接触力 Fig.11 Contact force of gear pairs without error

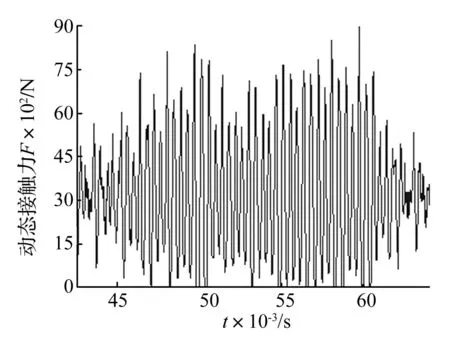
图12　含齿距误差齿轮副动态接触力 Fig.12 Contact force of gear pairs with pitch error

通过上述分析可以发现，制造误差的引入对齿轮副啮合过程产生了较为显著的影响，不仅会导致齿轮振动、动态接触力的增大，在一定情况下还会改变振动响应的主导频率成分。因此，本文提出的建模方法和有限元分析方法是可行的，能够描述制造误差影响齿轮副啮合过程的作用机理，而且不会因为量级较小而被忽略掉。

4单项制造误差对啮合特性的影响

传统实验方法只能对综合误差进行研究，而本文提出的这种方法则可对任意形式的误差形式进行建模，如果只模拟一种形式的制造误差，就可以分析单项制造误差影响齿轮啮合的机理，开展这种研究可以弥补传统实验方法的不足。

通过显示积分的接触有限元分析方法能够求解啮合过程中任意时刻的动力学参数，不仅可以对单项制造误差作用下的齿轮副啮合过程进行描述，还能对各种啮合特性进行定量分析，如加速度、速度和应力等。

本文选取动态传递误差和角加速度两种特性作为评价指标进行对比分析。其中动态传递误差DTE(Dynamic Transmission Error)物理意义为齿轮副实际角位移与理论角位移的偏差，能够直接反映齿轮副传动的准确性，并且也是齿轮振动、噪声产生的根源；角加速度则与齿轮副的振动噪声密切相关[16-18]，工程中常用该指标进行齿轮振动评价。

首先按表2所示的齿轮精度表[19]进行含单项误差的啮合齿轮副有限元建模，不同精度等级下的齿轮仅存在误差大小的差异，误差分布形式等均保持一致。然后基于接触有限元方法进行啮合过程仿真，提取DTE和角加速度的时域响应信号，并利用快速傅里叶变换技术将时域响应信号转换到频域进行分析，研究齿轮振动的主要频率成分和对应的响应幅值，定量分析制造误差对啮合特性的影响，进而讨论单项制造误差影响齿轮振动的作用机理。

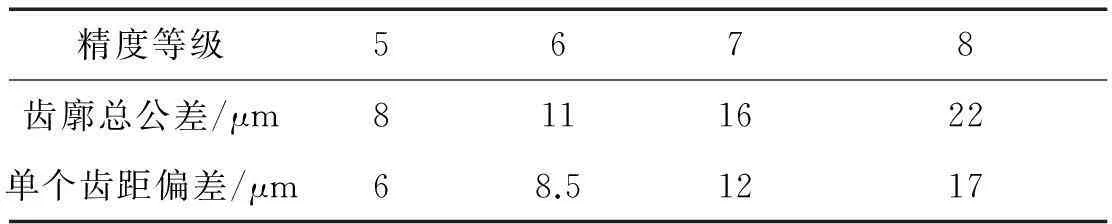
表2　齿轮精度数值表

4.1理想齿轮副啮合特性分析

对理想齿轮副啮合时的动态传递误差和从动轮角加速度时域信号进行频谱分析如图13、图14所示，其频率成分主要为啮合频率f0及其2倍频2f0。另外，在2 500 Hz处由于激起了齿轮副扭转振动，振动响应幅值较大；10 795 Hz处则是啮合频率的6倍频激起了单个齿轮的弯曲振动，但因为6阶的谐波分量较小，振动响应幅值也就不大。

因此，在利用Campbell图进行齿轮共振分析时，啮合频率及其倍频不仅要避开单个齿轮的低阶固有频率，还要避开扭振固有频率才能有效防止共振的发生。

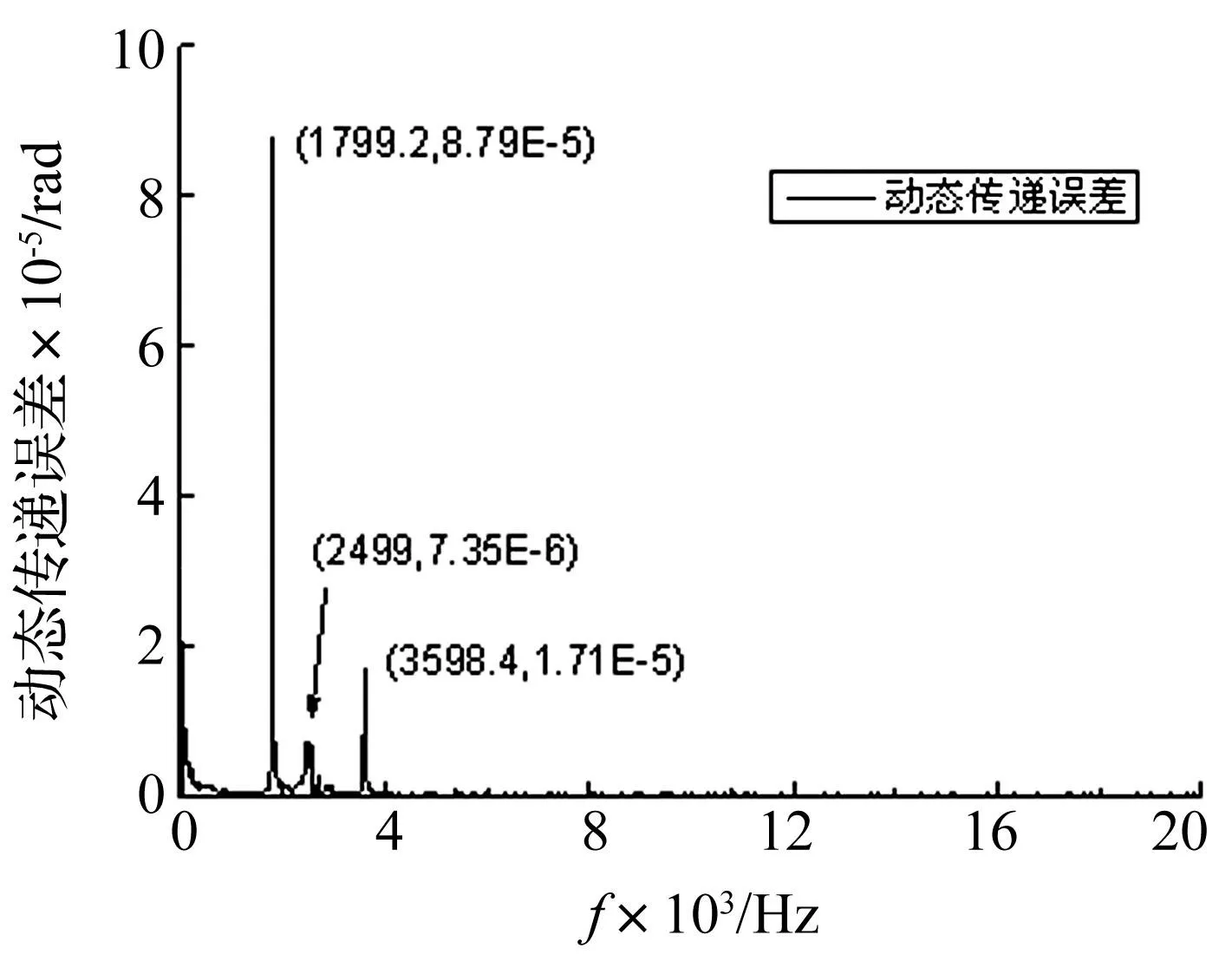
图13　理想齿轮副动态传递误差频谱 Fig.13 DTE response of gear pairs without error

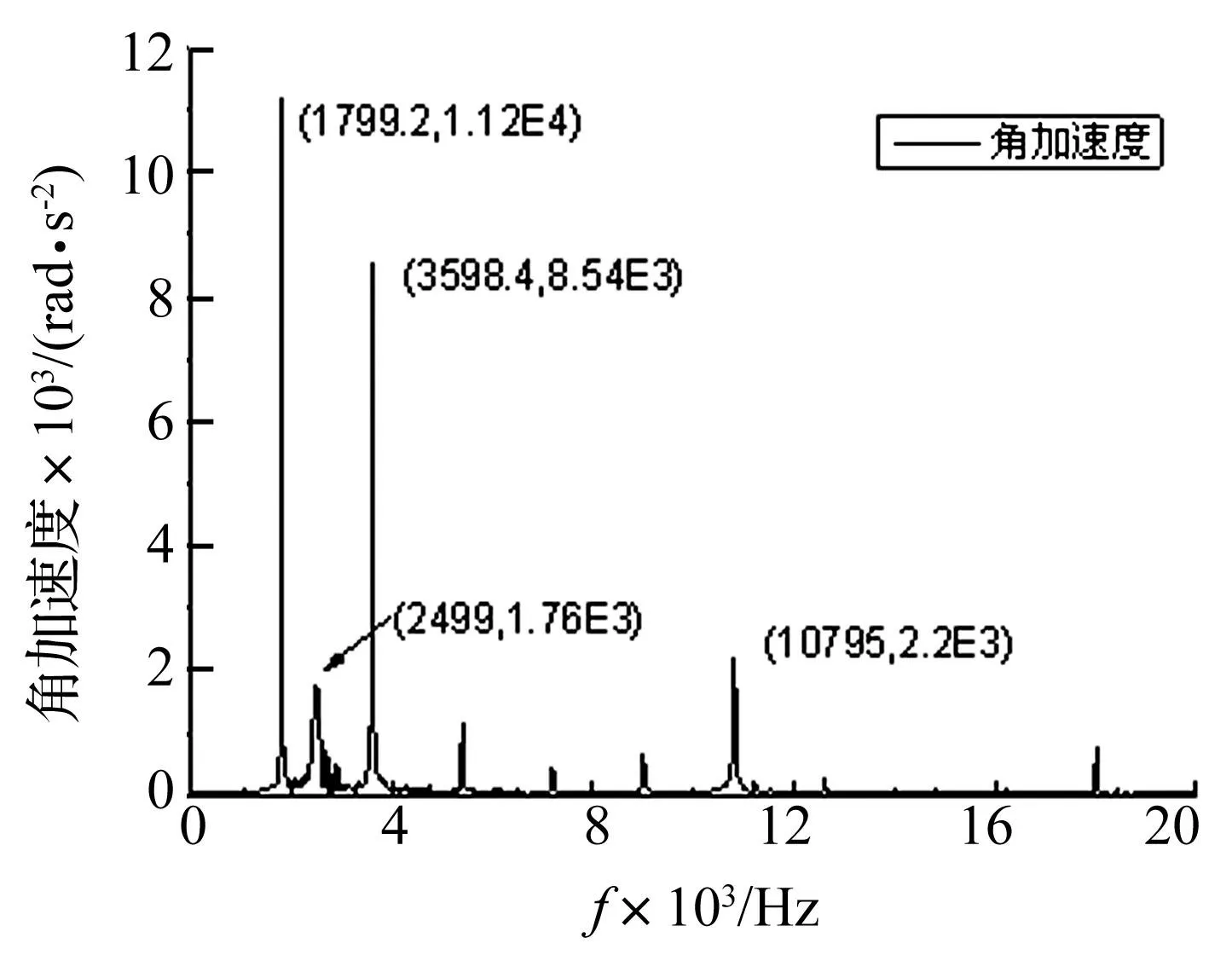
图14　理想齿轮副角加速度频谱 Fig.14 Angular acceleration response of gear pairs without error

4.2齿廓误差对啮合特性的影响

图15、16分别为加工精度8级的含齿廓误差齿轮副DTE、角加速度响应特性频谱图。不同公差等级下，齿廓偏差对齿轮副啮合特性的影响规律见表3和表4。综合分析图15、16和表3、4可以发现：

图15　含齿廓误差的齿轮副动态传递误差频谱 Fig.15 DTE response of gear pairs with profile error

(1)在引入齿廓误差后，齿轮副整体响应特性和理想齿轮副相比变化不大，仍以啮合频率及其2倍频为主；

(2)随齿廓偏差的增大，齿轮副DTE、角加速度响应在主要频率成分处幅值增加，当加工精度较低时，齿廓偏差取代轮齿弹性变形成为响应齿轮振动的主要因素；

(3)齿轮系统本质上是参数振动系统，齿廓误差的引入改变了齿轮副的时变啮合刚度分布，随齿廓误差的增大，扭振频率有所降低。

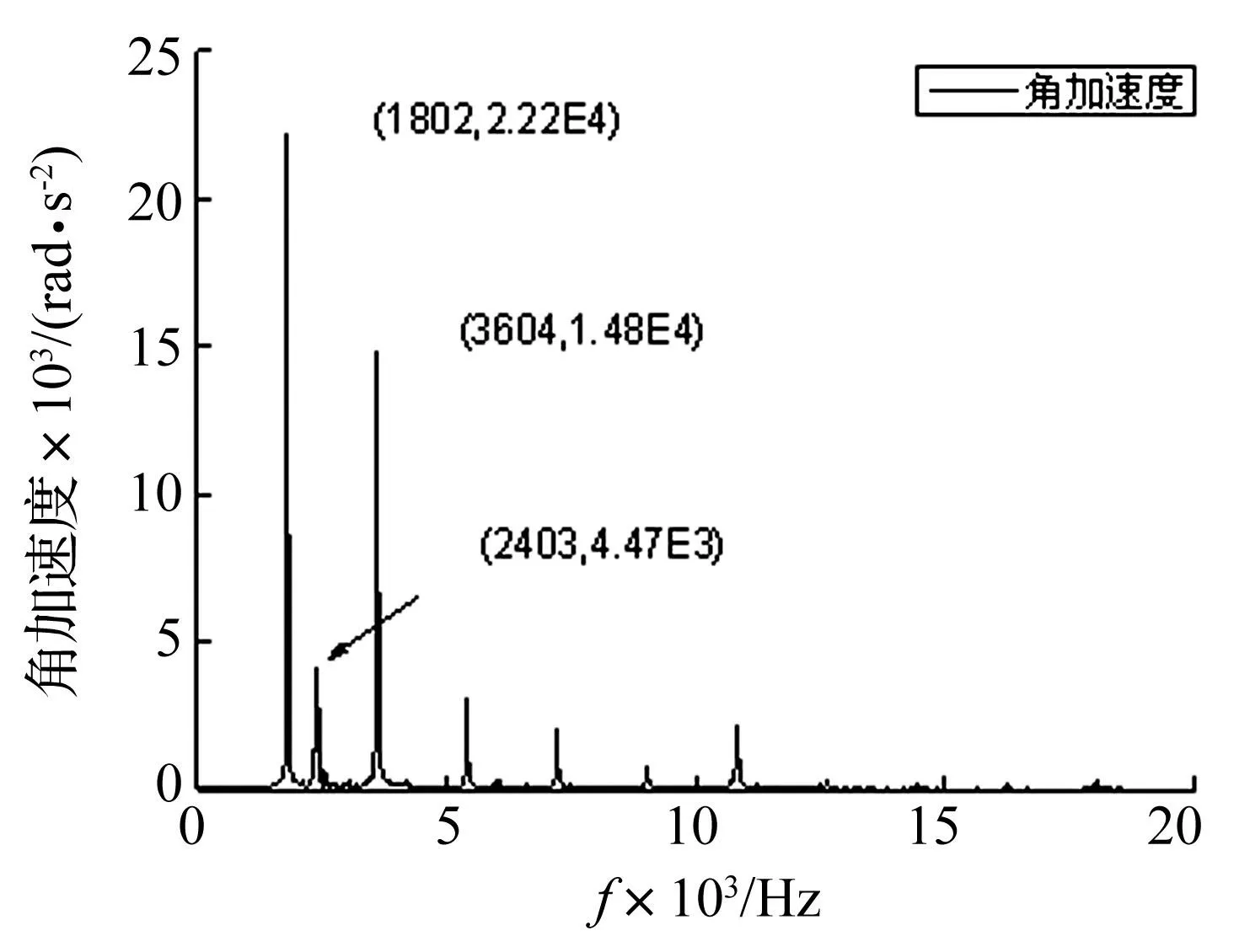
图16　含齿廓误差的齿轮副角加速度频谱 Fig.16 Angular acceleration response of gear pairs with profile error

公差等级无误差5678扭振频率24982494249724502402(Hz)及幅值7.4E-61.7E-52.8E-52.4E-51.8E-5f0处幅值8.8E-51.2E-41.3E-41.5E-41.7E-42f0处幅值1.7E-52.3E-52.5E-52.8E53.0E-5

表4　不同齿廓偏差的齿轮副角加速度响应(rad/s 2)

4.3齿距误差对啮合特性的影响

图17、18分别为加工精度5级的含齿距误差齿轮副DTE、角加速度响应特性频谱图。不同公差等级下，齿距偏差对齿轮副啮合特性的影响规律见表5和表6。

表5　不同齿距偏差的齿轮副DTE响应(rad)

图17　含齿距误差的齿轮副动态传递误差频谱 Fig.17 DTE response of gear pairs withpitch error

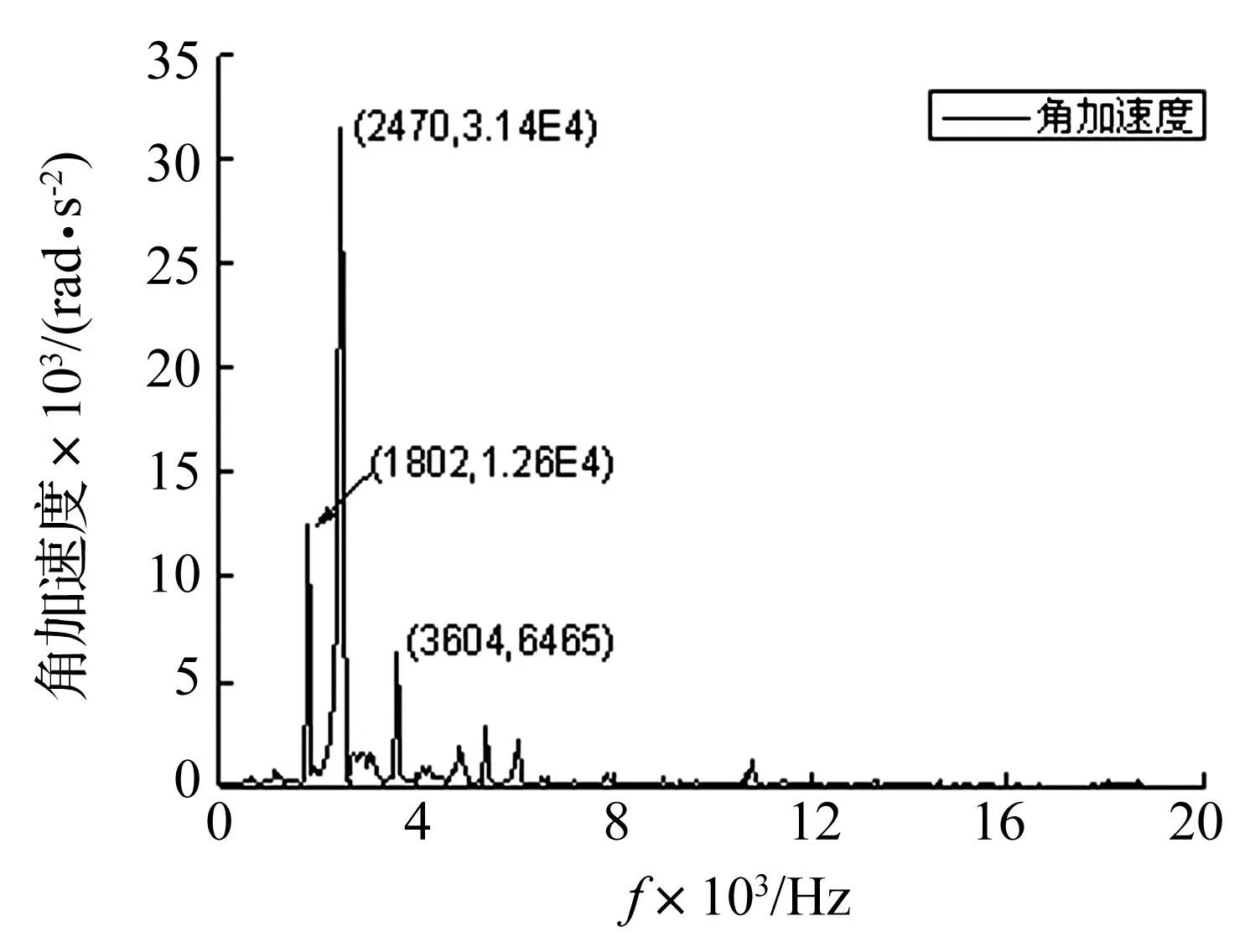
图18　含齿距误差的齿轮副角加速度频谱 Fig.18 Angular acceleration response of gear pairs withpitch error

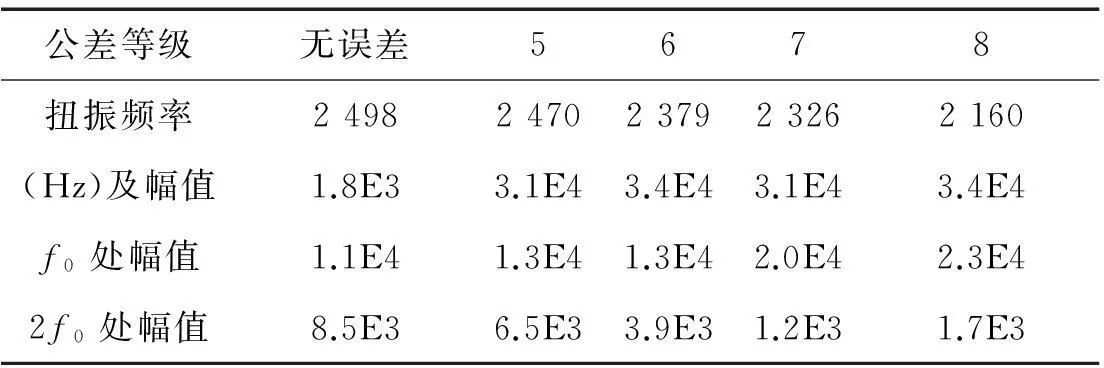
公差等级无误差5678扭振频率24982470237923262160(Hz)及幅值1.8E33.1E43.4E43.1E43.4E4f0处幅值1.1E41.3E41.3E42.0E42.3E42f0处幅值8.5E36.5E33.9E31.2E31.7E3

综合分析图17、18和表5、6可以发现：

(1)在引入齿距偏差后，齿轮副整体响应特性发生了较大变化，扭振频率处响应迅速增加，成为主导振动之一；

(2)齿距误差的存在破坏了齿轮的连续啮合状态，尤其是在轮齿啮合交替处会产生巨大的啮合冲击，并可能伴随“脱齿”和“双边冲击”，引起齿轮振动的迅速增大。

(3)随齿距误差增加，齿轮副扭振频率有所降低，2倍频响应逐渐减小，振动响应成分以啮合频率和扭振频率为主。

因此，本节的研究表明不同形式的制造误差对齿轮振动的影响机理不同。齿廓误差“平稳”地影响整个啮合过程，使振动有所增加，而齿距误差则是影响齿轮副的啮入啮出瞬间，引起啮合状态的突变，并可能会产生“脱齿”和“双边啮合”等现象，甚至激起齿轮副的扭转振动。

接触有限元方法能够对齿轮副啮合特性进行定量分析，不仅可以通过与理想齿轮副对比得到影响齿轮振动的主要因素用来指导齿轮的减振实际，还能评价不同加工精度下的齿轮振动大小用于指导齿轮的精度设计。

另一方面，齿轮副扭转振动是一个参数振动问题，共振频率与啮合刚度关联密切，制造误差的存在改变了接触点对间相对位移，对啮合刚度造成了一定的影响，扭振频率随之发生变化。

5结论

通过上述研究得到以下几点结论：

(1)本文提出的建模方法可以对任意形式的制造误差进行模拟，模型中的制造误差连续分布在整个齿廓上；

(2)基于接触有限元的动力学分析方法可以描述制造误差对整个连续啮合过程的影响，可对单项误差影响齿轮振动的作用机理进行研究；

(3)该方法能够定量研究各种啮合特性，研究结论可用于指导齿轮的减振设计和精度设计；

(4)齿轮在进行共振分析时，还应考虑齿轮副的扭转振动形式。

参考文献

[1]李润方，王建军. 齿轮系统动力学[M]. 北京：科学出版社，1997.

[2]Smith J D. Gear noise and vibration [M]. Marcel Dekker Inc, New York, 2003.

[3]会田俊夫. 齿轮的精度与性能[M]. 北京：中国农业机械出版社，1985.

[4]蔡康洪，章宋诚. 齿轮误差对齿轮噪声的影响[J]. 工具技术，1980(6)：18-25.

CAI Kang-hong, ZANG Song-cheng. The influence of machining errors on gear noise[J]. Tool Engineering, 1980(6)：18-25.

[5]葛藤，宫镇，王仲章. 齿轮及齿轮箱噪声、振动研究的现状[J]. 噪声与振动控制，1989,9(1)：26-30.

GE Teng, GONG Zheng, WANG Zhong-zang. The vibration and noise research situation of gear and gear box[J]. Noise and Vibration Control, 1989,9(1)：26-30.

[6]徐宇东. 轿车变速箱齿轮噪声与制造误差关系的作用机理分析和试验研究[D]. 吉林：吉林大学，2010.

[7]王玉芳，童忠钫. 齿轮误差对齿轮加速度噪声的影响[J]. 振动、测试与诊断，1993(4)：5-14.

WANG Yu-fang, DONG Zhong-fang. The influence of machining errors on the gear acceleration noise[J]. Journal of Vibration, Measurement & Diagnosis, 1993(4)：5-14.

[8]姚文席，魏任之. 渐开线直齿轮的啮合冲击研究[J]. 振动与冲击，1990,9(4)：57-61.

YAO Wen-xi, WEI Ren-zhi. The meshing impact study of involute spur gear[J]. Journal of Vibration and Shock，1990,9(4)：57-61.

[9]Ozguven, Houser D R. Dynamic analysis of high-speed gears by using loaded static transmission error [J]. Journal of Sound and Vibration, 1988,125(1)：71-83.

[10]Kahraman A. Dynamic analysis of a multi-mesh helical gear Train. Journal of mechanical design [J].1994,116: 706-712.

[11]林腾蛟，杨妍妮，李润方，等. 弧齿锥齿轮传动内部动态激励数值仿真[J]. 重庆大学学报，2009(6)：609-613.

LIN Teng-jiao, YANG Yan-ni, LI Run-fang, et al. Numerical simulation of the internal dynamic excitation of a spiral bevel gear transmission[J]. Journal of Chongqing University, 2009(6)：609-613.

[12]LI Shu-ting. Effects of machining errors, assembly errors and tooth modifications on loading capacity, load-sharing ratio and transmission error of a pair of spur gears [J]. Mechanism and Machine Theory, 2007, 42(6): 698-726.

[13]LI Shu-ting. Finite element analyses for contact strength and bending strength of a pair of spur gears with machining errors, assembly errors and tooth modifications [J]. Mechanism and Machine Theory, 2007, 42(1): 88-114.

[14]吴勇军，王建军. 一种考虑齿轮副连续啮合过程的接触有限元动力学分析方法[J]. 航空动力学报，2013(5)：1192-1200.

WU Yong-jun,WANG Jian-jun. A contact finite element method for dynamic analysis of continuous engaged gear pairs [J]. Journal of Aerospace Power, 2013(5)：1192-1200.

[15]吴勇军，王建军，韩勤锴，等. 基于接触有限元分析的斜齿轮齿廓修形与实验[J]. 航空动力学报，2011(2)：409-415.

WU Yong-jun,WANG Jian-jun,HAN Qin-kai,et al. Tooth profile modification of helical gears and experimental study based on finite element contact analysis[J]. Journal of Aerospace Power, 2011(2)：409-415.

[16]WU Yong-jun，Wang Jian-jun，HAN Qin-kai. Contact finite element method for dynamic meshing characteristics analysis of continuous engaged gear drives [J]. Journal of Mechanical Science and Technology, 2012, 26(6): 1671-1685.

[17]WU Yong-jun，Wang Jian-jun，HAN Qin-kai. Static/dynamic contact FEA and experimental study for tooth profile modification of helical gears [J]. Journal of Mechanical Science and Technology, 2012, 26(5): 1409-1417.

[18]吴勇军，梁跃，杨艳，等. 齿轮副动态啮合特性的接触有限元分析[J]. 振动与冲击，2012,31(19)：61-67.

WU Yong-jun，LIANG Yue, YANG Yan, et al. Dynamic meshing characteristics study of gear pairs using contact finite element analysis method [J]. Journal of Vibration and Shock，2012,31(19)：61-67.

[19]机械设计手册委员会. 机械设计手册-齿轮传动[M]. 北京：机械工业出版社，2007.