基于时频滤波的汽轮机半速涡动故障成分提取

第一作者滕伟男，博士，副教授，1981年8月生

基于时频滤波的汽轮机半速涡动故障成分提取

滕伟，安宏文，马志勇，柳亦兵

(华北电力大学能源动力与机械工程学院，北京102206)

摘要：汽轮机油膜涡动是滑动轴承失稳而产生的自激振动，其振动频率主要表征为转子转频的一半或略小。当油膜涡动频率等于转子一阶临界转速时会导致振动加剧，进而对汽轮机的稳定运行产生严重影响。Gabor变换是一种可逆的联合时频分布方法，其逆变换具有时域信号重构的能力。基于Gabor变换对850 MW汽轮机振动信号进行时频分析，显示反映轴系不稳定的半速涡动成分，进一步对该成分进行时频带通滤波，并基于Gabor逆变换予以时间重构，获取半速涡动成分的峰峰值量化指标，为汽轮机轴承油膜涡动故障提供诊断依据。

关键词：半速涡动；Gabor变换；时频滤波；故障成分提取

基金项目：国家自然科学基金资助项目(51305135);北京高等学校青年英才计划项目(YETP0701);中央高校基本科研业务费项目(12MS06)

收稿日期：2013-10-09修改稿收到日期：2014-03-03

中图分类号:TH212；TH213.3文献标志码：A

Semi-speed oil whirl fault component extraction in a steam turbine based on time-frequency filtering

TENGWei，ANHong-wen，MAZhi-yong，LIUYi-bing(School of Energy, Power and Mechanical Engineering, North China Electric Power University, Beijing 102206, China)

Abstract:Oil whirl of a steam turbine is a self-excited vibration, it is caused by instability of sliding bearings. Its vibration frequency is denoted with half of the rotational frequency of a rotor shaft or less. Once the frequency of oil whirl is equal to the first critical speed of the rotor shaft, the vibration of the steam turbine is intensified and its stability may be destroyed. Gabor transformation is a reversible joint time-frequency distribution method, its inverse transform has an ability of time domain signals reconstruction. Here, the vibration signals of a 850 MW steam turbine were analyzed based on Gabor transformation, and the semi-speed oil whirl component representing instability was detected, then the semi-speed component was filtered using a band-pass filter in time-frequency domain and reconstructed using inverse Gabor transformation. At last, a peak-to-peak quantified index was calculated to judge the level of oil whirl. The proposed method provided a guide for oil whirl fault diagnosis of steam turbines.

Key words:semi-speed oil whirl; Gabor transformation; time-frequency filtering; fault component extraction

汽轮机油膜涡动是一种由于滑动轴承失稳而产生的自激振动[1-2]，随着转速升高，涡动的半速特性可能与转子的一阶临界转速耦合，产生共振，不仅造成发电机组各部件的松动与疲劳，严重时发生轴瓦磨损、烧伤甚至机组失稳、轴系破坏等后果[3-4]。因此，基于汽轮机振动监测信号，分析油膜涡动的故障机理，获取振动特征并进行故障定位，对于及早发现涡动故障、制定相应保护对策具有重要意义。

滑动轴承油膜涡动的机理研究是汽轮机振动领域的基础性工作：文献[5-6]针对径向轴承的流固耦合特性，探讨了轴颈半速涡动的机理，给出了涡动动力学行为的非线性特征；Bachschmid等[7]建立了半速涡动不稳定状态下的动力学模型，分析了实验模型与理论模型的矛盾之处。与此同时，针对涡动所致的不稳定运行的故障诊断技术也取得丰硕成果，文献[8-10]分析了不同转速下轴承涡动的频谱信息，揭示出相应的故障特征。然而随着汽轮机单机容量的大型化、机组结构的复杂化，常规的频谱分析方法难以适应振动信号的非平稳、非线性特点，对涡动所致不稳定振动的时间信息缺乏准确判断。近年来，随着信号处理新方法的不断涌现，文献[11]基于HHT方法分析了转子的油膜涡动与油膜振荡的故障特征，文献[12]基于阶比分析识别转子油膜涡动的故障频率，但上述研究针对的是转子试验台测试数据，对于处于高温高压环境、参与调峰变载运行的实际汽轮机油膜涡动故障研究不足。

Gabor变换是一种典型的时频分析方法，它可以理解为加高斯窗的短时傅里叶变换，在旋转机械的振动分析中得到广泛应用：文献[13-15]利用Gabor变换对振动信号进行阶比分析，研究了对偶函数双正交条件、邻近阶比和交叉阶比的分离等问题，并分别在航空发动机、转子试验台上进行验证；文献[16]基于Gabor变换进行盲源信号分离，突破了传统盲信号分离方法中要求源信号相互独立及源信号中最多只能有一个高斯信号的限制。

本文基于Gabor变换对850 MW汽轮机不稳定运行过程中的振动信号进行时频分析，显现产生不稳定故障的半速涡动成分，对时频平面内的振动信息进行带通滤波，基于Gabor逆变换对滤波后信号予以信号重构，获取反映不稳定运行的量化故障特征，并进行故障定位，为汽轮机的油膜涡动故障诊断提供依据。

1基于Gabor变换的时频分析

傅里叶变换只能反映信号在频域内的整体信息，难以对非平稳信号给出局部时间范围的谱信息描述，为此，Gabor提出一种加窗的傅里叶变换，用以获取在时频域不同尺度、不同方向上的相关特性[17]，工程上通常采用离散的Gabor变换进行振动信号分析。

1.1离散Gabor变换

Gabor变换是信号的一种非正交展开，离散Gabor展开定义为[18]

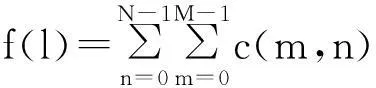
(1)

式中：f(l)为振动信号时间序列，数据长度为L；a为时频平面内的时间间隔，N为时间分段数，有L=aN；M为频率分段数；m、n分别为频域和时域样本点，γ(·)为窗函数的对偶函数。c(m,n)为Gabor展开系数，用信号的时间移位-频率调制二维表示，可用原始振动信号表示为

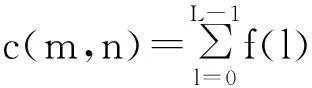
(2)

式中：g(·)为窗函数，与其对偶函数γ(·)满足如下关系

(3)

式中：F为频域间隔，δ.为脉冲函数。Gabor变换通常采用Gauss函数作为窗函数[19]，其与对偶函数的表达式为

(4)

(5)

式中：T为采样时间间隔。

1.2时频滤波与信号重构

Gabor展开系数可将振动信号表示成离散时间点和离散频率点的二维平面网格，在此平面网格内提取某阶振动成分的步骤如下：首先在起始时刻预估该阶振动成分的起始频率；然后依据各阶成分在时频平面的最小频率间隔，设定该阶成分的搜索带限；逐步选择每一时刻搜索带限内的最大值作为该成分的能量表示，如下式所示

(6)

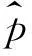
式(6)中，非频率索引处的幅值设为零，实现了时频域的信号滤波，将o(p,n)替换式(1)中的c(m,n)，即可得到该阶成分的时间重构信号。

2基于时频滤波的故障成分提取过程

(1)采集汽轮机原始轴振或瓦振信号；

(2)选择窗口函数g(t)，计算相应的对偶函数γ(t)；

(3)选择合适的时间间隔和频率间隔，将振动信号进行Gabor变换，即将一维时域信号转换为二维时-频表示；

(4)进行时频带宽内的峰值搜索，获取反映运行状态的某阶成分，即时频滤波；

(5)将滤波后的二维信号进行Gabor逆变换，重构时间信号；

(6)将重构后的时间信号归一化处理，得到峰峰值指标，如下式所示

(7)

式中：xp-p为重构信号的峰峰值。

3汽轮机振动信号分析

某火电厂850 MW大型汽轮发电机组由一个高压缸、一个中压缸和两个低压缸组成，主蒸汽温度535℃，主蒸汽压力18.2 MPa，工作转速为3000 r/min。机组配备申克公司的Turbine Supervisory Instrumentation (TSI)，用于连续监测机组转子振动(相对轴振)、轴承座振动(绝对瓦振)、胀差、轴位移、偏心、转速等运行参数，机组振动传感器布局如图1所示，在八个轴承座上各安装一个磁电式速度传感器，用于测量各个轴瓦处的绝对瓦振，输出为轴承座振动速度信号，单位为m/s；在八个轴承支承截面处成对安装电涡流位移传感器，用于测量转子相对于轴瓦的振动，输出为转子与轴瓦的瞬时相对位移，单位为μm，两个传感器之间成90°夹角布置，所有信号的采样频率为8 000 Hz。文中的振动分析基于图1中的1X、1Y、2X、2Y、3X、3Y、4X、4Y共八路轴振信号，如图2所示，高压缸两侧轴振(1X、1Y、2X、2Y)幅值较大但未超限，较大的振幅主要由于高压缸转子刚度较小所致，而中压缸和低压缸两侧(3X、3Y、4X、4Y)振幅相对较小。

图1　850 MW汽轮机结构及传感器布局 Fig.1 Structure of 850 MW steam turbine and placement of vibration transducers

图2　汽轮机相对轴振峰峰值 Fig.2 Peak to peak of relative shaft vibration of steam turbine

现场运行时，机组频繁出现阵发性的不稳定振动，对设备的安全运行造成严重干扰。根据现场记录，图2所示800余秒的时间段内出现振动不稳、噪声加剧的现象，但图中所示的八路相对轴振信号的峰峰值并未出现明显的振幅变化，仅轴振信号3Y、4X、4Y在约380 s处有微弱增大，而2X和2Y甚至出现振幅减小的趋势，难以对不稳定振动的激励位置和时刻做出准确判断。

图3为3Y相对轴振信号，在800余秒的时间历程中，其变化非常微弱，分别在125 s和625 s取样分析，两段信号除相位存在差异，振幅几乎一致，不能有效反映汽轮机运行状态的变化。图4分别为125 s和625 s之后1.024 s时间段内振动数据所对应的功率谱密度函数。对比图4(a)与图4(b)，振动信号以50 Hz工频为主要振动成分，图4(b)中25Hz的振动幅值较图4(a)有所增大，说明半速成分是引起不稳定振动的主要原因，结合油膜涡动的振动特点，初步判断支撑轴承可能存在半速涡动，但此时该振动成分不够明显，仅从时间信号和功率谱密度难以获得半速涡动的发生时刻与涡动位置，这也体现了功率谱分析的局限性。

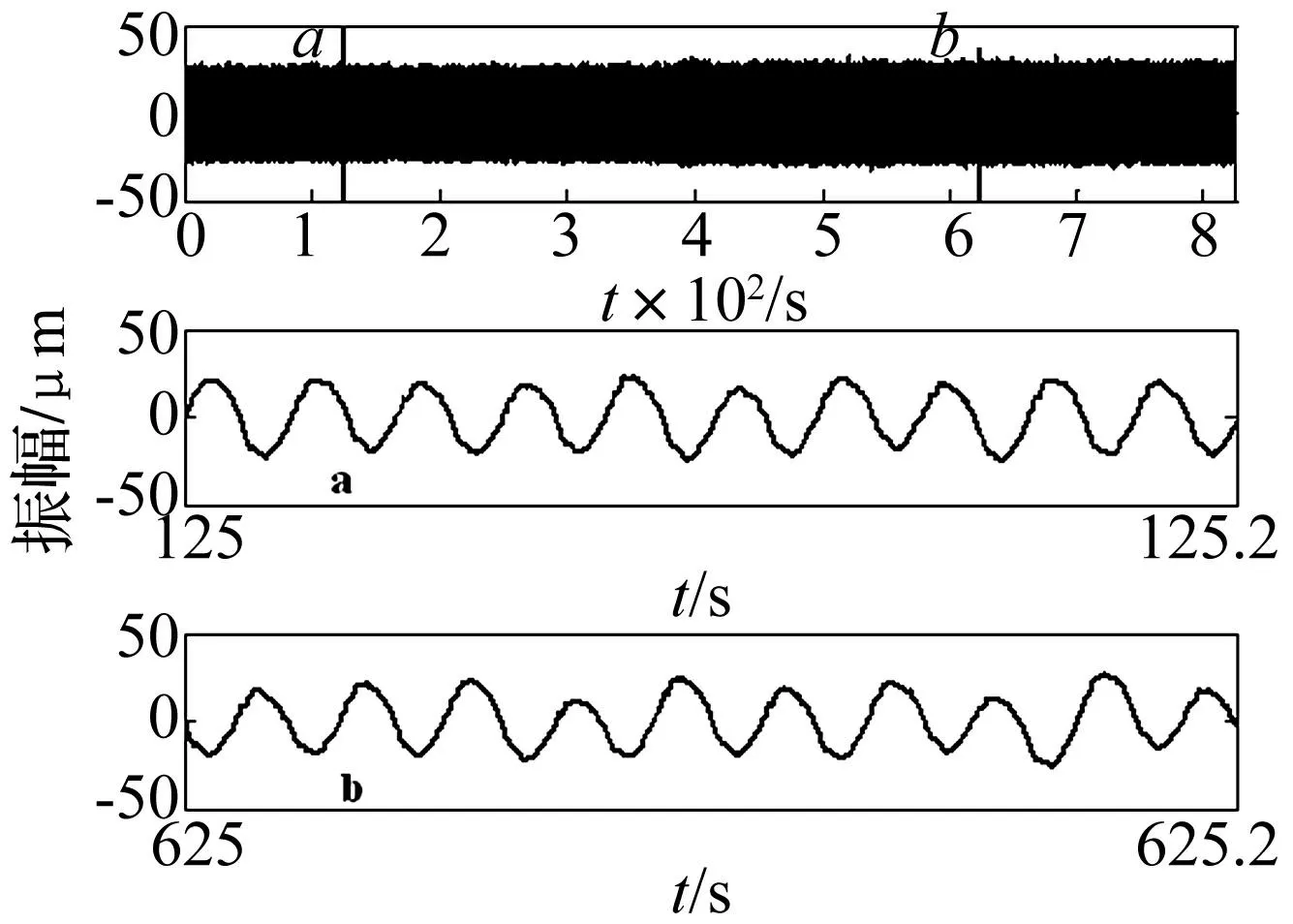
图3　汽轮机3Y轴振信号 Fig.3 Shaft vibration signal of steam turbine in 3Y

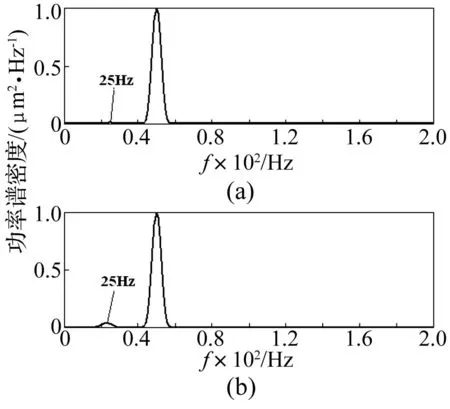
图4　3Y轴振信号的功率谱密度 Fig.4 Power spectrum density of shaft vibration signal of steam turbine in 3Y

基于Gabor变换对3Y轴振信号进行时频分析，为降低运算时间，进行十倍降采样处理，对降采样后的信号进行Gabor变换，时间间隔a=64，频率分段数M=512，其时频分布如图5所示。

图5　3Y轴振信号时频分布 Fig.5 Time frequency distribution of shaft vibration signal in 3Y

由于轴振信号是汽轮机处于工作转速时所测得，且发电负荷基本保持不变(约750 MW)，图5中振动能量以50 Hz及其谐波为主，图4中没有显现的谐波成分(100 Hz、150 Hz等)在图5中有了微弱表现。在约380 s时刻，半速成分(约25 Hz)振动强度明显增加，说明在时域变化不太明显的轴振信号经Gabor时频分析之后出现较为显现的故障特征。为进一步凸显故障特征，将图5中的振动成分进行时频带通滤波，并基于Gabor逆变换予以时域重构，图6为25 Hz、50 Hz和100 Hz振动成分重构后的时间信号，在整个时间历程中，50 Hz和100 Hz的振动幅值保持平稳，而25 Hz的振动幅值在380 s附近产生明显变化，清楚地说明汽轮机的不稳定振动由半速成分(25 Hz)引起。

图6　重构后单频成分振动幅值 Fig.6 Vibration amplitude of single frequency component after reconstruction

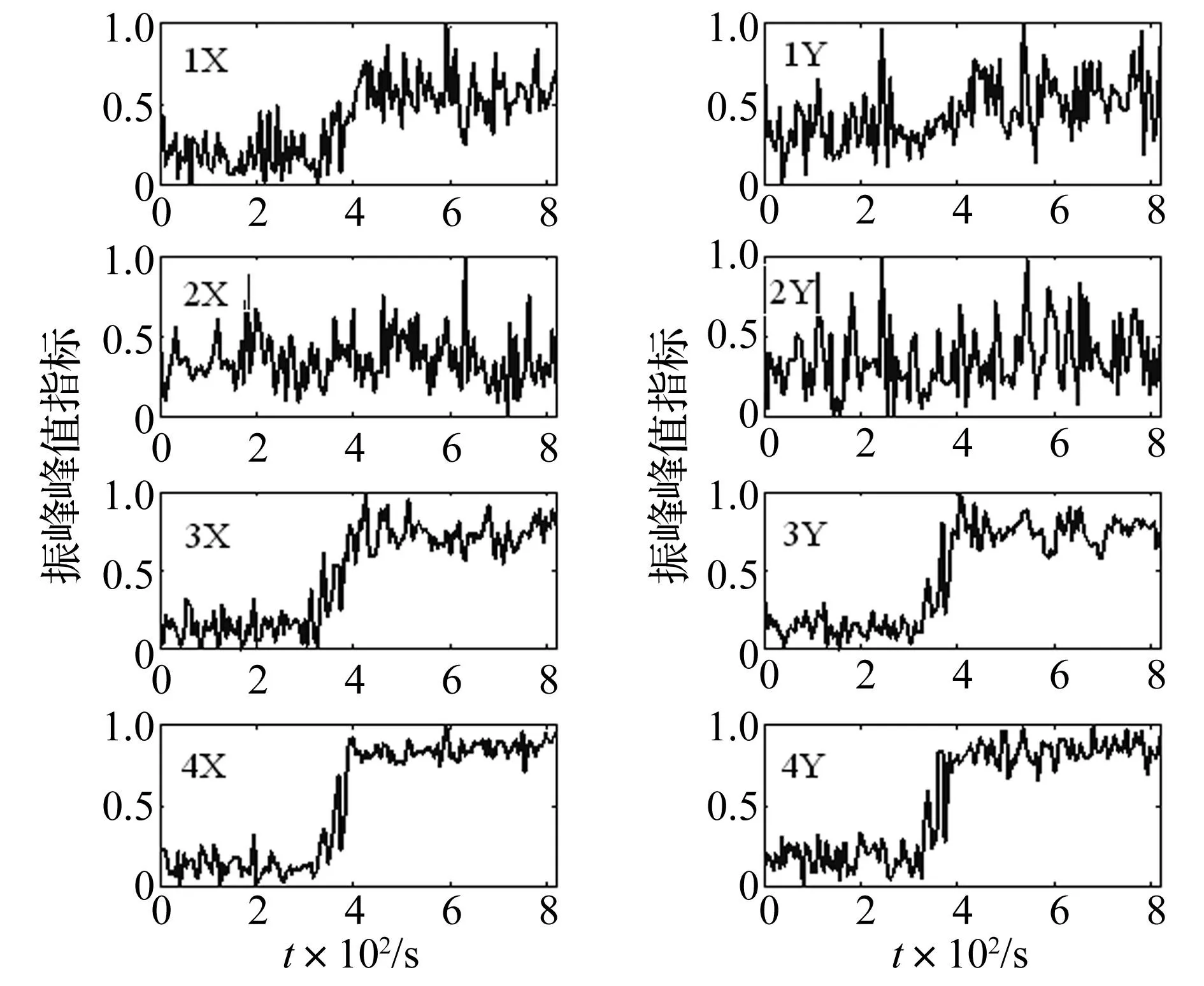
图7　八路轴振信号半速成分峰峰值指标 Fig.7 Peak to peak index of semi-speed component

分别提取八路轴振信号中的半速振动成分，依据式(7)获得的峰峰值指标如图7所示，图7中3X、3Y、4X和4Y的半速成分振动强度在380 s时有明显提升，可作为汽轮机半速涡动的量化特征。1X的半速成分存在微小变化，1Y、2X和2Y对应的半速成分变化不明显。由于不稳定振动发生过程中，汽轮机的发电负荷基本不变，且半速故障特征并未存在于高压缸，可排除半速故障成分由蒸汽激振引起。结合汽轮机的实际结构，判断1号低压缸两端支撑轴承可能存在半速油膜涡动，导致汽轮机阵发性不稳定运行，因此应予以重点排查，并优化支撑轴承结构，及时测量并调节轴承油温。

4结论

滑动轴承的油膜涡动与振荡是导致汽轮机不稳定运行的主要因素。本文基于Gabor变换对850 MW汽轮机轴振信号进行时频变换，获取反映机组不稳定运行的半速成分和发生时刻；进一步在时频平面对半速成分进行带通滤波，并利用Gabor变换的可逆特性，对滤波后的信息予以时间重构，获取汽轮机不稳定运行的量化指标。结果表明，该方法能成功提取汽轮机不稳定运行中的半速特征及发生时刻，并有效进行故障定位，可为汽轮机故障诊断提供依据。

参考文献

[1]姚福生. 汽轮机轴的涡动和油膜振荡[J]. 发电设备，1991, 10: 2-8.

YAO Fu-sheng. Oil whirl and whip of the steem turbine shaft[J]. Power Equipment, 1991,10:2-8.

[2]Jain P C, Srinivasan V. A review of self-excited vibration in oil film journal bearings [J]. Wear, 1975, 31: 219-225.

[3]姚福生. 半速涡动与油膜振荡[J]. 发电设备，1992, 3: 3-9.

YAO Fu-sheng. Semi-speed oil whirl and whip[J]. Power Equipment, 1992,3:3-9.

[4]Muszynska A.Whirl and whip-rotor/bearing stability problems [J]. Journal of Sound and Vibration, 1986, 110(3): 443-462.

[5]杨金福，杨昆，付忠广，等. 滑动轴承轴颈涡动机理的非线性特性研究[J]. 动力工程，2005，25(增): 562-568.

YANG Jin-fu, YANG Kun, FU Zhong-guang, et al. The nonlinear research of sliding bearing journal swirl principal [J].Power Engineering, 2005, 25(s): 562-568.

[6]陈策，杨金福，付忠广. 径向轴承油膜半速涡动及振荡的机理研究[J]. 振动与冲击，2008，27(增)：155-160.

CHEN Ce, YANG Jin-fu, FU Zhong-guang. Research on instability mechanism of oil whirl and oil whip in sliding bearings [J]. Journal of Vibration and Shock, 2008, 27(s): 155-160.

[7]Bachschmid N, Pennacchi P, Vania A. Steam-whirl analysis in a high pressure cylinder of a turbo generator [J]. Mechanical Systems and Signal Processing, 2008, 22(1): 121-132.

[8]刘峻华，黄树红，陆继东. 汽轮机故障诊断技术的发展与展望[J]. 动力工程，2001，21(2):1105-1110.

LIU Jun-hua, HUANG Shu-hong, LU Ji-dong. Development of fault diagnosis for steam turbines [J]. Power Engineering, 2001, 21(2):1105-1110.

[9]孔明. 半速涡动引起的振动故障诊断及处理[C]//第三届安徽自然科学学术年会安徽省电机工程学会论文集，2005，27-30.

[10]朱瑜，张朋波，王雪. 转子系统油膜涡动及油膜振荡故障特征分析[J]. 汽轮机技术，2012，54(4)：306-308.

ZHU Yu, ZHANG Peng-bo, WANG Xue. Fault feature analysis of oil whirl and oil whip for rotor system [J]. Turbine Technology, 2012，54(4)：306-308.

[11]唐贵基，向玲，朱永利. 基于HHT的旋转机械油膜涡动和油膜振荡故障特征分析[J]. 中国电机工程学报，2008，28(2):77-81.

TANG Gui-ji, XIANG Ling, ZHU Yong-li. Fault analysis of oil whirl and oil whip based on Hilbert-Huang transform for rotor system [J]. Proceedings of the Chinese Society for Electrical Engineering, 2008, 28(2):77-81.

[12]胡爱军，朱瑜. 基于阶比分析的转子系统油膜涡动故障诊断研究[J]. 汽轮机技术，2012，54(3)：223-225.

HU Ai-jun, ZHU Yu.Analysis of oil whirl diagnosis based on order analysis for rotor system [J]. Turbine Technology, 2012，54(3)：223-225.

[13]孔庆鹏，宋开臣，陈鹰. 发动机变速阶段振动信号时频分析阶比跟踪研究[J]. 振动工程学报，2005，18(4):448-452.

KONG Qing-peng, SONG Kai-chen, CHEN Ying.Study of time-frequency order tracking of vibration signals in engine speed changing stage [J]. Journal of Vibration Engineering, 2005, 18(4):448-452.

[14]赵晓平，侯荣涛. 基于Viterbi算法的Gabor阶比跟踪技术[J]. 机械工程学报，2009，45(11):247-252.

ZHAO Xiao-ping, HOU Rong-tao. Gabor order tracking based on Viterbi algoithm [J]. Chinese Journal of Mechanical Engineering, 2009, 45(11): 247-252.

[15]金阳，郝志勇，郑旭，等. 基于Gabor重构的发动机振声信号阶次分量瞬时幅值的提取[J]. 振动与冲击，2011，30(9)：15-20.

JIN Yang, HAO Zhi-yong, ZHENG Xu, et al.Extraction of instantaneous amplitude of order components in engine vibroacoustic signals based on Gabor-reconstruction [J]. Journal of Vibration and Shock, 2011, 30(9): 15-20.

[16]申永军，张光明，杨绍普，等. 基于Gabor变换的盲信号分离方法[J]. 振动与冲击，2010，29(10)：166-169.

SHEN Yong-jun, ZHANG Guang-ming, YANG Shao-pu, et al. New method of blind source separation based on Gabor transformation [J]. Journal of Vibration and Shock, 2010, 29(10):166-169.

[17]Bastiaans M J, Geilen M C. On the discrete Gabor transform and the discrete Zak transform [J]. Signal Processing, 1996, 49(3):151-166.

[18]Sondergaard P L. Efficient algorithms for the discrete Gabor transform with a long FIR window [J]. Journal of Fourier Analysis and Application, 2012, 18:456-470.

[19]张贤达. 现代信号处理(第二版) [M]. 北京: 清华大学出版社, 2002.