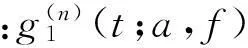广义经验模态分解性能分析与应用
第一作者郑近德男,博士生,1986年生
通信作者程军圣男,博士,教授,博士生导师,1968年生
广义经验模态分解性能分析与应用
郑近德,程军圣,曾鸣,罗颂荣
(湖南大学汽车车身先进设计制造国家重点实验室,长沙410082)
摘要:针对经验模态分解(Empirical Mode Decomposition,EMD)的均值曲线采用三次样条拟合而容易引起包络过冲和不足等缺陷,相关学者提出了许多改进均值曲线的变种EMD方法,取得了一定的效果。广义经验模态分解(Generalized EMD,GEMD)方法综合了多种改进EMD方法,通过定义不同的均值曲线对信号进行逐阶筛分,从得到的每一阶分量中选取最优作为最终的广义内禀模态函数(Generalized Intrinsic Mode Function,GIMF),由于每一阶的GIMF分量都是最优的,因此相较于EMD等单一均值曲线筛分方法,GEMD分解结果也是最优的。论文对GIMF分量准则进行了改进以及对GEMD性能进行了分析,并将GEMD应用于仿真和实测信号的分析,结论表明GEMD分解是完备的和正交的,有比EMD更强的分解能力,而且适合机械振动信号的处理和故障诊断。
关键词:经验模态分解;广义经验模态分解;局部特征尺度分解;分解能力;故障诊断
收稿日期:2013-09-12修改稿收到日期:2014-01-09
中图分类号:TH165+.3; TN911文献标志码:A
基金项目:973项目
基金项目:北京理工大学基础研究基金(20120142009)
Performance analysis and application of generalized empirical mode decomposition
ZHENGJin-de,CHENGJun-sheng,ZENGMing,LUOSong-rong(State key Laboratory of Advanced Design and Manufacture for Vehicle Body, Hunan University, Changsha 410082, China)
Abstract:Aiming at that the mean curve defined in empirical mode decomposition (EMD) fitted with cubic spline may cause envelope overshoot and undershoot, many improved EMDs for improving the mean curve are proposed and some good effects are achieved. Generalized empirical mode decomposition (GEMD) integrates several improved EMD methods and selects the best component from components obtained by sifting different mean curves in each rank as the final generalized IMF (GIMF). Since the GIMF is the best in each rank, the corresponding results of GEMD are also the best. Here, GEMD was introduced firstly and then an improved criterion of GIMF was developed. Furthermore, GEMD was employed to analyze simulated and actual mechanical vibration signals. The results showed that GEMD is complete and orthogonal, it has a better capacity of decomposition than that of EMD, it is suitable for mechanical fault diagnosis as well.
Key words:EMD; GEMD; local characteristic-scale decomposition; capacity of decomposition; fault diagnosis
经验模态分解(Empirical Mode Decomposition,EMD)是由Huang等[1-3]提出的一种自适应的数据处理方法。EMD方法通过定义瞬时频率具有物理意义的内禀模态函数(Intrinsic Mode Function,IMF),同时定义一种基于包络的均值曲线,通过从原始信号中不断分离出包络均值曲线,即执行筛分过程,将原始信号分解为若干个IMF分量和一个剩余项之和。
由于原EMD方法中均值曲线定义为上、下包络线的均值,其中上、下包络线分别由三次样条拟合极大值和极小值而成,因此,不可避免地会产生欠包络和过包络以及拟合误差等问题。Chen等[4]提出了用B样条代替三次样条,以及Peel等[5-6]等提出用有理样条取代三次样条,这两种改进三次样条插值的方法虽然克服了三次样条带来的问题,但同时又引入了其它参数,且由于极值点是固定的,对大部分信号上述两种分解方法的效果不是很明显。盖强和邹岩崑等[7-8]提出的局域波分解方法提出了两种新的均值曲线的定义方法,新的均值曲线避开了上下包络线的定义,直接由数据的极值点定义均值曲线,且只采用一次三次样条拟合,因此节约了计算时间和提高了计算速度。FREI等提出了一种新的时频能分析方法——本征时间尺度分解(Intrinsic Time-scale Decomposition, ITD),ITD基于极值的特征尺度和数据本身线性变换,提高了计算速度,避免了拟合误差以及端点效应向数据内部的扩散影响,然而ITD分解由于采用线性变换,会导致得到的分量出现波形失真。最近,笔者[9]提出了另一种时频分析方法——局部特征尺度分解方法(Local Characteristic-scale Decomposition, LCD),LCD克服了ITD的不足,给出了一种新的均值曲线定义,然而LCD方法本质上也是EMD和ITD的变形方法。
上述改进的EMD方法本质上是对EMD均值曲线的改进,可能对某些信号而言,上述改进的方法在某一方面有一定的提高,而对另外一些信号原EMD方法仍具有其独特的优势;即使对同一个信号不同频段的分量,可能改进的方法提取出的第一个分量较接近实际值,而对于第二个分量则可能是EMD提取的分量更接近实际值。当用上述方法分析实际信号时,无法判定哪种信号处理方法是最合适的和最优的。
基于上述考虑,综合各种改进EMD方法的特点,笔者[10]提出了一种新的时频分析方法——广义经验模态分解(Generalized Empirical Mode Decomposition, GEMD)。GEMD基于不同的均值曲线而定义,从高频到低频进行筛分,从每阶得到的分量中选择最优分量作为最终的广义IMF(Generated IMF,GIMF)。再原始信号中减去该GIMF分量,并将剩余信号视为原始信号,不断重复上述筛分过程,直到剩余信号是一单调或常函数,或者能量与原始信号相比可以忽略的函数。
本文详细研究GEMD方法中GIMF分量的判据准则,在原带宽准则的基础上提出了一种瞬时频率波动能量差准则;同时对GEMD分解的正交性和完备性进行了验证,结果表明GEMD分解是正交的和完备的。最后,以两个正弦信号叠加的混合信号模型为例,对GEMD方法的频率分辨能力进行了研究,结果表明GEMD可分解信号范围要大于EMD,能分解出EMD不能分解的两频率较为接近的信号的叠加信号,是一种具有良好性能的信号分解方法。
1广义经验模态分解
1.1均值曲线的定义
GEMD方法的关键是定义信号合理的均值曲线。然而难点在于,到目前为止,大部分关于均值曲线的定义都是经验性的。综合多种参考文献,论文采用以下六种具有代表性的均值曲线的定义方法:
(1)包络均值曲线(Envelop Mean,EM),定义详见EMD方法[1]。
(2)固有时间尺度均值(Intrinsic Time-scale Mean,ITM)定义参见文献[11]。
(3)局部特征尺度均值(Local Characteristic-scale Mean,LCM),定义参见文献[9]。
(4)极值点中值均值(Extremum- midpoint mean,EMM)。
假设待分析信号为Yt(t≥0),所有极值点为(τk,Yk)(k=1,2,…,M),相邻两个极大值(或极小值)的中点可表示为
(1)
定义
(2)
再用三次样条函数拟合和插值所有的(tk+1,Bk+1)即得到信号Yt的均值曲线。
(5)极值域均值(Extremum Field Mean,EFM),定义参见文献[7]。
(6)局部积分均值(Local Integral Mean,LIM),定义参见文献[12]。

(3)
其中:w(t) 是权重因子。 特别地,二者可定义为:
(4)
上述六种均值曲线的定义方法从不同的角度定义信号的均值曲线,大部分是经验性的,它们的物理模型还有待于进一步验证。
1.2GEMD
设待分析信号为x(t),广义经验模态分解(GEMD)的主要步骤如下[10]。
(1)u0(t)=x(t),j=1;
(2)分别用上述六种方法提取信号uj-1(t)均值曲线:m1(t),m2(t), …,m6(t);
(3)将上述均值曲线mi(t)从uj-1(t)中分离出,得到剩余信号ri(t),即
ri(t)=uj-1(t)-mi(t)(i=1, 2, … 6)
(5)
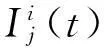
uj(t)=uj-1(t)-Ij(t)
(6)
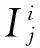
(6)j=j+1,重复上述步骤(2)~(5),直到剩余分量un(t)为一常函数,或单调函数或能量与u0(t)相比可以忽略的函数,停止上述过程。
原始信号x(t)可重写为
(7)
GEMD方法综合了EMD,ITD和LCD等这类分解方法的优势,继承了EMD的筛分过程,通过逐层选优,选出GIMF分量,再对剩余信号重复筛分。与EMD等单一的筛分过程相比,GEMD得到的分量在每一层的分量中是最优的,因此,理论上GEMD分解的结果也是最优的。
1.3GIMF判据
GEMD的原文献采用频率带宽最小来选择GIMF分量。频率带宽反映瞬时频率的调制和波动,频率带宽越小,表明瞬时频率受调制越小,波动越小。
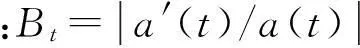
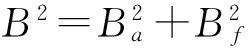
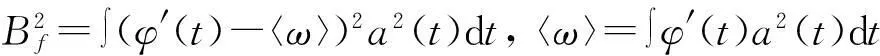
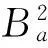
当瞬时频率为常函数时,带宽准则能够很好反映瞬时频率的聚集性。若φ(t)为非常函数时,带宽准则失去了预期的结果。此时,采取如下方案来选择GIMF:

(4)第i个pre-GIMF作为最终的GIMF。

原GIMF判据中通过带宽准则选择GIMF,而改进后的判据弥补了带宽准则的不足,从不同的IMF分量中选择瞬时频率更精确,带宽更小的分量作为最优,相邻的GIMF分量带宽无重叠或者重叠更小,因此分解正交性更好。
此外,由于GEMD是从每层不同的IMF分量中选择最优,如果EMD能将待分解信号分解出,则GEMD也一定能分解出;如果EMD不能分解出,而其它方法定义的均值曲线,如LCM或LIM可以分解出,则说明GEMD也能分解出;只有所有的均值定义方法不能分解出时,GEMD才不能分解出,因此,GEMD的分解能力要比EMD强。
2仿真分析
考虑仿真信号
si(t)=x0(t)+xi(t), i=1,2。 x0(t)=
[1+0.2cos(2π2t)]cos(2πf0t+2πf0/10t2),
x1(t)=cos(2πa1f0t),
x2(t)=cos(2πa2f0t),t∈[0, 1]
(8)
si(t)由调幅调频信号x0(t)和余弦信号叠加而成,其中:f0=30,a1=0.5,a2=0.7。为比较,分别采用EMD和GEMD对s1(t)和s2(t)进行分解,分解结果分别如图1~2和图4~5所示。

C i表示EMD分解得到的第i个IMF分量, res表示剩余项,下同。 图1 混合信号s 1(t)的EMD分解结果 Fig.1 The EMD results of mixed signal s 1(t)

G i表示GEMD分解得到的 第i个GIMF分量,res表示剩余项,下同。 图2 混合信号s 1(t)的GEMD分解结果 Fig.2 The GEMD results of mixed signal s 1(t)
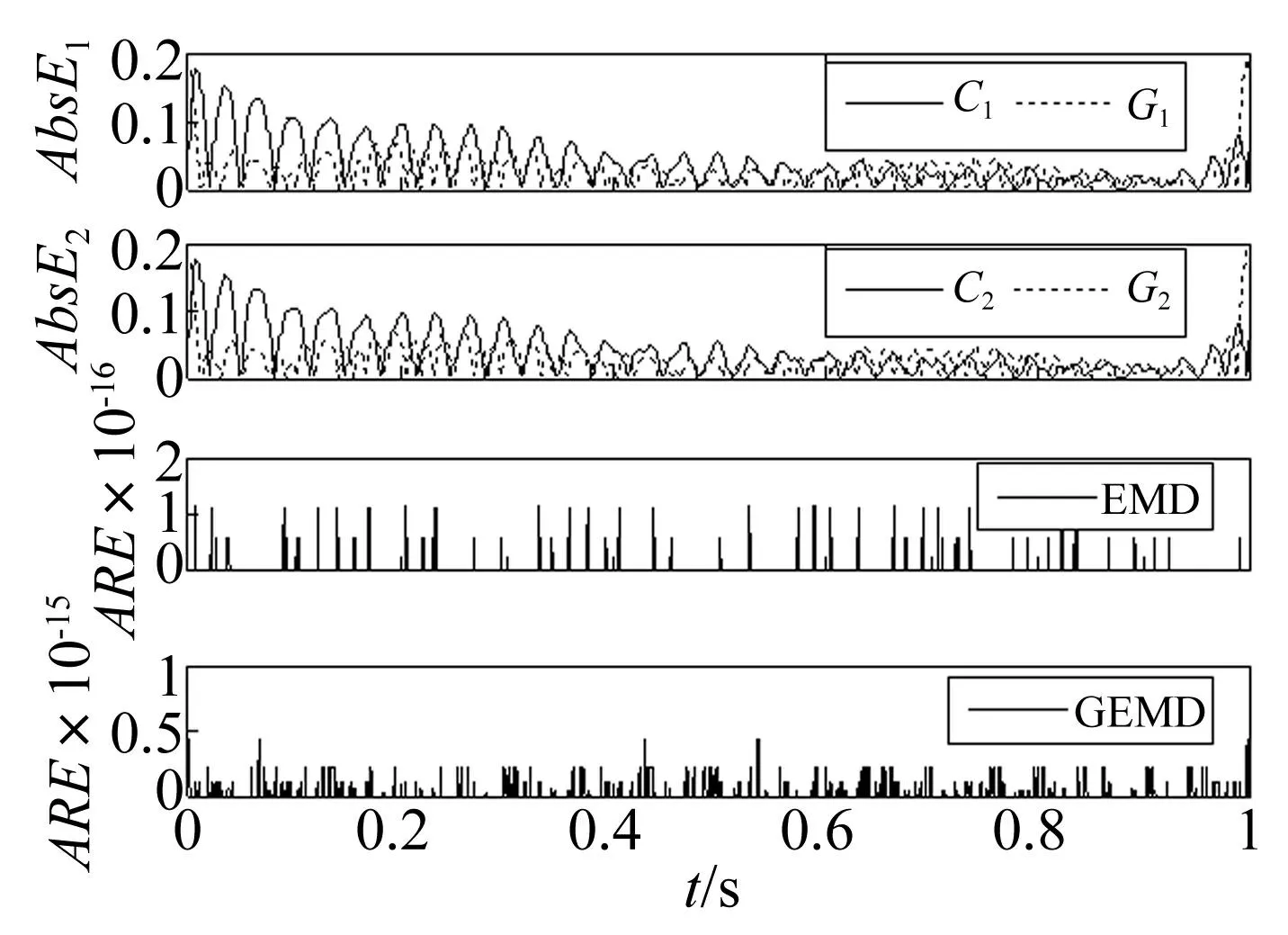
从上到下依次为:第一个和第二个分量与真实分量的绝对误差(实线表示EMD分解结果的绝对误差,虚线表示GEMD分解结果的绝对误差)、EMD分解的重构误差、GEMD分解的重构误差。 图3 混合信号s 1(t)的EMD和 GEMD分解分量的绝对误差和重构误差 Fig.3 The absolute error and reconstruction error of mixed signal s 1(t) generated by EMD and GEMD

图4 混合信号s 2(t)的EMD分解结果 Fig.4 The EMD results of mixed signal s 2(t)

图5 混合信号s 2(t)的GEMD分解结果 Fig.5. The GEMD results of mixed signal s 2(t)
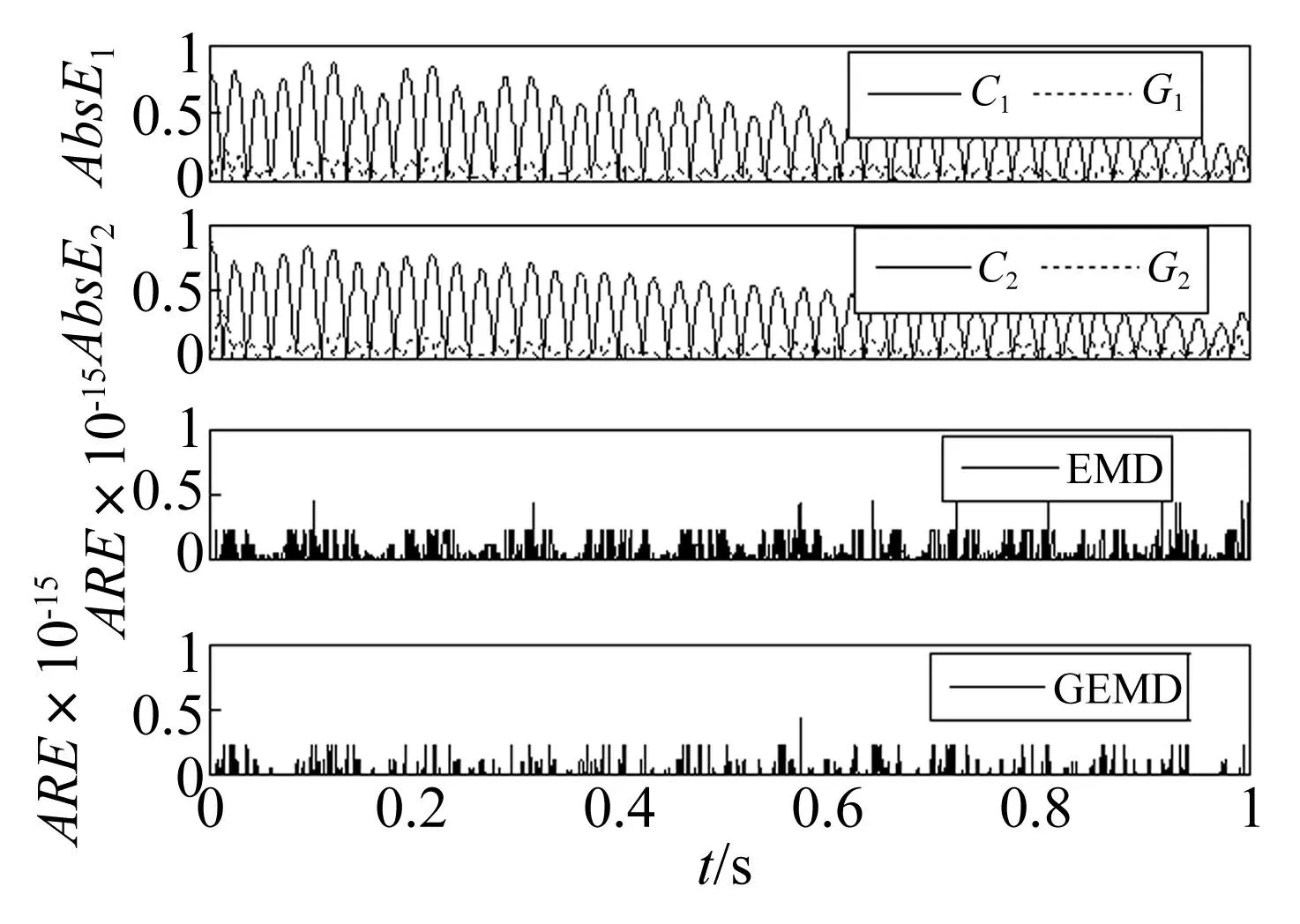
从上到下依次为:第一个和第二个分量与对应真实分量的绝对误差,EMD分解的重构误差,GEMD分解的重构误差。 图6 混合信号s 2(t)的EMD 和GEMD分解分量的绝对误差和重构误差 Fig.6 The absolute error and reconstruction error of mixed signal s 2(t) generated by EMD and GEMD

分析图1至图6可得到以下结论。首先,由图1和图2看出,由于两个分量成分的瞬时频率(30+6tHz,15 Hz)相差较大,EMD和GEMD都能将二者完全分开,且与真实分量绝对误差较小(图3第1, 2行),但GEMD分解效果更好,GIMF分量与真实分量的绝对误差幅值在大部分时间上要小于IMF分量与真实分量的绝对误差幅值。其次,由图4和图5可以看出,由于两个分量成分的瞬时频率(30+6tHz,21 Hz)较为接近,EMD已不能将二者完全分开,分解结果与真实分量相差较大,而GEMD则能够将二者完全分开,与真实分量的绝对误差较小(图6第1, 2行)。再次,由图3和图6也可以看出,对于两个混合信号,EMD和GEMD分解都是完备的,绝对重构误差数量级在10-15。
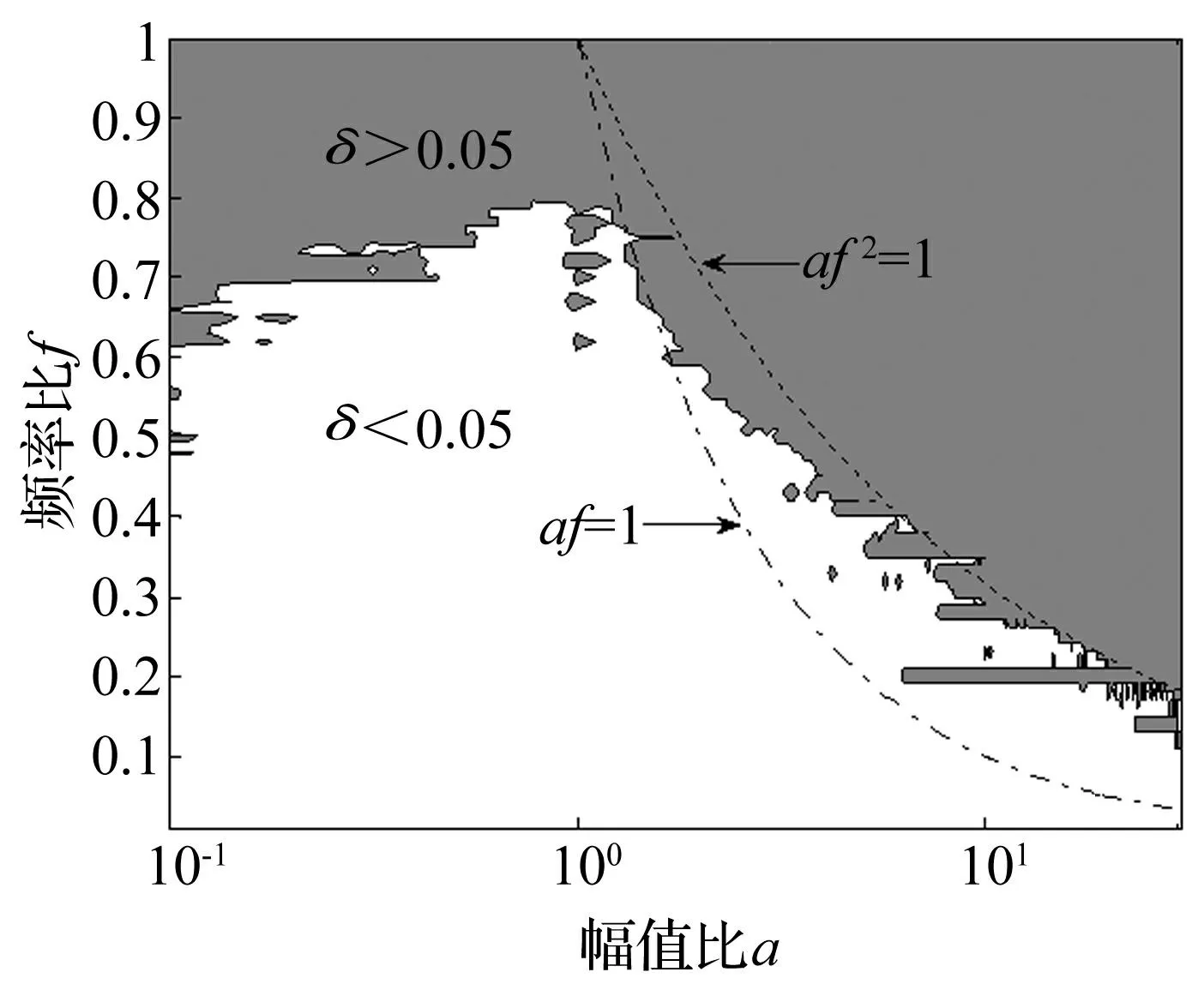
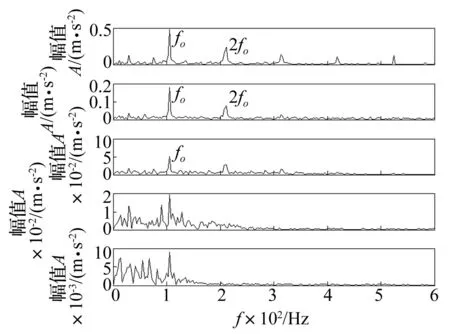
3GEMD分解能力分析
文献[17]以简化的两个正弦信号的叠加模型,对EMD方法的分解能力进行了详细的研究。为了对比分析,仍考虑两个正弦信号叠加模型:
x(t)=cos2πt+acos(2πft+φ)
(9)
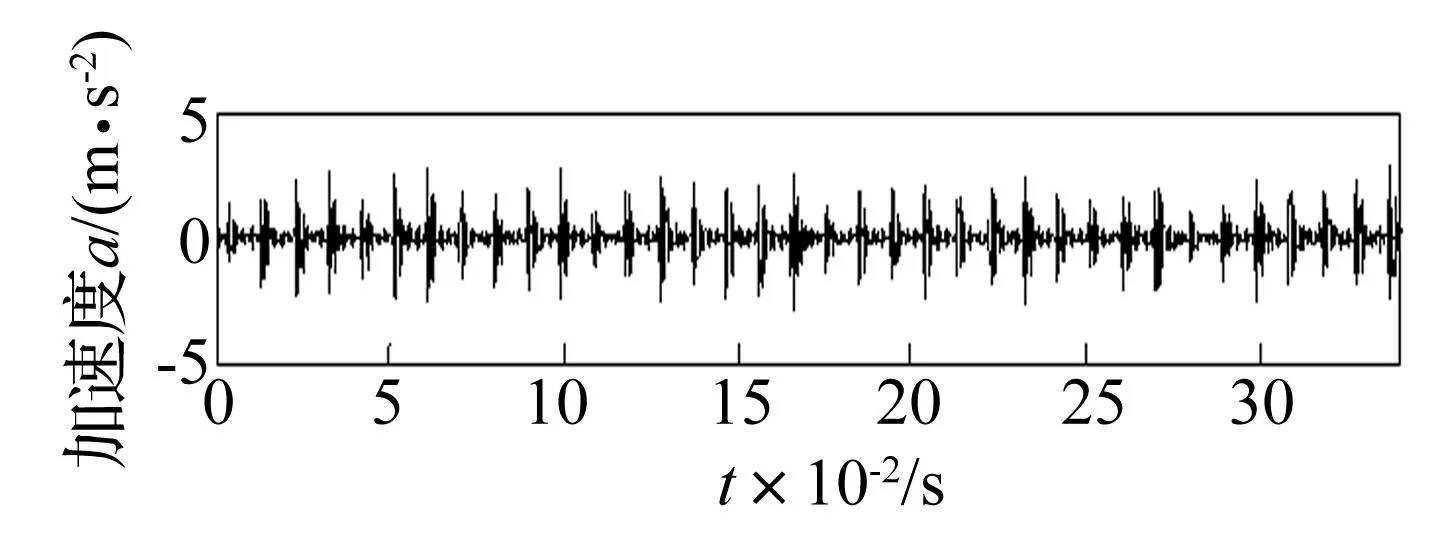
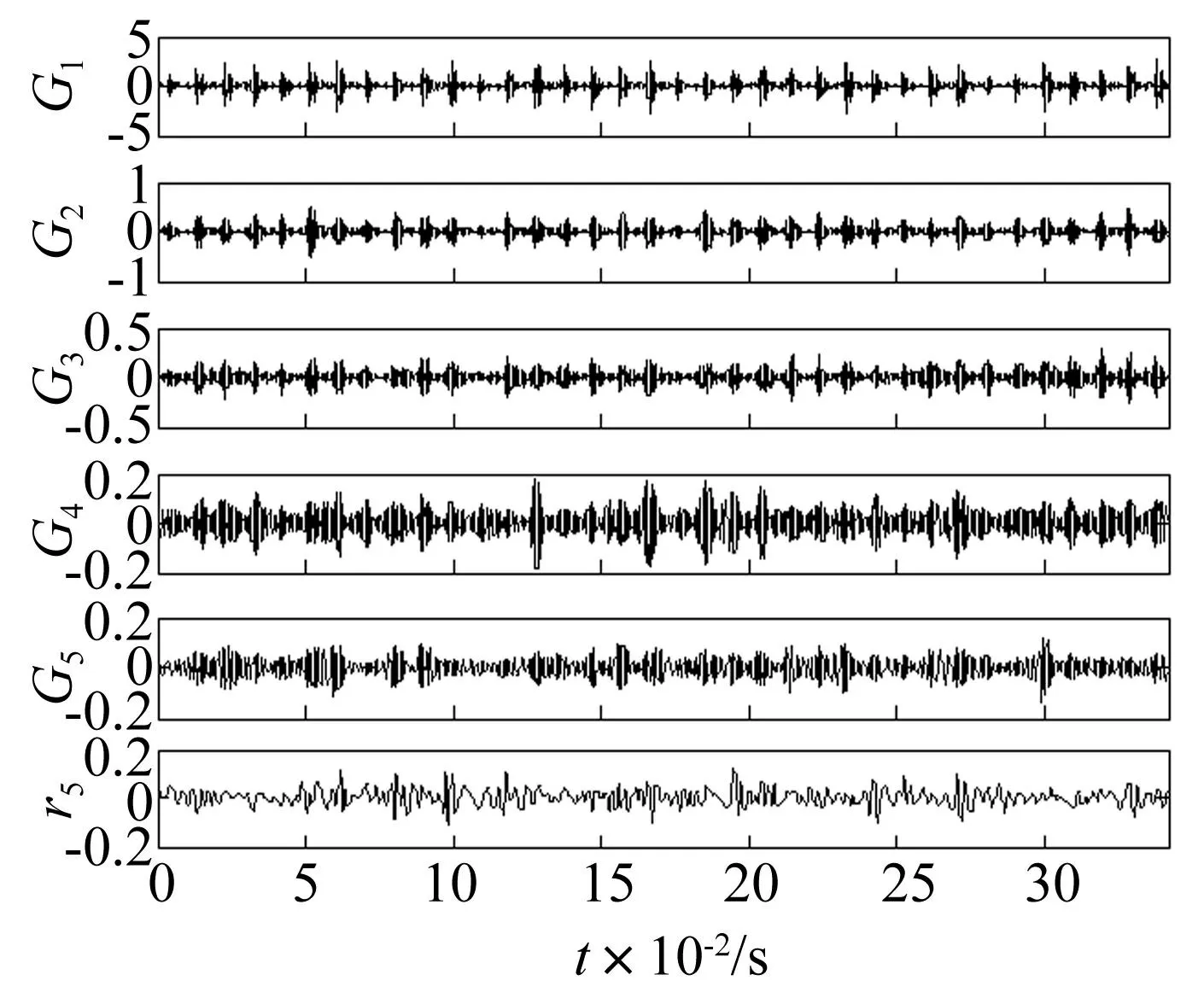
其中:φ表示两信号的初相位差,a表示两信号幅值比,f(0 定义评价指标 δ(a,f)= (10) 图7 两个谐波叠加模型的EMD的分解能力图 Fig.7 The capacity of EMD decomposition of two harmonic superposition model EMD和GEMD的分解能力分别如图7和图8所示。需要说明的是,图7中EMD可分解的分界频率(设为fc)与文献[17]有所差异,这主要是因为采样频率fs以及fs与最大频率fmax的关系对分解效果的影响[19-20]。由图7和图8可以发现,在相同的采样频率和最大频率,相同的最大迭代次数(8次)等条件下,GEMD的分解能力范围要明显大于EMD的分解能力范围。在幅值比a≥1时,曲线af2=1可视为不可分解部分的下边界,af=1可视为可分解部分的上边界。但在二者曲线之间的部分,GEMD的可分解部分仍大于EMD的可分解部分。此外,在幅值比0.1a1时,GEMD能分别出频率更接近的信号。更详细地,①当0.1≤a<0.2时,GEMD可分解边界频率fc≈0.6;EMD可分解边界频率fc≈0.4;②当0.2≤a<0.6时,GEMD可分解边界频率fc≈0.7;而EMD可分解边界频率fc≈0.5;③当0.6≤a≤1时,GEMD的可分解边界频率fc≈0.77. 而EMD可分解边界频率fc≈0.55。 图8 两个谐波叠加模型的GEMD的分解能力图 Fig.8 The capacity of GEMD decomposition of two harmonic superposition model 4应用分析 为了说明GEMD的有效性和相对于EMD的优越性,论文将其应用于具有故障的机械振动信号分析。实验数据采用美国凯撒西储大学公开的轴承数据[21],采用电火花技术对6205-2RS JEM SKF型深沟球轴承设置大小为0.017 78 cm,深度0.027 94 cm的单点故障;在转速为1 750 r/min,负载为0 HP,采样频率为12 kHz的条件下,采集振动加速度信号。不失一般性,以外圈故障轴承的振动加速度信号为例,经计算,转频:fr≈29.2 Hz,外圈故障特征频率:fo≈104.6 Hz。振动信号时域波形如图9所示。 图9 具有外圈故障的轴承振动加速度信号 Fig.9 Vibrationacceleration signal of rolling bearing with out race fault 采用GEMD对其进行分解,结果如图10所示。为了比较和识别故障频率,图11画出了前五个GIMF的包络谱。由图11可以看出,前四个高频分量被故障特征频率调制,第五个分量被故障特征频率和转频调制,解调后的包络谱很明显地反映了外圈故障特征,与实际相符。 其中:G i表示第i个GIMF,图中只画出了前五个GIMF及剩余项 图10 图9所示信号的GEMD分解结果 Fig.10 The results of signal shown in fig.9 decomposed by GEMD; G istands for the ith GIMF and only the first five GIMFs and its residue are shown. 图11 从上到下依次为前五个GIMF的包络谱 Fig.11 Envelope spectrum of the first five GIMFs 其中:c i表示第i个IMF,图中只画出了前五个IMF及剩余项 图12 图9所示信号的EMD分解结果 Fig.12 The results of signal shown in fig.9 decomposed by EMD; c i stands for the ith IMF and only the first five IMFs and its residue are shown 图13 从上到下依次为前五个IMF的包络谱 Fig.13 Envelope spectrum of the first five IMFs 采用EMD对图9所示的信号进行分解,结果如图12所示,为了与GEMD结果比较,其前五个分量的包络谱如图13所示。由图中可以看出,前三个IMF的包络谱与前三个GIMF的包络谱非常接近,从中也可以识别故障,而第四和第五个IMF的包络谱包含的信息则不明显,故障特征频率和转频被低频干扰较严重。因此,比较而言,GEMD分解有一定的优越性。 5结论 对最新提出的广义经验模态分解(GEMD)方法的完备性和正交性进行了数值验证,依据GEMD按照频率从高频到低频的分解特征,提出了一种基于瞬时频率能量波动差的GIMF分量最优评价准则,并对其分解能力进行了详细研究。得出如下结论: (1)GEMD与EMD方法筛分流程相似,分解是完备的和正交的,但GEMD有比EMD更好的正交性。 (2)与EMD相比,GEMD分解能力更强,可分解信号的范围更广。 (3)将GEMD应用于机械故障振动信号的分析,结果表明GEMD不仅适合于机械振动信号的分析,而且有比EMD更好的故障诊断效果。 综上,GEMD是一种有效的信号分解方法。当然,GEMD也有其不足之处,如GIMF分量的评价准则直接决定了分解的效果,而最优GIMF选取准则还有待于进一步研究。相信随着研究的深入和理论的完善,GEMD将会是一种优秀的非线性和非平稳信号处理方法。 参考文献 [1]Huang N E, Zheng S, Long S R,et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc. Roy. Soc. London, 1998, 454: 903-995. [2]Wu Z, Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[J].Proc. R. Soc. London A, 2004, 460: 1597-1611. [3]Hou T Y, Yan M P, Wu Z. A variant of the EMD method for multi-scale data, Adv. Adapt. Data Anal.1,2009:483-516. (下转第155页) N E, Zheng S, Long S R,et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc. Roy. Soc. London, 1998, 454: 903-995. [2]Wu Z, Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[J].Proc. R. Soc. London A, 2004, 460: 1597-1611. [3]Hou T Y, Yan M P, Wu Z. A variant of the EMD method for multi-scale data, Adv. Adapt. Data Anal.1,2009:483-516. [4]Chen Qiu-hui, Huang Norden, Riemenschneider Sherman, et al. A B-spline approach for empirical mode decompositions[J].Advances in Computational Mathematics, 2006, 24: 171-195. [5]Peel M C, McMahon T A, Pegram G G S. Assessing the performance of rational spline-based empirical mode decomposition using a global annual precipitation dataset[J]. Proc. R. Soc. A, 2009, 465: 1919-1937. [6]Pegram G G S, Peel M C,McMahon T A. Empirical mode decomposition using rational splines: an application to rainfall time series[J]. Proc. R. Soc. A., 2008, 464:1483-1501. [7]盖强. 局域波时频分析方法的理论研究与应用[D]. 大连:大连理工大学, 2001. [8]邹岩崑. 局域波分析的理论方法研究及应用[D]. 大连:大连理工大学, 2004. [9]程军圣,郑近德,杨宇. 一种新的非平稳信号分析方法—局部特征尺度分解法[J].振动工程学报,2012, 25(2): 215-220. CHENG Jun-sheng, ZHENG Jin-de, YANG Yu.A new nonstationary signal analysis approach-the local characteristic-scale decomposition method[J]. Journal of Vibration Engineering, 2012, 25(2):215-220. [10]Zheng Jin-de, Cheng Jun-sheng, Yang Yu. Generalized empirical mode decomposition and its applications to rolling element bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2013, 40(1):136-153. [11]Frei M G,Osorio I.Intrinsic time-scale decomposition:Time-frequency-energy analysis and real-time filtering of non-stationary signals[J].Proc. Royal Soc. A, 2007, 463:321-342. [12]Hong Hong, Wang Xin-long, Tao Zhi-yong. Local integral mean-based sifting for empirical mode decomposition[J]. IEEE signal processing letters, 2009, 16(10): 841-844. [13]Cohen L. Time frequency analysis: theory and applications [M]. Prentice Hall Press, 1995. [14]Xuan B, Xie Q, Peng S.EMD sifting basedon band width [J]. IEEE Signal Process. Lett, 2007,14(8):537-540. [15]郑近德,程军圣,杨宇. 一种新的估计瞬时频率的方法—经验包络法[J].振动与冲击,2012, 31 (17): 86-90. ZHENG Jin-de, YANG Yu, CHENG Jun-sheng,A new instantaneous frequency estimation approach-empirical envelope method[J].Journal of Vibration and Shock, 2012, 31 (17): 86-90. [16]Huang N E, Wu Z H, Long S R, et al. On the frequency [J]. Advances in Adaptive Data Analysis, 2009, 1(2): 177-229. [17]Rilling G,Flandrin P. One or two frequencies the empirical mode decomposition answers[J]. IEEE Trans. Signal Process., 2008, 56(1): 85-95. [18]杨宇,曾鸣,程军圣.局部特征尺度分解方法及其分解能力研究[J].振动工程学报,2012, 25(5):602-609. YANG Yu, ZENG Ming, CHENG Jun-sheng.Research on local characteristic-scale decomposition and its capacities[J].Journal of Vibration Engineering, 2012, 25(5):602-609. [19]Rilling G, Flandrin P. On the influence of sampling on the empirical mode decomposition[J]. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2006:444-447. [20]Rilling G, Flandrin P. Sampling effects on the empirical mode decomposition [J]. Advances in Adaptive Data Analysis,2009, 1(1): 43-59. [21]Xu H B, Chen G H, An intelligent fault identification method of rolling bearings based on LSSVM optimized by improved PSO[J]. Mechanical Systems and Signal Processing,2013,35:167-175. Qiu-hui, Huang Norden, Riemenschneider Sherman, et al. A B-spline approach for empirical mode decompositions[J].Advances in Computational Mathematics, 2006, 24: 171-195. [5]Peel M C, McMahon T A, Pegram G G S. Assessing the performance of rational spline-based empirical mode decomposition using a global annual precipitation dataset[J]. Proc. R. Soc. A, 2009, 465: 1919-1937. [6]Pegram G G S, Peel M C,McMahon T A. Empirical mode decomposition using rational splines: an application to rainfall time series[J]. Proc. R. Soc. A., 2008, 464:1483-1501. [7]盖强. 局域波时频分析方法的理论研究与应用[D]. 大连:大连理工大学, 2001. [8]邹岩崑. 局域波分析的理论方法研究及应用[D]. 大连:大连理工大学, 2004. [9]程军圣,郑近德,杨宇. 一种新的非平稳信号分析方法—局部特征尺度分解法[J].振动工程学报,2012, 25(2): 215-220. CHENG Jun-sheng, ZHENG Jin-de, YANG Yu.A new nonstationary signal analysis approach-the local characteristic-scale decomposition method[J]. Journal of Vibration Engineering, 2012, 25(2):215-220. [10]Zheng Jin-de, Cheng Jun-sheng, Yang Yu. Generalized empirical mode decomposition and its applications to rolling element bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2013, 40(1):136-153. [11]Frei M G,Osorio I.Intrinsic time-scale decomposition:Time-frequency-energy analysis and real-time filtering of non-stationary signals[J].Proc. Royal Soc. A, 2007, 463:321-342. [12]Hong Hong, Wang Xin-long, Tao Zhi-yong. Local integral mean-based sifting for empirical mode decomposition[J]. IEEE signal processing letters, 2009, 16(10): 841-844. [13]Cohen L. Time frequency analysis: theory and applications [M]. Prentice Hall Press, 1995. [14]Xuan B, Xie Q, Peng S.EMD sifting basedon band width [J]. IEEE Signal Process. Lett, 2007,14(8):537-540. [15]郑近德,程军圣,杨宇. 一种新的估计瞬时频率的方法—经验包络法[J].振动与冲击,2012, 31 (17): 86-90. ZHENG Jin-de, YANG Yu, CHENG Jun-sheng,A new instantaneous frequency estimation approach-empirical envelope method[J].Journal of Vibration and Shock, 2012, 31 (17): 86-90. [16]Huang N E, Wu Z H, Long S R, et al. On the frequency [J]. Advances in Adaptive Data Analysis, 2009, 1(2): 177-229. [17]Rilling G,Flandrin P. One or two frequencies the empirical mode decomposition answers[J]. IEEE Trans. Signal Process., 2008, 56(1): 85-95. [18]杨宇,曾鸣,程军圣.局部特征尺度分解方法及其分解能力研究[J].振动工程学报,2012, 25(5):602-609. YANG Yu, ZENG Ming, CHENG Jun-sheng.Research on local characteristic-scale decomposition and its capacities[J].Journal of Vibration Engineering, 2012, 25(5):602-609. [19]Rilling G, Flandrin P. On the influence of sampling on the empirical mode decomposition[J]. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2006:444-447. [20]Rilling G, Flandrin P. Sampling effects on the empirical mode decomposition [J]. Advances in Adaptive Data Analysis,2009, 1(1): 43-59. [21]Xu H B, Chen G H, An intelligent fault identification method of rolling bearings based on LSSVM optimized by improved PSO[J]. Mechanical Systems and Signal Processing,2013,35:167-175.