基于联合采用EMD与高通低通滤波的信号分析

李光耀　马新斐　郭盼盼　杨波

【摘 要】提出一种基于Hilbert-黄变换改进的信号分析方法。实验表明经验模态分解（EMD）方法在大多数情况下分解的结果都与人们的直观感觉相符合。但实验也发现，常规的EMD分解方法无法将频率存在2倍关系内的信号分量分离而可能导致分量模态混叠。为解决模态混叠问题，我们先将原始信号通过高通低通滤波分为两组。之后，再对两组信号分别进行经验模态分解，并进行频谱分析。经过实验验证，使用该方法可以有效地将存在二倍频率内的信号分离开来，达到消除本征模态函数（IMF）的混叠的效果。

【关键词】模态函数；滤波；经验模态分解

【Abstract】An improved method based on Hilbert Huang transform is proposed to analysis signal. The experiments show that decomposition results used the method of the empirical mode decomposition（EMD） are consistent with peoples intuitive sense in most cases. But the test also found that， the signal components within the same octave can not be separated through it. In order to solve the problem of mode mixing， original signal is divided into two groups through a high-pass and low-pass filter firstly. After that， two groups are analyzed by using empirical mode decomposition， and the spectrum of signal component is further analyzed one by one. The experiments prove that the signal components within the same octave can be divided effectively through this method to eliminate the aliasing of the intrinsic mode function（IMF）.

【Key words】Mode function； Filtering； Empirical mode decomposition

0 引言

Huang于1998年提出了一种新的非线性信号分解方法希尔伯特-黄变换（Hilbert-Huang Transform，简称HHT）[2]。它包括两个步骤：①通过经验模态分解（Empirical Mode Decomposition，简称EMD）将信号分解成有限个本征模态函数（Intrinsic Mode Function 简称IMF）；②对IMF进行Hilbert变换从而得到瞬时频率和瞬时幅值。HHT从根本上脱离了传统的傅里叶变换的束缚，且不存在基函数选择的缺陷，能够依据信号灯局部时变特征进行自适应的时频分解，得到信号的瞬时频率，从而真实地描述信号的物理特征，且在心电信号预处理问题上取得了较好的效果。但是，实际应用时EMD存在的模态混叠问题还是不能避免，即当信号中的两个组成分量的频率在2倍频内时，EMD无法将其分解开。而联合使用高通低通滤波能够一定程度上解决EMD无法对2倍频内信号分解的问题，从而对信号进行更彻底的滤波，结果分析也佐证了联合消噪法的有效性。

1 HHT信号分析方法简介

用HHT在对信号的处理和分析上，过程分为两个部分，即经验模态分解与希尔伯特变换。原始信号经EMD分解后变换为多个固有模态函数（IMF）与一个残余项之和，接着对IMF进行希尔伯特变换，对其做瞬时频率及振幅分析。EMD分解后的每个固有模态函数与残余项分别对应某一频带中的信号成分，根据噪声所处的频带范围可以适当去除或者抑制，从而实现消噪的目的。

1.1 经验模态分解（EMD）

EMD方法假设任何信号都由不同的本征模态函数构成，每个IMF分量可以是非线性的，也可以是线性的。IMF分量需要满足下面两个条件：①极值点个数和过零点个数相等或者至多相差1；②在任意时刻，局部的上下包络关于时间轴是对称的。

这样原始信号就能够被分解成有限个不同频率的模态函数。其分解过程也有条件，即：①极大值和极小值必定有一对；②极值间隔可以决定其时域特性；③如果数据序列完全缺乏极值但是仅仅包含拐点，那么它也可以通过求导一次或者多次来找到极值点。

具体分解过程可以理解为一个筛选的过程。筛选过程如下：

2 EMD与高通低通滤波的联合使用

2.1 二倍频内信号定义

假设源信号s（t）是由已知的三种信号分量a，b和c组成的混合信号，且三种信号的频率分别为fa，fb，fc。经过实验验证，当任意两个信号的频率之比如：fc / fb<2，时，采用EMD时会发生模态混叠，即不能将源信号s（t）分解为已知的信号分量。那么在这里，定义信号c，b是二倍频内信号。

2.2 验证二倍频内信号的混叠

为验证所提到的二倍频内信号会发生模态混叠的假设，本节给出例子来证明。假设有原始信号：

s（t）=3cos（2？仔50t）+6cos（2？仔100t）+5sin（2？仔150t）+10sin（2？仔350t）

设置采样频率为2000Hz，采集0.5s的数据，即1000点数据。原始信号s（t）及其频谱图如图1。

利用常规EMD方法对原始信号s（t）进行分解，得到各IMF分量，各个IMF分量如图2所示（横坐标为数据点数）。

由上图直观判断可知：采用常规的EMD方法分解原始信号后，imf2分量存在混叠。将分量信号进行频谱分析，各个IMF分量的频谱图如图3所示（横坐标为：频率/Hz）。

由上图可知，信号分量imf2确实存在信号的混叠，混叠的信号频率为100Hz和150Hz，且150/100<2。二倍频内信号混叠得以验证。

2.3 基于高通低通滤波的EMD

由于直接对原始信号用EMD方法分解无法分离二倍频内信号。可以首先对原始信号进行频谱分析确定信号中的组成成分，之后通过高通低通滤波将频率在2倍内条件的信号分别分成两组，最后采用EMD方法分别对分离开来的信号进行分解。

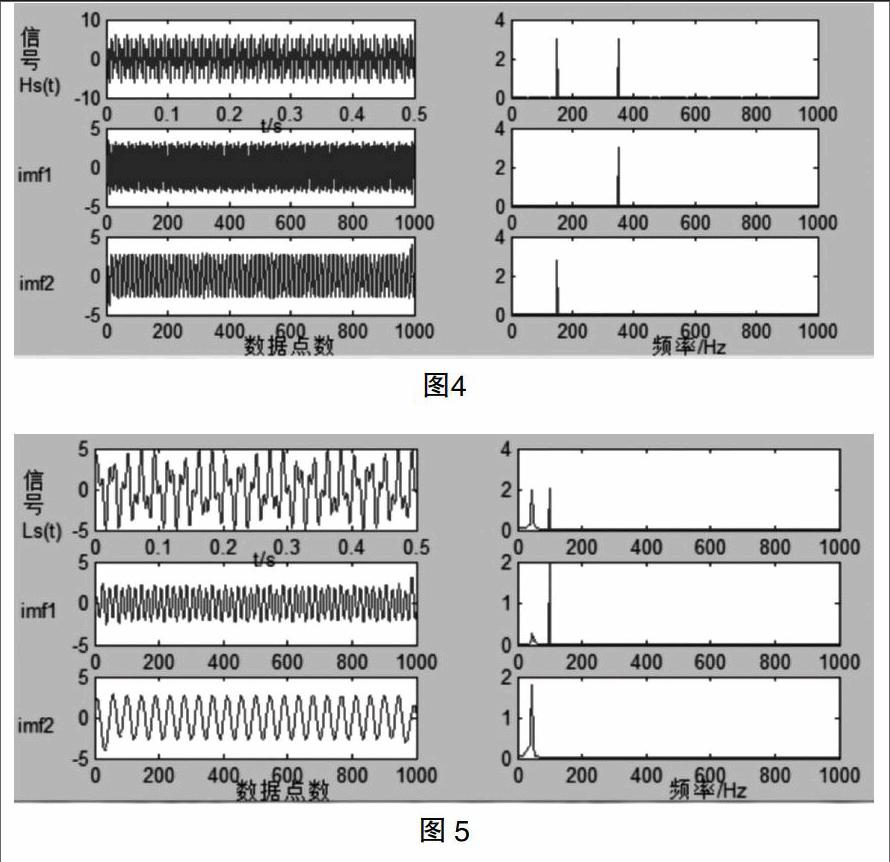
假设给定任意一个原始信号s（t）（在此假设s（t）仍然为上文中的原始信号，但未知信号组成），由上文中对s（t）进行频谱分析可知，原始信号s（t）中含有EMD分解后将要混叠的子信号，即100Hz和150Hz的两个信号。然后用低通滤波器将低于150Hz的信号分离出来定义为Ls（t），用高通滤波器将高于100Hz的信号分离出来点定义为Hs（t）。分别对Ls（t）、Hs（t）进行分析，如下图4、图5所示：

由图4、图5可得，原始信号s（t）经过基于高通低通滤波的EMD后分解为四种频率的子信号：图4中的imf1（350Hz）、imf2（150Hz）和图5中的imf1（100Hz）、imf2（50Hz）。从而可以定量地去除其中某个信号以达到精确滤波的目的。

3 结论

在对Hilbert-黄变换的基本原理进行分析的基础上，发现仅仅采用EMD方法不能够将二倍频内信号分解开来，即不能去除二倍频内信号的的某个信号。之后，通过采用傅里叶变换和高通低通滤波这两种方法，解决了常规EMD方法无法分解二倍频内信号的问题，并给出例子证明其有效性，从而能够定量的去除任意一种频率的信号。

【参考文献】

[1]张喜红，王玉香，杨志清.基于HHT的心电信号滤波算法的研究[J].吉林化工学院学报，2014（1）：51-54.

[2]Huang N E， Shen Z， Long S R ， et al. The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis[J].Proceedings of the Royal society of London Series A，1998，45（4）：903-995.

[3]Huang N E， Shen Z， Long S R. A new view of non-linear water waves：the Hilbert spectrum[J].Annual review of Fluid Mechanics，1999，31（1）：417-457.

[4]郭喜平，王立东，张喜红.经验模态分解（EMD）新算法及应用[J].噪声与振动控制，2008，5（10）：70-72.

[5]傅志方，华宏星.模态分析理论与应用[M].上海：上海交通大学出版社，2000.

[责任编辑：王楠]