基于改进的希尔伯特振动分解的机械故障诊断方法研究
第一作者唐贵基男,教授,1962年生
基于改进的希尔伯特振动分解的机械故障诊断方法研究
唐贵基,庞彬
(华北电力大学机械工程系,河北保定071003)
摘要:针对多分量机械故障振动信号的特征提取问题,介绍一种基于希尔伯特振动分解(HVD)的时频分析方法。该方法首先利用Hilbert变换得到原始振动信号的解析信号,然后通过对解析信号的瞬时频率低通滤波获得信号中幅值最大分量的瞬时频率,同时经同步检测获得相应的瞬时幅值和初相位,最后经过迭代运算自适应地检测出原信号各分量的时频信息。针对HVD方法的边界效应问题,提出一种基于相关系数准则的波形匹配边界延拓法对其进行改进。通过两组仿真信号分析验证了HVD方法对多分量非平稳信号的分解能力,同时表明改进的HVD方法能很好地抑制边界效应。给出转子系统油膜涡动故障诊断实例,验证了该方法的工程实用性。
关键词:希尔伯特振动分解;多分量信号;时频分析;波形匹配延拓;机械故障诊断
收稿日期:2014-01-02修改稿收到日期:2014-02-03
中图分类号:TH133.3;TH17文献标志码:A
A mechanical fault diagnosis method based on improved Hilbert vibration decomposition
TANGGui-ji,PANGBin(School of Mechanical Engineering,North China Electric Power University,Baoding 071003,China)
Abstract:A time-frequency approach based on Hilbert vibration decomposition (HVD) method was introduced in order to extract fault features of multi-component mechanical fault vibration signals accurately. Firstly, the analytical signals of the original vibration signals were obtained through Hilbert transformation. Secondly, the instantaneous stationary frequency of the largest amplitude component was achieved using a low-pass filtering of analytical signals’ instantaneous frequencies, the corresponding amplitude and initial phase were also estimated according to the synchronous detecting, then the time-frequency information of each component of the original signal was detected adaptively with iteration computation. Aiming at the end effects of HVD, a wave matching extending method based on correlation coefficient criteria was proposed to improve HVD. The analysis of two groups of simulated signals showed a good capacity of HVD in decomposing the non-stationary multi-component signals, and the results showed that the improved HVD suppresses its end effects. Finally, a fault diagnosis instance of an oil whirl of a rotor system was given to validate the feasibility of this method.
Key words:Hilbert vibration decomposition; multi-component signal; time-frequency analysis; wave matching extending;mechanical fault diagnosis
机械系统元件发生故障时,振动信号通常为多分量非平稳信号,采用合适的时频分析方法提取振动信号中各个分量的时频分布信息是故障特征提取和故障类别判断的关键[1]。机械故障诊断中常用的时频分析方法有:Wigner-Ville分布、小波分析、希尔伯特黄变换(Hilbert Huang Transform, HHT)等[2-4]。其中:Wigner-Ville分布具有理论上最高的时频凝聚性,但处理多分量信号时存在严重的交叉项干扰问题[5]。小波分析缺乏足够的自适应性,一旦小波基函数选定,那么所有数据都必须用此小波函数分析,易造成信号的能量泄漏,使定量的时频分析变得困难[6]。HHT由EMD和希尔伯特变换两部分组成,方法简单,应用较广。但EMD理论上具有模态混叠、端点效应、过包络、欠包络等缺陷,很大程度上影响了HHT的分析精度[7]。
希尔伯特振动分解是Feldman等[8]在总结上述时频分析方法基础上提出的一种非平稳信号分析的新方法。该方法首先利用Hilbert变换获得原始信号的解析信号,然后通过低通滤波对原信号的非平稳频率成分进行分离,获得信号中幅值最大的分量的瞬时频率,并经同步检测得到该分量的瞬时幅值和初相位,最后通过迭代运算自适应检测出原信号各个分量的时频信息。HVD和HHT方法都以希尔伯特变换为基础,但HVD方法避免了HHT方法中复杂的EMD过程,对多分量非平稳信号进行分析,具有分解精度高,分解速度快的优点。针对HVD的边界效应问题,提出一种基于相关系数准则的波形匹配边界延拓法来对其进行改进。应用该方法对仿真信号和转子系统油膜涡动实验测试信号进行分析,分析结果验证了HVD方法对非平稳信号良好的时频分析效果,通过对比分析表明改进后的HVD方法消除了自身的端点问题,使得分析结果更加精确。
1HVD的基本原理
1.1Hilbert变换
任一非平稳连续时间信号x(t)的Hilbert变换可表示为[9]
(1)
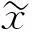
(2)
式中:A(t)和φ(t)分别对应x(t)的瞬时幅值和瞬时相位,表达式分别为
(3)
(4)
对应瞬时频率表达式为
(5)
1.2幅值最大分量的频率估计
多分量非平稳信号x(t)可表示为[10]
(6)
式中:N为x(t)中的分量个数,al(t)、fl(t)、θl、φl(t)分别表示第l个分量的瞬时幅值、瞬时频率、初相位和相位。则经Hilbert变换,x(t)的解析信号为
(7)
参考文献[10],x(t)的瞬时幅值A(t)可表示为
(8)
其中:
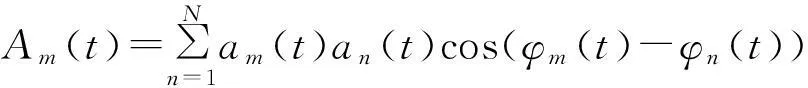
(9)
式中:m=1,2,N
同时x(t)的瞬时频率f(t)可表示为
(10)
上式表明f(t)可表示为两部分,其中第1部分f1(t)为幅值最大分量的瞬时频率,第2部分为相对于f1(t)快速变化的振荡频率部分。因而实际应用中可通过低通滤波滤除f(t)的高频振荡频率,得到幅值最大分量的瞬时频率f1(t)。本文采用FIR低通滤波器,为了实现不同瞬时频率成分的完全分离,截止频率fc需小于相邻次分量瞬时频率差值绝对值的最小值,则fc越小越能实现不同分量的准确检测。通常fc设为采样频率的0.01~0.05倍时即可完全滤除f(t)的高频振荡频率。实际分析中在考虑滤波器稳定性的前提下,若需要设定更小的截止频率,可采用降采样的方法实现。
1.3同步检测求幅值和相位
将以上估计的瞬时频率看作参考频率fr(t),构造两正交信号cos(2π∫fr(t)dt)、sin(2π∫fr(t)dt)。将x(t)与cos(2π∫fr(t)dt)相乘得下面表达式
cos(2π∫(fl=r(t)+fr(t))dt+θl=r))
(11)
同理将x(t)与sin(2π∫fr(t)dt)相乘得
sin(2π∫(fl=r(t)+fr(t))dt+θl=r))
(12)
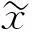
(13)
(14)
从而同步检测得到瞬时频率为fr(t)的分量的瞬时幅值ar(t)和初相位θr为:
(15)
(16)
1.4迭代运算
根据上述步骤提取出x(t)中幅值最大的分量
x1(t)=a1(t)cos(2π∫f1(t)dt+θ1)
(17)
将x(t)与x1(t)的差作为初始信号,即
xN-1=x(t)-x1(t)
(18)
重复1.2和1.3节的步骤获得x2(t)。通过迭代运算依次获得其他分量的时频信息,将式(18)的归一化标准差作为迭代终止条件σ,当σ<0.001时迭代停止。
2基于相关系数准则的波形匹配边界延拓法
HVD算法以Hilbert变换为基础,并且在对各分量的频率、幅值、和相位估计过程中应用到了低通滤波。由于Hilbert变换和低通滤波均存在边界效应,使得当前分量的检测产生误差。并且随着迭代运算的不断累积,误差会越来越大,严重影响了HVD算法的检测精度。目前,解决边界效应的一种有效方法是对信号进行边界延拓[11]。为降低数据延拓的偶然性误差,本文提出一种基于相关系数准则的波形匹配边界延拓新方法。具体步骤如下:
(1)假设样本数量为n的离散信号x(t)为{x(t1),x(t2),x(t3),…,x(tn)},共有m个极大值点和p个极小值点,其中信号采样间隔t=ti-ti-1。极大值点:indmax={M(1),M(2),…,M(m)},对应时间为tmax={tmax1,tmax2,…,tmax m}。极小值点:indmin={N(1),N(2),…,N(p)},对应时间为tmin={tmin1,tmin2,…,tmin p}。
(2)如图1所示,以左边界第一极值点为极大值点为例,选取左端点到第2个极值点间的波形{x(t1) ,…,x(tmax1) ,…,x(tmin1)}为研究对象,记为w1。
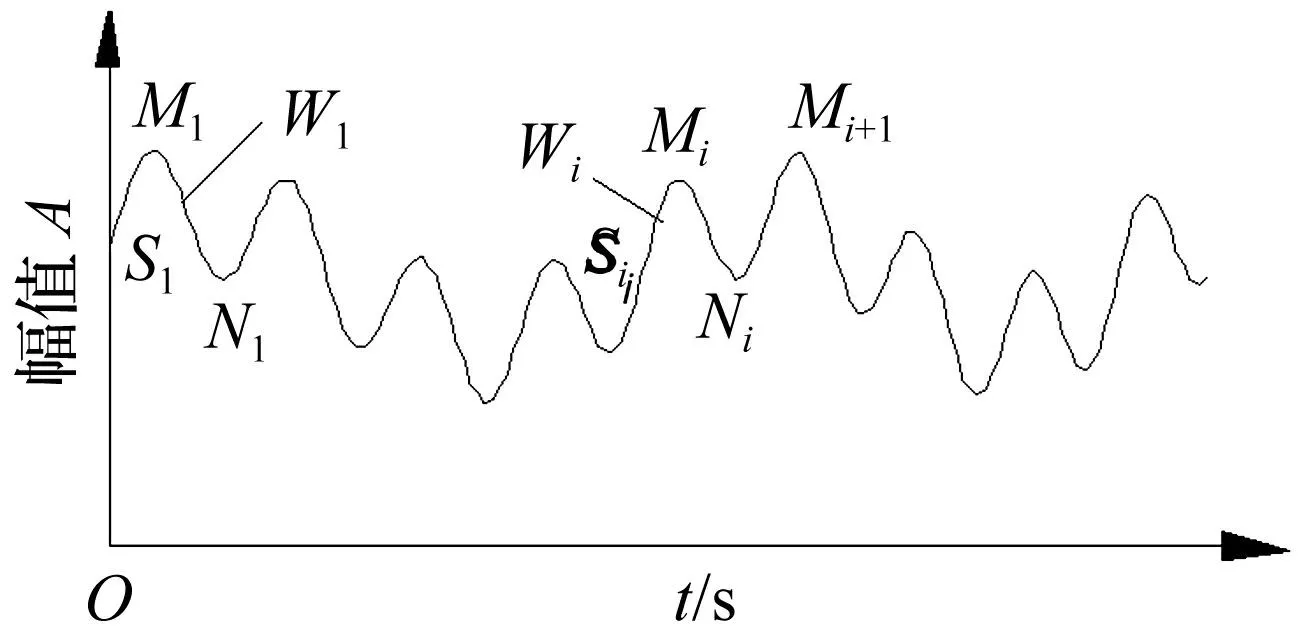
图1 波形匹配示意图 Fig.1 Waveform matching schematic diagram
(3)依次以M(2),…,M(m)为中心定义与w1同样长度的子波形wi(i≥2),wi={x(tmaxi-(tmax1-t1)), …,x(tmaxi), …,x(tmax i+(tmin1-tmax1))}。分别求w1与wi的相关系数值xg作为两个波形的匹配系数,其中
(19)
式中:E[•]表示数学期望,μw1和μwi分别为波形w1和wi的均值,δw1和σwi分别为原信号w1和wi的标准差。
(4)取xg绝对值最大的子波形wi为w1的最佳匹配波形,将wi前的信号数据延拓到x(t1)左侧,延拓点数根据需要选择。
(5)按照同样的方式对信号进行右边界延拓。
(6)对延拓后的信号进行HVD分析,根据原始信号的长度及在原始信号在延拓信号中对应的位置截取分析结果。
3仿真信号分析
仿真信号1:考察一两分量调频信号
x1(t)=sin(2π100t+cos(2π5t))+
0.5sin(2π200t+cos(2π40t))
(20)
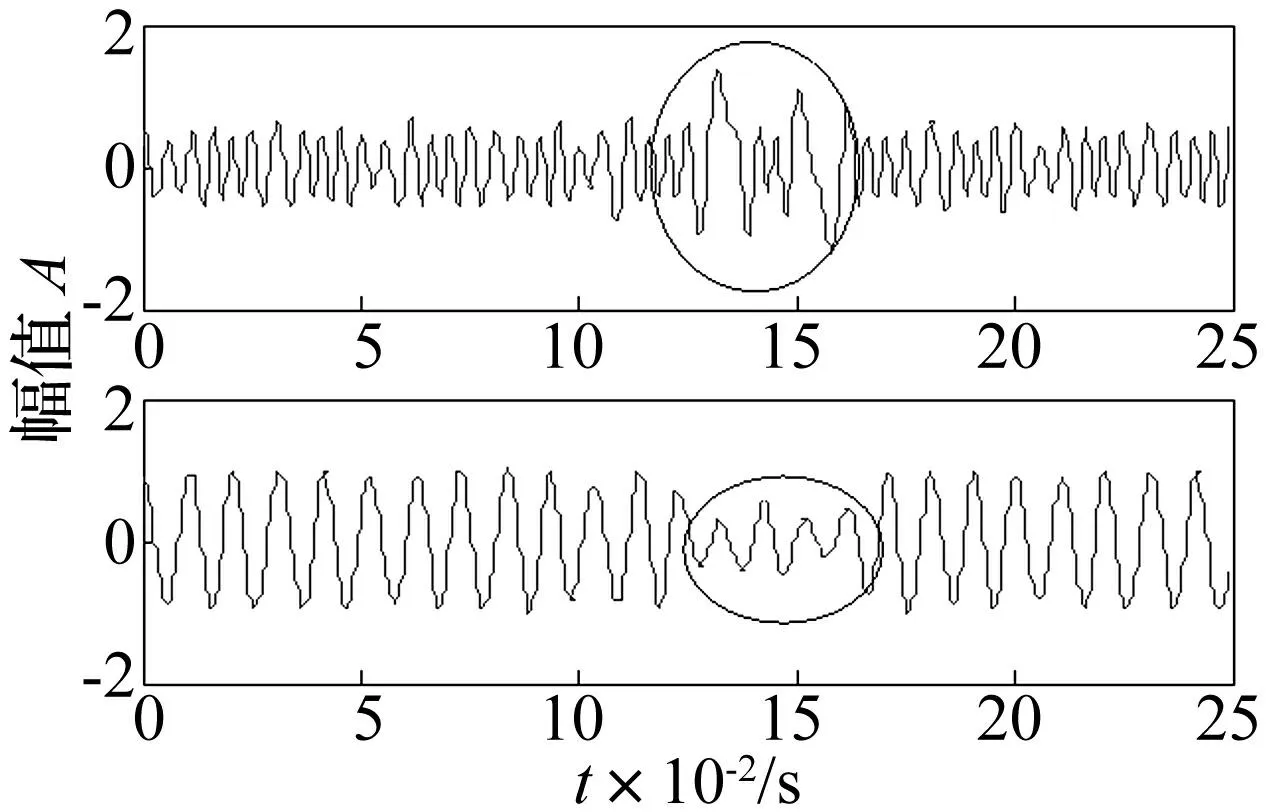
图2 x 1(t)的EMD分析结果 Fig.2 EMD analysis results of x 1(t)
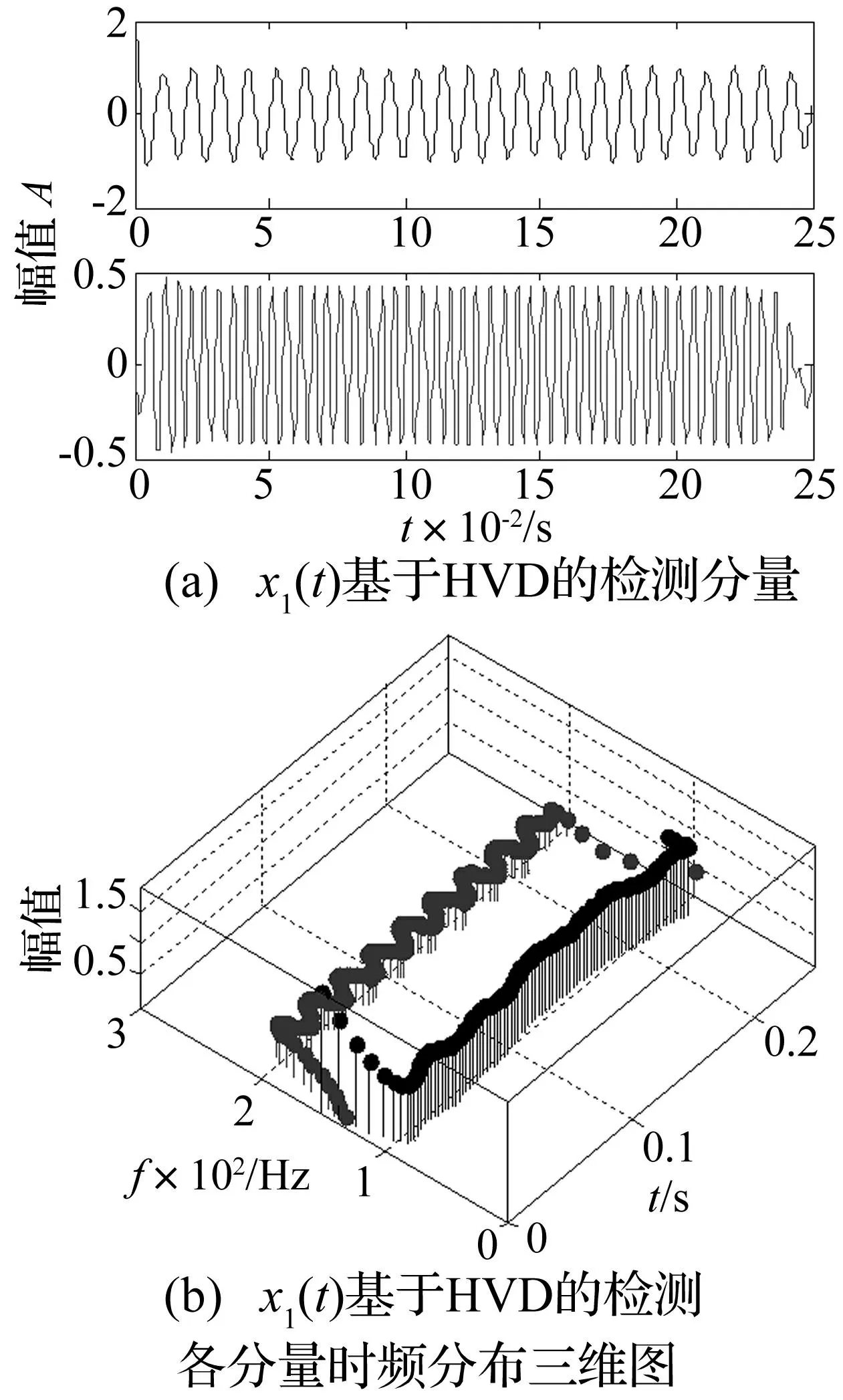
图3 x 1(t)直接进行HVD分析结果 Fig.3 HVD analysis of x 1(t) without improving
式中:t[0,0.25],信号采样频率fs=4 096 Hz。图2为信号经EMD分析得到的前两个IMF分量,两个分量分别出现了一定程度的模态混叠和幅值失真现象。图3(a)为x1(t)直接用HVD方法分析得到的两个分量,图3(b)为对应的时频分布三维图。从分析结果中看出HVD方法克服了EMD方法的模态混叠和幅值失真问题,但存在明显的边界效应问题。并且随着分解过程的继续,第2个分量的端点效应比第1个分量更为明显。图4(a)、图4(b)分别为本文改进的HVD方法对x1(t)分析得到的分量和时频分布三维图,两个分量的边界效应得到抑制,使得时频分析结果更加准确。
仿真信号2:考察一两分量调幅调频信号
x2(t)=(2+0.5cos(10πt))sin(300πt+cos(20πt))+
(1+0.4cos(20πt))sin(900πt+cos(40πt))
(21)
分析时间t[0,1],信号采样频率fs=2 048 Hz。图5、图6分别为直接用HVD方法和改进HVD方法对x2(t)的分析结果。可见HVD方法有效提取了x2(t)两个分量的时频信息,同时经过改进有效克服了HVD方法自身的边界效应。
仿真信号以两组多分量调制信号为例验证了HVD方法对多分量非平稳信号的时频分析能力。齿轮、轴承、转子等旋转机械元件的故障振动信号通常为多分量非平稳信号,HVD方法为此类机械元件的故障特征提取和故障类型判断提供一种新的途径。
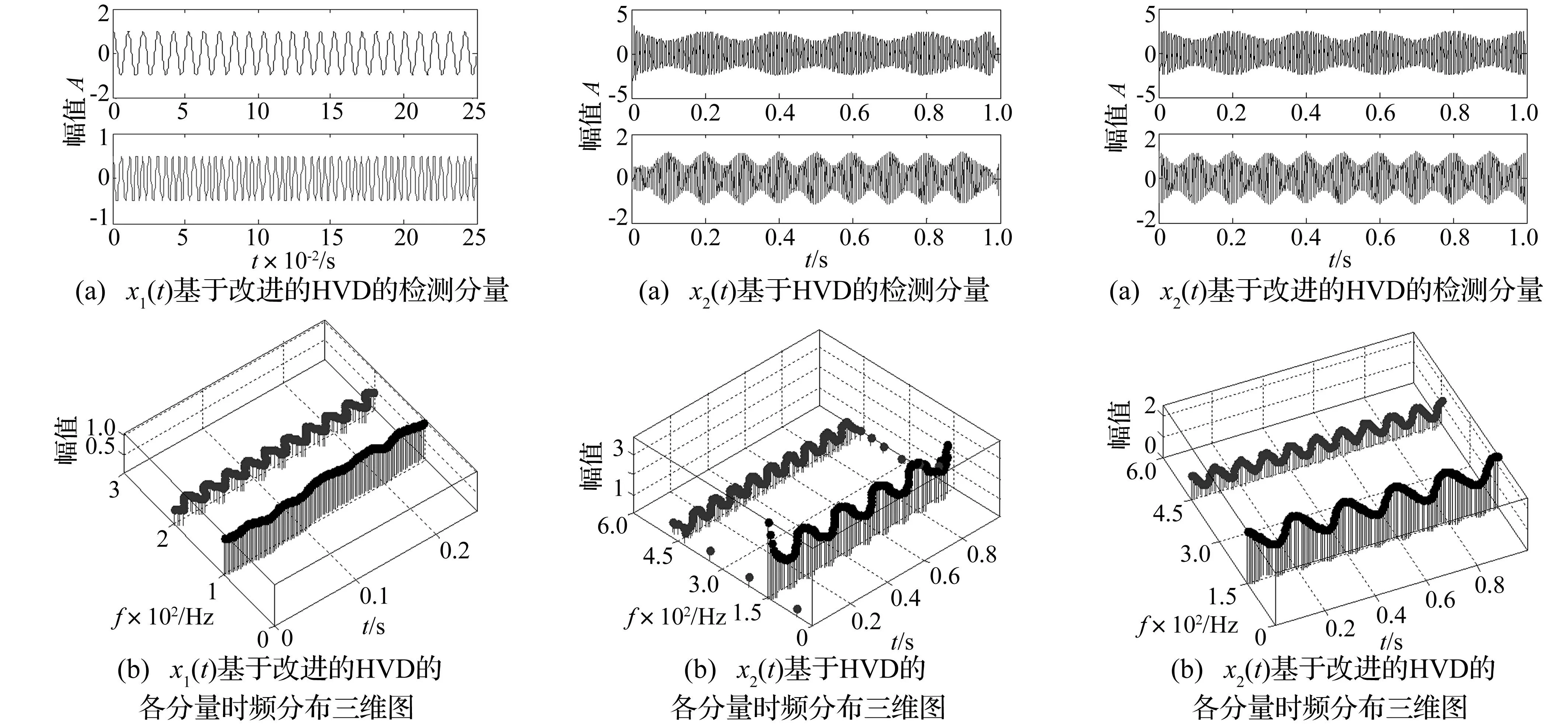

图4 x1(t)基于改进的HVD分析结果Fig.4Analysisofx1(t)basedonimprovedHVD图5 x2(t)直接进行HVD分析结果Fig.5HVDanalysisofx2(t)withoutimproving图6 x2(t)基于改进的HVD分析结果Fig.6Analysisofx2(t)basedonimprovedHVD
4油膜涡动故障诊断实例
利用Bently RK-4转子实验台模拟了2 800 r/min转速下转子系统油膜涡动故障。实验数据由美国Iotech 公司生产的 ZonicBook/618E信号采集设备采得,采样频率为1 280 Hz,采样点数为1 024。
油膜涡动是转子轴颈在轴承运动过程由于受到油膜力的作用,转子绕自身轴心旋转,同时轴心又绕轴承中心连线回转的一种运动形式,涡动频率约为转速的0.47倍[11]。
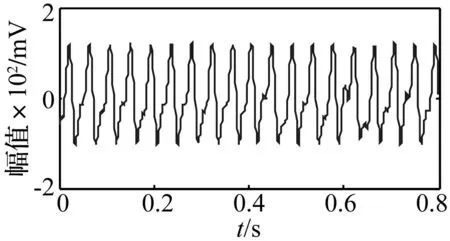
图7 油膜涡动故障信号时域波形 Fig.7 Time domain waveform of oil whirl
图7为转子油膜涡动故障信号的时域波形。图8(a)为油膜涡动故障信号运用改进的HVD方法分解得到的两个分量,第一个分量对应涡动信号,第二个分量对应基频信号。图8(b)为对应的时频分布三维图,两个分量的瞬时频率分别为23.25 Hz、46.65 Hz,涡动频率近似为基频的一半。可见本文方法有效提取了实验转子系统油膜涡动的故障特征。图9为直接HVD方法的分析结果,虽然也提取到了涡动信号和基频信号两个分量,体现出油膜涡动的故障特征,但端点效应比较明显,极大影响了HVD方法的分析精度。为突出本文方法的优点,同时对油膜涡动故障信号进行了EMD分解,结果如图10所示,产生6个IMF分量。其中IMF1、IMF2分别对应基频信号和涡动信号。与改进的HVD方法相比,两个包含故障特征信息的IMF分量均出现了一定程度的模态混叠和幅值失真现象,代表的物理过程被干扰,不能体现设备的真实状态。对比分析表明改进的HVD方法分解效率高、分解速度快。提取的故障信息更加直观、准确。
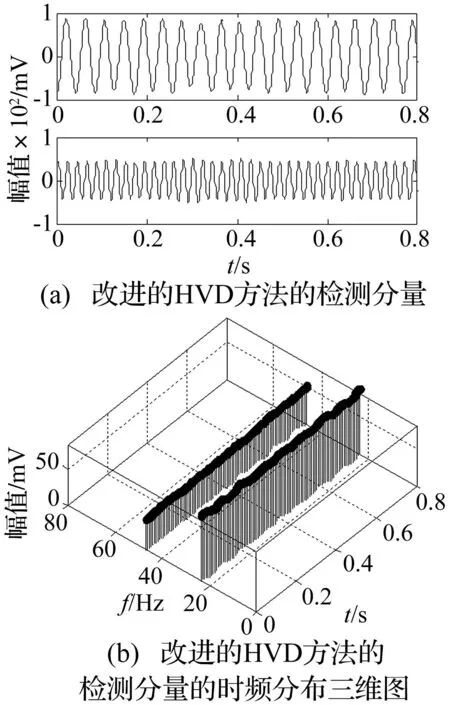
图8 改进的HVD方法的分析结果 Fig.8 Improved HVD analysis
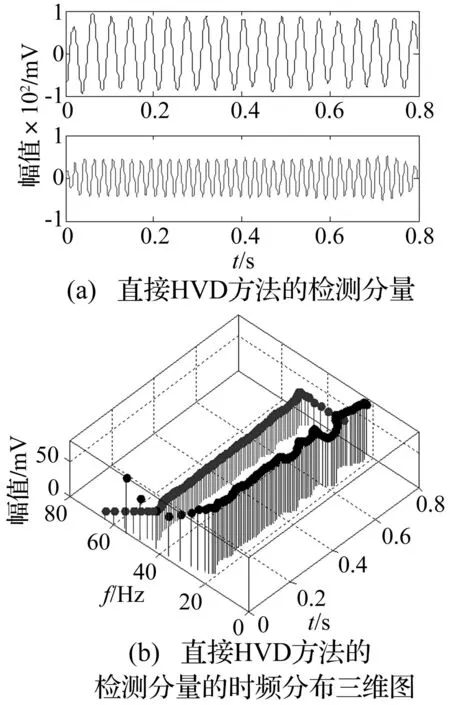
图9 直接进行HVD分析结果 Fig.9 HVD analysis without improving
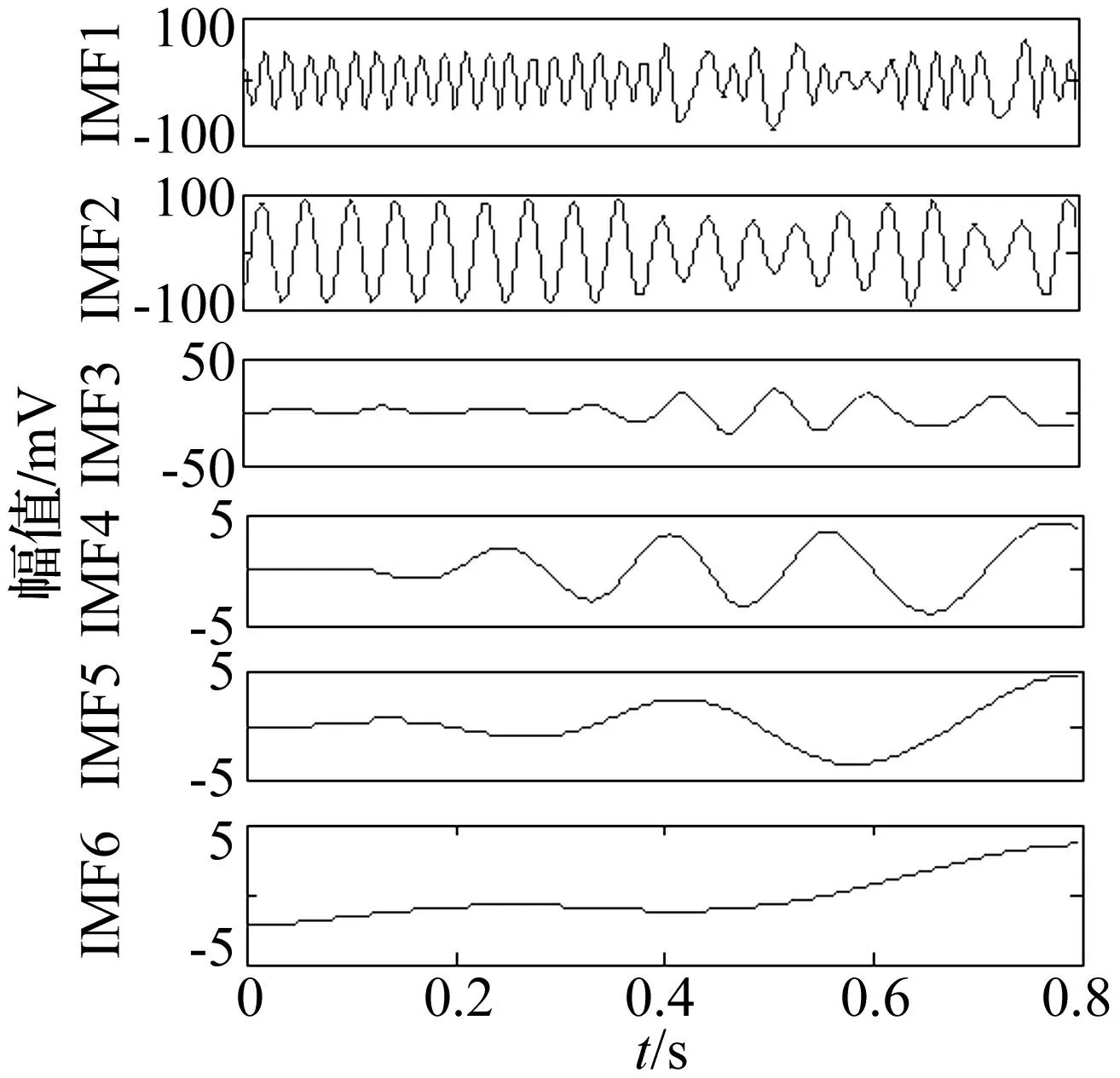
图10 油膜涡动信号的EMD分析结果 Fig.10 Analysis results of EMD for oil whirl signal
5结论
本文介绍了一种多分量非平稳信号的时频分析新方法——希尔伯特振动分解(HVD)。该方法以Hilbert变换为基础,可以自适应地将原始振动信号的各个分量分解出来,通过检测各个分量的频率、幅值和相位信息,提取振动信号的故障特征,具有分解精度高、分解速度快的优点。针对HVD方法自身的边界效应问题,提出一种基于相关系数准则的波形匹配边界延拓法对HVD方法进行改进。通过仿真信号分析验证了HVD方法对多分量信号的分解能力和本文方法对HVD边界效应的改进效果。最后给出转子系统油膜涡动故障诊断实例,取得很好的分析效果,为机械故障诊断提供一种新的途径。
参考文献
[1]程军圣,杨宇,于德介.基于广义解调时频分析的多分量信号分解方法[J]. 振动工程学报, 2006, 19(6):563-568.
CHENG Jun-sheng, YANG Yu, YU De-jie. A multi-component signal decomposition method based on the generalized demodulation time-frequency analysis [J]. Journal of Vibration Engineering, 2006,19(6):563-568.
[2]来五星,轩建平,史铁林,等.Wigner-Ville时频分布研究及其在齿轮故障诊断中的应用[J]. 振动工程学报, 2003, 16(2):247-250.
LAI Wu-xing, XUAN Jian-ping, SHI Tie-lin, et al. Research of Wigner-Ville time frequency and application in detecting gear pinion fault[J]. Journal of Vibration Engineering, 2003, 16(2):247-250.
[3]张晓峰,李功燕.应用小波分析提取故障诊断信号的特定频段[J].振动与冲击,2004, 23(4):47-50.
ZHANG Xiao-feng, LI Gong-yan. Review on structural control for offshore platforms [J]. Journal of Vibration and Shock, 2004, 23(4):47-50.
[4]Huang N E, Shen Z, Long S R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc. R. Soc. Lond. A, 1998, 454:903-995.
[5]郭琦,刘卜瑜,史立波,等.基于二次 EEMD的Wigner-Ville分布旋转机械故障信号分析及试验研究[J].振动与冲击,2012, 31(13):129-133.
GUO Qi, LIU Bo-yu, SHI Li-bo, et al.Experimental study and fault signals analysis of machinery based on dual EEMD and Wigner-Ville distribution [J]. Journal of Vibration and Shock, 2012, 31(13):129-133.
[6]向玲,唐贵基,胡爱军.旋转机械非平稳振动信号的时频分析比较[J].振动与冲击,2010, 29(2):42-45.
XIANG Ling, TANG Gui-ji, HU Ai-jun.Vibration signal s time-frequency analysis and comparison for a rotating machinery [J]. Journal of Vibration and Shock, 2010,29(2):42-45.
[7]罗颂荣,程军圣,杨宇.基于本征时间尺度分解和变量预测模型模式识别的机械故障诊断[J].振动与冲击,2013, 32(13):43-48.
LUO Song-rong, CHENG Jun-sheng, YANG Yu. Machine fault diagnosis method using ITD and variable predictive model-based class discrimination [J]. Journal of Vibration and Shock, 2013, 32(13):43-48.
[8]Feldman M. Time-varying vibration decomposition and analysis based on the Hilbert transform [J]. Journal of Sound and Vibration, 2006, 295:518-530.
[9]刘慧,刘国海,沈跃.采用希尔伯特振动分解的非整数次谐波检测新方法[J].高电压技术,2009,35(7):1758-1762.
LIU Hui, LIU Guo-hai, SHEN Yue. Novel method for non integer harmonics measurement using Hilbert vibration decomposition [J]. High Voltage Engineer, 2009, 35(7):1758-1762.
[10]Feldman M. Theoretical analysis and comparison of the Hilbert transform decomposition methods[J]. Mechanical Systems and Signal Processing, 2008, 22:509-519.
[11]向玲,朱永利,唐贵基.HHT 方法在转子振动故障诊断中的应用[J].中国电机工程学报,2007,27(35):84-88.
XIANG Ling, ZHU Yong-li, TANG Gui-ji. Application of Hilbert-Huang Transform method in vibration faults diagnosis for rotor system [J]. Proceedings of the CSEE, 2007, 27(35):84-88.

