通过模态滤波实现阵列式传感器系统的故障诊断

第一作者朱峤男，硕士生，1989年生

通信作者毛崎波男，博士，副教授，1975年生

通过模态滤波实现阵列式传感器系统的故障诊断

朱峤，毛崎波

(南昌航空大学飞行器工程学院，南昌330063)

摘要：基于结构振动响应特性利用改进的模态滤波方法对阵列式传感器系统进行故障诊断。在梁结构表面均匀布置一组加速度计，利用模态振型对该系统的输出信号进行重构，将重构信号与实际信号之间的曲率误差作为敏感参数，对系统中的模拟故障传感器进行检测与识别，并加以实验验证。数值计算和实验结果表明：改进的模态滤波方法不仅可以直接有效地对传感器系统进行实时故障监测，而且该方法与外界激励力位置无关，具有良好的工程应用前景。

关键词：模态滤波;曲率误差;阵列式传感器;故障诊断

收稿日期：2013-11-29修改稿收到日期：2014-02-20

中图分类号:TP212.6文献标志码：A

基金项目：国家自然科学

基金项目：国家自然科学基金(11227201, 11372199)

Fault detection of a sensor array using modal filtering method

ZHUQiao,MAOQi-bo(School of Aircraft Engineering, Nanchang University of Aeronautis, Nanchang 330063, China)

Abstract:By using the modal filtering method, a modified sensor fault detection approach based on structural dynamic characteristics was presented. An array of accelerometers attached on the surface of a beam was taken as sensors. The differences between the reconstructed signals with modal filtering from the output signals of the beam system and the real measured signals were obtained, then the curvature errors were taken as sensitive indexes to detect and identify the simulated fault sensor of the sensor system. The numerical simulations and experimental results showed that the proposed method can be used to detect the fault sensor system efficiently; furthermore, this method is independent upon the location of an excitation and it can be used for real-time monitoring systems.

Key words:modal filtering; error of curvature; sensor array; fault detection

近年来，随着传感器技术的发展，其大规模阵列系统越来越受到关注。其中，基于结构振动响应和动力特性的阵列式传感器系统在结构健康监测(Structural Health Monitoring)领域得到了广泛研究[1-4]。对于一个可靠的实时振动监测系统而言，传感器是信息获取的主要装置。如果传感器出现故障(如性能蜕化、增益故障或失效等)，会对监测、故障诊断结果带来严重影响，产生误诊断、误报警甚至不可估量的损失。因此，对传感器系统进行自身故障诊断问题的研究就显得尤为重要。

传感器故障诊断(Sensor Fault Detection)技术即通过各种数据处理方法分离出故障信息，在传感器系统中检测并识别出故障传感器，以避免其带来的严重后果。最基本的诊断方法就是人工定期的校准，但这不仅浪费人力、物力，而且在大多数情况下根本无法进行。近来，有学者基于结构振动响应特性，利用传感器系统的冗余信息对其进行故障诊断[5-10]。基于不同的冗余信息，产生出不同的诊断方法和敏感参数。Dunia等[5]和Kerschen等[6]基于主成分分析法(Principal Component Analysis, PCA)分别将传感器有效性指标(Sensor Validity Index, SVI)和主空间之间的夹角(Principal Angle,PA)作为敏感参数对故障传感器进行检测、隔离和重构。Kullaa等[7-8]提出利用最小均方误差估计(Minimum Mean Square Error, MMSE)对传感器系统进行故障诊断，该方法直接通过对测量数据进行处理来实现传感器故障诊断而不需要预先获得任何结构模态信息。

上述方法都是通过处理频域下的冗余信息对传感器系统进行故障诊断，然而传感器的实时测量均建立在时域基础上进行，得到的时域信号需经过傅里叶变化转换为频域信号才能进行处理，这使得对传感器系统的故障监测不能实时进行。Friswell和Inman[9-10]介绍了一种时域下的基于模态滤波(Modal Filtering)进行传感器故障诊断的方法，将实际输出与重构输出之间的平均误差向量(Average Error Vector)作为敏感参数，对传感器系统进行故障检测和识别。然而该方法建立在子集选择(Subset Selection)算法的基础上，对于大规模传感器布置网络，这种方法同样不能实现实时故障监测。

本文在文献[9]的基础上，对Friswell提出的模态滤波方法进行改进，将曲率误差向量作为敏感参数对传感器系统进行故障诊断。该方法不仅提高了误差向量在传感器故障诊断过程中的敏感程度，而且不需要利用子集选择算法对大规模传感器进行划分，可以直接有效地检测并识别出故障传感器，进行实时监测。

本文首先简要介绍了基于模态滤波方法对传感器系统进行故障诊断的基本原理；然后以悬臂梁为例，利用改进的模态滤波方法对多种工况下的传感器故障诊断进行数值模拟；最后以10个加速度计均布组成传感器阵列进行实验验证。

1基本理论

假设在任意边界条件下的弹性梁结构表面均匀布置N个相同的传感器，受到外界激励时，其在任意时刻t的振动响应Y(t)可以由模态振型线性表示为：

(1)

式中:Y(t)=[Y1(t)…YN(t)]T为传感器系统t时刻的输出向量，Φ=[φ1…φM]为梁的模态振型矩阵，q(t)=[q1(t)…qM(t)]T为t时刻梁结构的模态坐标向量，M为所取最大结构模态序数。

阵列式模态传感器的工作原理如图1所示，其输出可以线性表示为每个传感器输出的加权和。假设传感器系统正常工作，为了使其输出等于模态坐标向量q(t)，即：

(2)

式中:Wnm为第n号传感器对应第m阶模态坐标的加权系数。

图1　阵列式模态传感器原理图 Fig.1 Theory of the modal sensor array

将式(1)代入式(2)整理得：

W=Φ+

(3)

式中:Φ+=[ΦHΦ]-1ΦH为矩阵Φ的伪逆，上角标H表示共轭转置。

(4)

将式(4)代入式(1)，即对系统输出进行重构，可得：

(5)

故模态传感器实际输出与重构输出之间的误差向量εt可以表示为：

(6)

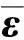
(7)

式中T为结构振动响应的采样点数。

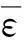
(8)

式中:k(x)为插值函数的曲率函数。

取k(xi) (i=1,2…N)组成曲率误差向量k=[k1,k2…kN]T作为敏感参数来对传感器系统进行故障诊断。

2数值分析

为了验证利用改进的模态滤波方法对传感器系统进行故障诊断的可行性，本文以悬臂梁为例布置加速度计阵列进行数值计算。设悬臂梁长度Lx=620 mm，宽度Ly=55 mm，厚度Lz=8 mm，弹性模量G=210 GN/m2，密度ρ=7 850 kg/m3，阻尼比ξ=0.01。如图2所示，该悬臂梁沿长度方向均匀划分为10个单元，将加速度计布置在每个单元中心位置，激励力f为点激励，作用于xf。

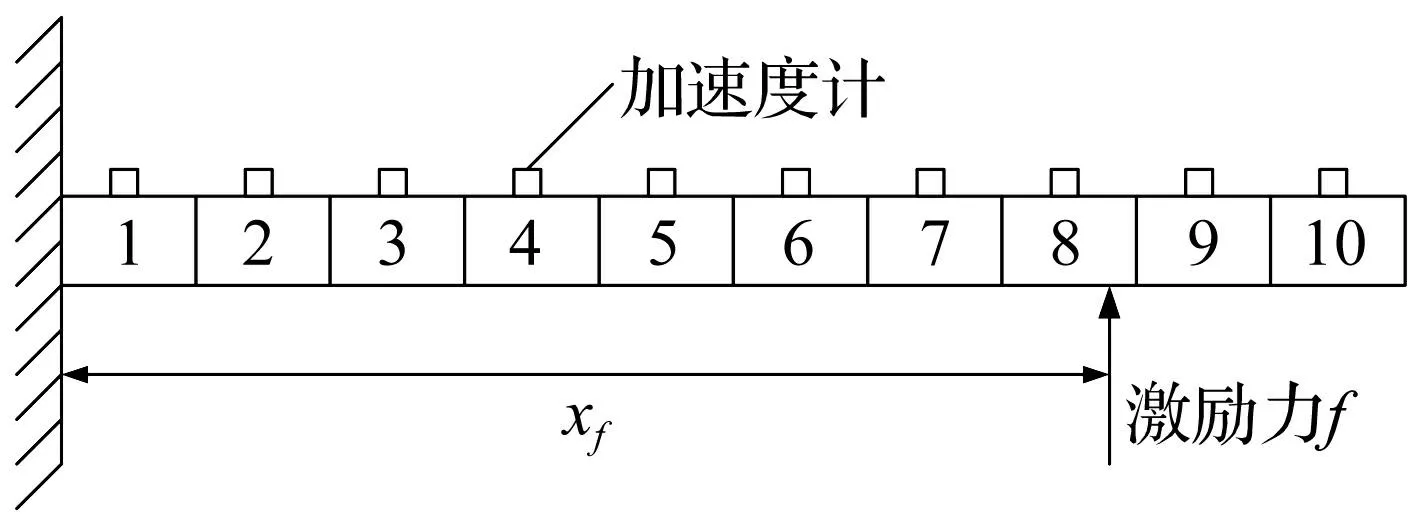
图2　悬臂梁示意图 Fig. 2 Cantilever beam with an array of accelerometers

首先，假设激励力f位于xf=620 mm处，如果6号加速度计发生故障，依次模拟其输出相比正常情况下减少5%、10%和20%，三种工况均取前三阶模态振型进行输出重构，取10 000个结构振动时域响应点参与平均误差向量计算。

图3(a)为模态传感器在正常工作和发生故障(6号加速度计输出减少10%)情况下，通过式(2)和(4)计算得到的第一阶模态坐标的时域结果。注意到图中传感器故障产生的误差并不明显，为了进一步分析，图3(b)给出了其频域表示。从图中可以看出，故障传感器输出产生的误差会引起模态传感器实际测得模态坐标在其他固有频率处出现峰值。

图4表示6号传感器在三种模拟故障下系统的曲率误差向量，从图中可以看出，六号传感器对应曲率误差偏离零值较大，且引起了附近传感器对应的曲率误差反方向偏离零值，由此可判断6号加速度计发生故障。同时，通过对比三种工况下的诊断结果可以发现，即使是传感器输出发生微小变化故障，对应曲率误差偏离零值的程度与非故障传感器相比仍然较大，这说明利用本文方法对传感器系统进行故障检测与识别是可行的，且需求计算量小，可以实现实时监测。

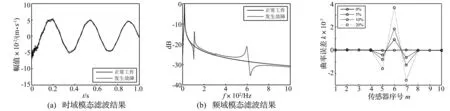
图3 模态传感器正常工作与发生故障情况下第一阶模态坐标Fig.3Thefirstmodalcoordinateofthebeam图4不同程度故障下模态传感器的曲率误差向量(数值模拟)Fig.4Numericalresultsofcurvatureerrorvectorwithdifferentextentsofmodalsensorfault

图5表示6号传感器在10%输出减少模拟故障下，激励力分别位于xf=3/10Lx，5/10Lx，7/10Lx和9/10Lx时模态传感器的曲率误差向量。从图中可以发现，激励力位置改变不影响传感器故障的检测与识别，这说明本文方法对传感器系统进行故障诊断与外界激励力位置无关。

图5　不同激励力位置模态传感器的曲率误差向量 Fig.5 Numerical results of curvature error vector with different locations of excitation

3实验研究

为了进一步验证利用曲率误差对传感器系统进行故障诊断的有效性，取长620mm、宽55mm、厚8mm的悬臂梁结构进行实验研究。在梁上均匀布置10个加速度计，梁自由端用力锤施加激励。数据采集过程中采样频率为1000Hz，采样长度为4096个采样点，利用YE6251动态分析仪分别测量得到10个加速度计的时

域输出信号，手动调整将6号加速度计的输出依次减少5%、10%和20%，作为故障传感器，分别计算模态传感器在这三种工况下的曲率误差向量。图6给出了接近实验梁自由端的10号加速度计在激励力作用下的时域输出。

图7给出了6号传感器在三种故障下系统的曲率误差向量，从图中可以发现，虽然非故障传感器对应曲率误差偏离零值程度与数值模拟结果相比有所增加，这主要是由实验过程中外界噪声干扰所致，但故障传感器对应曲率误差偏离零值程度远大于非故障传感器，且引起邻近传感器对应的曲率误差反方向偏离零值，由此仍可准确判断出6号加速度计发生故障。

图8给出了表示6号传感器在10%输出减小模拟故障下，激励力分别位于xf=3/10Lx，5/10Lx，7/10Lx和9/10Lx时模态传感器的曲率误差向量。从图中可以发现，激励力位置的变化对故障诊断结果几乎没有影响，实验结果验证了本文方法对传感器系统进行故障诊断与外界激励力位置无关。

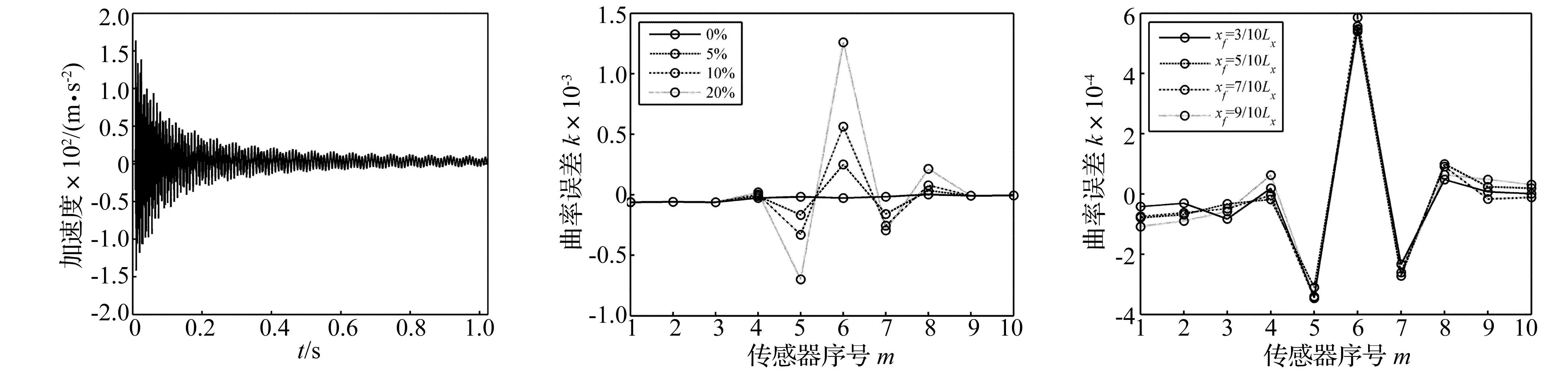
图6 悬臂梁自由端响应Fig.6Responseatcantileverbeamtip图7 不同程度故障下模态传感器的曲率误差向量(实验验证)Fig.7Experimentalresultsofcurvatureerrorvectorwithdifferentextentsofmodalsensorfault图8 不同激励力位置模态传感器的曲率误差向量(实验验证)Fig.8Experimentalresultsofcurvatureerrorvectorwithdifferentlocationsofexcitation

4结论

本文提出通过改进的模态滤波方法，将曲率误差作为敏感参数对传感器系统进行故障诊断，并分别通过数值模拟和实验验证了该方法的可行性。数值模拟和实验结果表明，利用曲率误差不仅可以有效的检测并识别出故障传感器，而且数据处理全部在时域下直接进行，需求计算量小，可以实现实时监测。同时，数值分析结果还表明本文方法虽然基于结构振动响应，但与外界激励位置无关。需要指出的是，本文方法必须预先知道结构的模态振型，有研究表明结构损伤有可能会使传感器输出产生类似于图3的信号误差[1,11]，如何对传感器故障和结构损伤进行区分识别将是我们未来研究的重点。

参考文献

[1]Kullaa J. Distinguishing between sensor fault, structural damage, and environmental or operational effects in structural health monitoring[J]. Mechanical Systems and Signal Processing, 2011, 25(8): 2976-2989.

[2]Yoon M K, Heider D, Gillespie Jr J W, et al. Local damage detection with the global fitting method using operating deflection shape data[J]. Journal of Nondestructive Evaluation, 2010, 29(1): 25-37.

[3]聂彦平, 毛崎波, 张炜. 基于 PVDF 传感器和工作曲率变形实现裂纹梁裂纹检测[J]. 传感技术学报, 2013,26(1): 138-142.

NIE Yan-ping, MAO Qi-bo, ZHANG Wei. Crack detection for beam structures based on operating curvature deflection shape using PVDF sensors[J]. Chinese Journal of Sensor and Actuators, 2013, 26(1): 138-142.

(下转第65页) J. Distinguishing between sensor fault, structural damage, and environmental or operational effects in structural health monitoring[J]. Mechanical Systems and Signal Processing, 2011, 25(8): 2976-2989.

[2]Yoon M K, Heider D, Gillespie Jr J W, et al. Local damage detection with the global fitting method using operating deflection shape data[J]. Journal of Nondestructive Evaluation, 2010, 29(1): 25-37.

[3]聂彦平, 毛崎波, 张炜. 基于 PVDF 传感器和工作曲率变形实现裂纹梁裂纹检测[J]. 传感技术学报, 2013,26(1): 138-142.

NIE Yan-ping, MAO Qi-bo, ZHANG Wei. Crack detection for beam structures based on operating curvature deflection shape using PVDF sensors[J]. Chinese Journal of Sensor and Actuators, 2013, 26(1): 138-142.

[4]毛崎波. 通过 PVDF 阵列测量体积位移的实验研究[J]. 传感技术学报, 2012, 25(8): 1054-1058.

MAO Qi-bo. Experimental research on the volume displacement sensor using PVDF array[J]. Chinese Journal of Sensor and Actuators, 2012, 25(8): 1054-1058.

[5]Dunia R, Qin S J, Edgar T F, et al. Identification of faulty sensors using principal component analysis[J]. AIChE Journal, 1996, 42(10): 2797-2812.

[6]Kerschen G, De Boe P, Golinval J C, et al. Sensor validation using principal component analysis[J]. Smart Materials and Structures, 2005, 14(1): 36.

[7]Kullaa J. Sensor fault identification and correction in structural health monitoring[C]//Proceedings of ISMA2006, International Conference on Noise and Vibration Engineering,Leuven, Belgium. 2006: 873-884.

[8]Kullaa J. Sensor validation using minimum mean square error estimation[J]. Mechanical Systems and Signal Processing, 2010, 24(5): 1444-1457.

[9]Friswell M I, Inman D J. Sensor validation for smart structures[J]. Journal of Intelligent Material systems and Structures, 1999, 10(12):973-982.

[10]Friswell M I, Inman D J. Sensor validation for smart structures[C]//Fifth European Conference on Smart Structures and Materials, Glasgow, Scotland. 2000: 150-161.

[11]Karaiskos G, Tondreau G, Figueiredo E, et al. Application of modal filters for damage detection in the presence of non-linearities[C]//Proceedings of 6th European Workshop on Structural Health Monitoring, Dresden, Germany. 2012:Th.2.D.2.

[12]Bahlous S E O, Abdelghani M, Smaoui H, et al. A modal filtering and statistical approach for damage detection and diagnosis in structures using ambient vibrations measurements[J]. Journal of Vibration and Control, 2007, 13(3): 281-308.

[13]金卫民, 神显豪, 巩传雷. 一种基于 SVR 的传感器系统故障诊断方法[J]. 微计算机信息, 2007, 23(7): 226-227,230.

JIN Wei-min, SHEN Xian-hao, GONG Chuan-lai. Sensor fault diagnosis system base on support vector regression[J]. Microcomputer Information, 2007, 23(7): 226-227,230.