基于MID算法的组合切片分析在滚动轴承故障诊断中的应用

第一作者马增强男，博士，教授，1975年 4月生

通信作者杨绍普男，博士，教授，博士生导师，1962年出生

基于MID算法的组合切片分析在滚动轴承故障诊断中的应用

马增强1， 梁建华1， 杨绍普2

(1. 石家庄铁道大学电气与电子工程学院，石家庄050043；2．石家庄铁道大学交通环境与安全工程研究所，石家庄050043)

摘要：调制密度分布(MID) 作为谱相关密度的开放性推广，能够很好地解决离散或者随机载波调制信号的检测问题,然而该算法在判定轴承故障前需要大量计算描述矩阵来估计调制密度因子，不能满足工业生产的实时性要求。为此，提出基于MID算法的组合切片分析方法，首先根据转速的波动范围，确定故障特征频率相对于理论值的波动范围，然后给定选择性因数(Δf )的范围并计算信号的MID组合切片带，最后通过切片带之间的能量对比确定轴承故障类型。该分析方法不仅对噪声不敏感，而且有效地减少了计算量，满足了实时性要求。随后，分别采用仿真信号和QPZZ-II系统(滚动轴承故障模拟实验平台)的实测数据，对MID组合切片分析方法进行了实验验证，并与包络解调分析进行了对比。实验结果表明，该方法对滚动轴承外圈、内圈和滚动体故障的检测精度更高。

关键词：滚动轴承；MID算法；组合切片分析；故障诊断

收稿日期：2014-07-16修改稿收到日期：2014-09-25

中图分类号:TH165.3文献标志码：A

Application of combined slice analysis based on MID algorithm in fault diagnosis of rolling element bearings

MAZeng-qiang1,LIANGJian-hua1,YANGShao-pu2(1. Shjiazhuang Railway University, Shijiazhuang 050043, China；2. Research Institute of Transportation Environment and Safety Engineering, Shijiazhuang Railway University, Shijiazhuang 050043, China)

Abstract:As a generalization of spectral correlation density, modulation intensity distribution (MID) can be used to extract amplitude modulations of either discrete signals or random ones satisfactorily. However, the computational effort of modulation intensity factor in MID is so heavy that it can not satisfy the real time request of industrial applications. Here, a new method, combined slice analysis based on MID (C-SMID), was proposed to detect the characteristic frequency of bearing faults. Firstly, the speed variation range of a rolling bearing was used to decide the possible frequency fluctuation range of bearing fault signals. Then, the range of the selectivity factor △f was set and the character slices of MID were calculated out. Finally, the bearing fault type was judged based on the signal energy comparison between different slices. Comparing with the original MID, the new method had a better anti-noise property and a less amount of calculation. In order to verify the feasibility and superiority of the new method, several comparative experiments between it and the common envelope demodulation method were performed with the simulated signals and the measured ones acquired from a rolling bearing fault simulation test platform QPZZ-II. The test results showed that the new method has higher detection precision for bearing faults of inner race, outer race and rolling parts.

Key words:rolling element bearing; MID algorithm; combined slice analysis; fault diagnosis

旋转机械的运动多数为周期性的旋转和往复，因而在振动信号中存在大量的随机性和周期性成分，其二阶统计特性参量因随时间变换而呈现非平稳特性。轴承、齿轮等复杂部件发生故障时，其载波(调制源)往往是离散或者随机的，调制的信号常常淹没在强背景噪声之中，难于分离提取。基于经典Fourier变换的包络解调分析方法，假设被分析信号具有平稳特性的前提下对信号做全局性变换。虽然包络解调分析方法能够在包络谱上突出故障特征，但缺少时频局部细节信息，而且分析过程中预处理带通滤波需要主观确定，因而对微弱故障和被强背景噪声淹没的振动信号的特征提取往往是失效的。在非平稳领域也有许多重要的研究工作，采用同步平均的方式[1]可以补偿速度的波动并消除噪声，但同时削弱了信号中的调制成分。为了有效解决上述问题，文献[2- 3] 提出了二阶循环平稳信号分析方法并得到证实，一些能够在(f,α)二维频率面解释故障特征的二阶统计指标相继被提出—循环谱密度(CSD)和循环谱相干(CC)。文献[4]应用循环平稳分析方法对典型轴承故障诊断取得了令人满意的效果。Urbanek等[5]提出了调制密度分布(MID)，通过(f,α)双频率平面三维图谱表达在给定选择性因数(△f)的条件下，调制频率α相对于边带滤波器中心频率f(载波频率)的分布关系。文献[6-7]通过遍历所有循环频率和载波频率将循环相干和MID的结果进行集成得到—ICC和IMID。ICC和IMID能够很好地提取故障特征，但在判定故障类型前需要用大量的计算来估计调制密度因子的描述矩阵，不能满足工业生产的实时性要求。为了有效地解决实时性问题，文献[8]和文献[9]分别研究了组合切片分析方法和SACA方法并成功应用于轴承故障诊断之中。为了避免平稳假设前提下时频细节丢失、受噪声影响较大的问题，并克服非平稳分析算法复杂、计算量大的缺点，本文提出了MID组合切片分析方法，该方法计算效率高，对噪声不敏感，在微弱故障特征提取中有较大的优势。

1MID算法原理

为了更好地检测齿轮和轴承故障，Urbanek和Antoni于2012年提出MID算法，算法适用对离散或者随机载波的幅度调制信号的检测，是窄带包络分析的自然延伸。算法的核心就是利用边带滤波器基本思想(如图1所示)抽取潜在的载波成分和相关的调制成分。算法的处理过程可以理解包含△f、f和α三个滤波器组件的滤波过程，时域信号经过滤波器后不仅可以输出包含指定成分、具有高信噪比的调制信号，而且可以输出由频率α间隔开的三个频率分量的关联程度。

图1　边带滤波示意图 Fig.1 Principle of a sideband filter

(1)

其中:xΔf(t,f)代表x(t)滤波后的输出，滤波的频带范围为[f-Δf/2,f+Δf/2]。在实际应用中为了防止频率混叠现象的发生，选择性因数Δf需满足Δf≤α。

为了确定边带滤波器的中心频率f和调制频率α值，需搜索所有可能的f、α值，只有当三个滤波器组件包含了全部的载波和相应的调制成分，才使得调制密度因子的估计达到最大，最大估计对应的就是振动信号的冲击脉冲激起的共振频带和故障特征频率。MID算法的大致流程如图2 所示。从算法流程图可以看出，MID算法引入了一个可以根据用户需要和信号调制特征而自行编制的开放性模块(调制密度因子)—RMS、谱相关和峭度等指示信号中调制成分含量的指标。本文引入谱相关密度的共轭乘积(公式(2))作为调制密度因子。

(2)

其中:

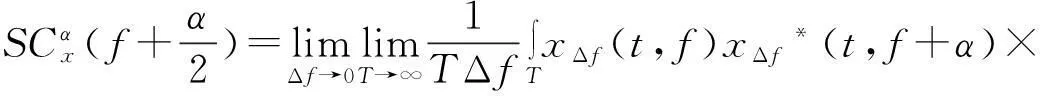
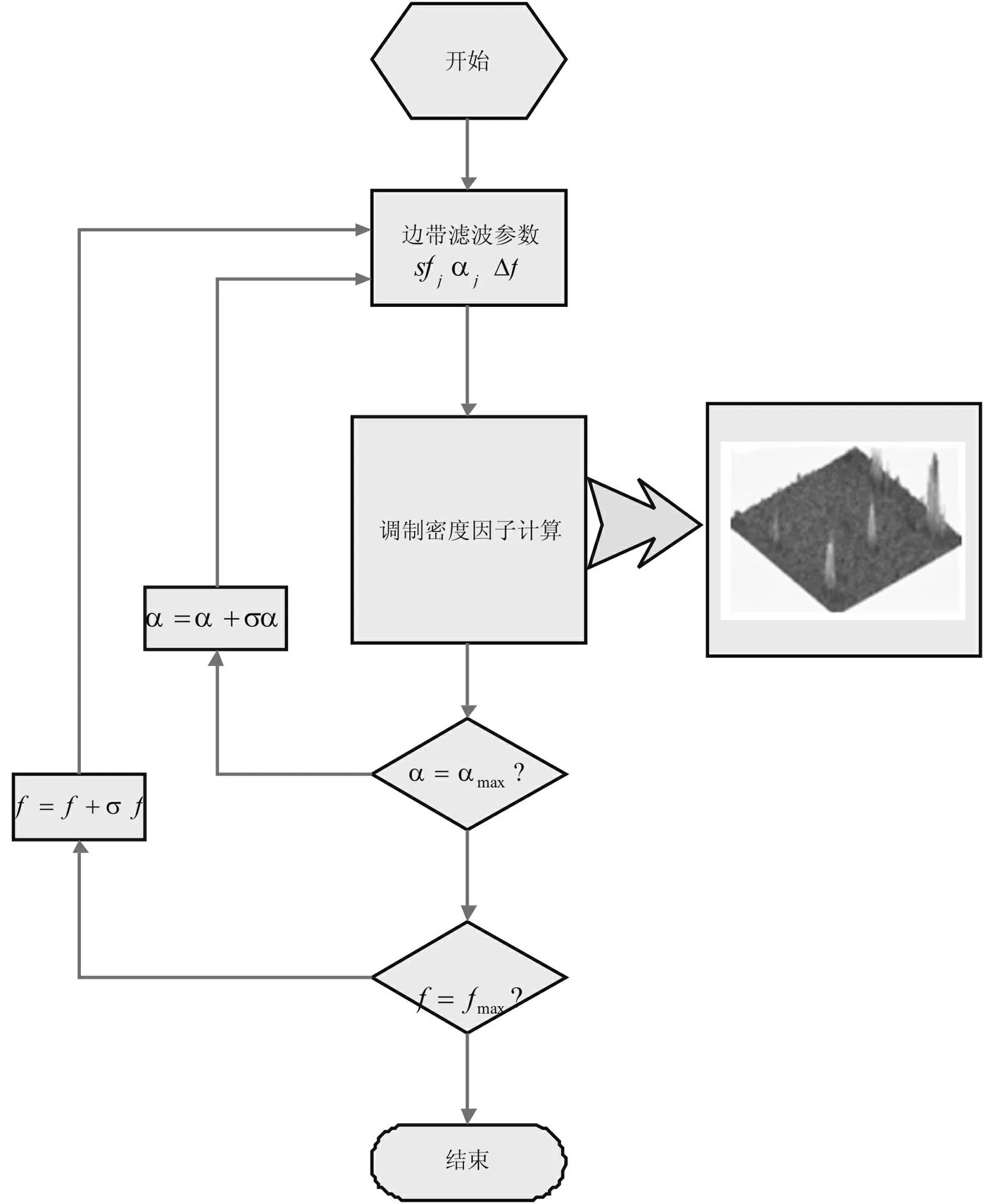
图2　MID算法流程图 Fig.2 Flow chart of MID algorithm

2基于MID算法的组合切片分析原理和流程

2.1方法原理

通过轴承点蚀故障数学模型[2]和式(2)可以推导出模型的强制密度分布如下：

(3)

式中：rq为E{di}的傅里叶变换系数；φτ(α)为{τi}i∈Z概率密度的傅里叶变换系数，α1对应轴承的故障发生频率，α2为轴频或保持架转频引起的{di}的变动频率。仅当循环频率等于故障发生频率α1及其倍频成分,以及围绕α1倍频的以调制频率α2为间距的边带成分时, 调制密度分布存在非零值。点蚀故障模型中的加性噪声经调制密度分布计算后，并没有显现在式(3)中，因而可以看出加性噪声的干扰对点蚀故障的特征提取影响很小。

2.2算法流程

MID算法具有一个衡量信号中调制成分分布情况的估计值(调制密度因子)，这一估计值是Δf、α和f三个对称边带滤波组件变量的数据统计函数。而组合切片分析的应用不仅有效地减少了滤波组件变量的组合次数，使得分析计算效率较高，而且切片分析算法对噪声不敏感，在低信噪比和早期轴承微弱故障检测中具有较大优势。算法的大致流程如下：

图3　基于MID算法的组合切片分析流程图 Fig.3 Flow chart of MID combination slice analysis

(1) 根据测量的轴承转速V，确定轴承轴频fr、保持架转频fb和典型故障理论特征频率值αtwai、αtnei、αtgun。

(2) 根据转速波动ΔV确定轴频和保持架转频的波动范围fr+Δr、fb+Δb。

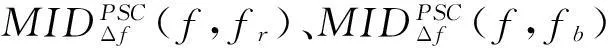
(4)找到频率波动范围内的局部最大能量切片，得到对应的实际轴频far和保持架转频fab。

(5) 通过far、fab得到实际转速Va, 直接确定典型外圈故障特征频率αawai、内圈故障特征频率αanei和滚动体故障特征频率αagun的实际值。

(7) 将上一步骤单切片组合的分析图谱和理论特征频率的对比，结合典型故障频谱结构特点，判断信号是否存在故障，及其具体故障类型。

3仿真分析

假设振动信号包含单一载波频率，则滚动轴承振动中的等间隔冲击脉冲调制信号可以描述为：

s(t)=Ae-ξωrt sin(ωrt)u(t)

(4)

其中:A为冲击脉冲的幅值，ξ为阻尼特征常数，ωr为系统共振频率，u(t)为单位阶跃函数，n(t) 为白噪声。脉冲调制振动信号为：

(5)

其中：fr为信号的故障特征频率，τi为滚珠和滚道之间微小滑动对故障特频率的影响因子。仿真信号取A=1,ωr=2*pi*1000,fr=60,τi为0.01/fr～0.02/fr之间的随机数。采样频率为25600Hz,n(t)为白噪声，信号的信噪比为-15dB。图4(a)- (f)分别对应于二阶调制信号的输出图谱。

从仿真信号频谱结构可以看出信号的主要频率集中在1000 Hz左右，因而包络解调分析的中心频率选为1 000 Hz，带宽为400，得到包络解调输出结果4(c)。与直接MID输出结果相比较可以看出，包络解调方法提取的故障特征频率与噪声成分混叠，能够说明出现了故障，但是故障特征不明显，主频幅值仅为0.094 mV并且能够提取出来的最高倍频成分为3阶。其原因是在噪声较大的情况下，包络解调方法只选择了信号的共振频带，削弱了故障成分并且解调分析不能有要避免加性噪声成分的干扰。三维切片分析图4(e)能够清晰地显示故障特征频率的前3阶成分对应的MID组合切片，由切片分析的流程图3可知实际转速对应实际的故障特征频率对应确定的单一切片，这样可以增强诊断的准确性，降低了噪声的影响，有效地减少了计算量。结合图5可以看出切片分析输出故障特征频率幅值并不随信号SNR变动，说明该方法非常适应于低信噪比、早期微弱故障特征的提取。

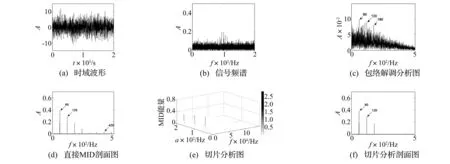
图4　二阶仿真信号分析结果 Fig.4 Analysis results of a simulated second-order signal

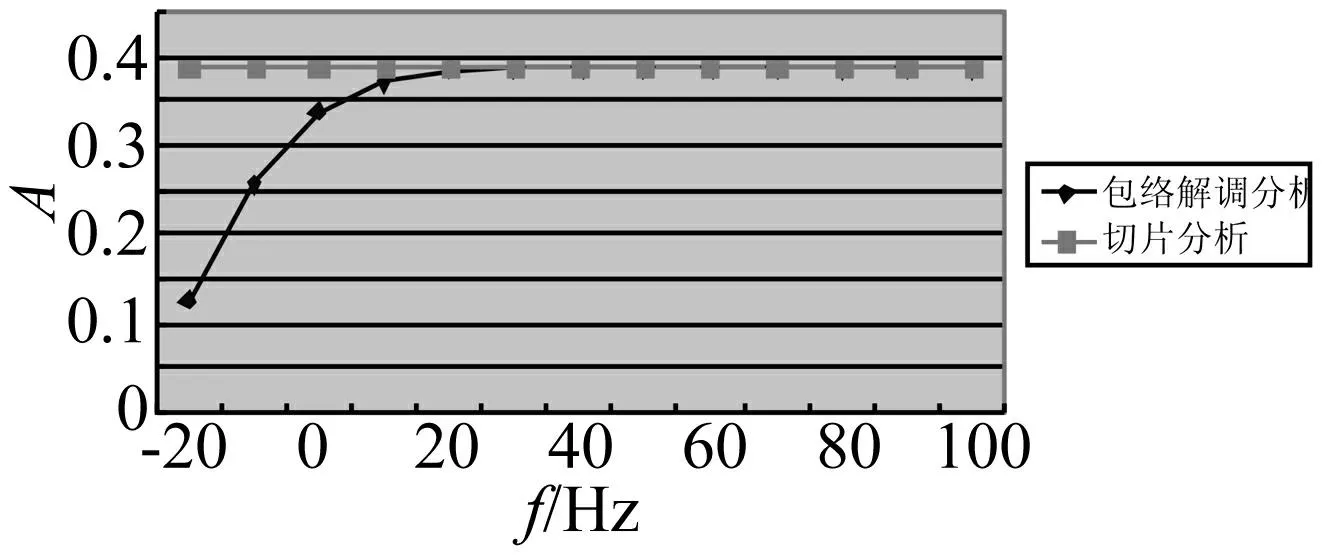
图5　包络解调分析和切片分析的主频幅值对比图 Fig.5 Comparison of main frequency amplitude between Envelope analysis and MID slices analysis

为了验证算法在低信噪比情况下提取故障的能力，首先变动轴频，用y=1 000+awgn(ωr,SNR)替换仿真信号中的载波；然后变动随机噪声，用y=1 000+awgn(x,SNR)替换仿真信号,式中SNR取值范围为-10～100 dB，步长为10;通过仿真实验得到统计分析图6。可以看到在轴频变动较大和背景噪声较强时，提取出来的故障特征频率幅值较小，当信噪比大于5 dB以后，故障特征频率的幅值就基本恒定，有效地证实了MID组合切片分析对噪声不敏感的优点。

图6　输入二阶调制信号SNR和 输出故障特征频率幅值关系图 Fig.6 Relationship between main frequency amplitude in output signal and SNR in input one

4实验验证

为了说明MID切片分析方法的实用性，采用如图7所示的QPZZ-Ⅱ旋转机械振动及故障模拟实验平台进行数据实测。信号的采样频率为25600Hz，轴承转速为314r/min。根据滚动轴承的参数得到理论故障特征频率分别为：轴频5.25Hz，保持架转频2.11 Hz，外圈故障特征频率27.47Hz，内圈故障特征频率40.64Hz，滚动体故障特征频率25.9Hz。

表1　滚动轴承N205EM基本参数

图7　QPZZ-Ⅱ机械故障模拟试验台 Fig.7 QPZZ-Ⅱ Fault simulation platform

作为对比，下文中对每组信号进行MID切片分析的同时，还进行了包络解调分析。根据轴承结构参数和故障特征，结合峭度相关理论，包络解调分析过程中的预处理带通滤波器通带范围选为[75008500]Hz。

图8(a)、图8(b)分别表示轴承振动信号的时域波形和信号频谱。微弱的有用信号时常淹没在噪声之中，但从时域波形8(a)上可以看出，信号中夹杂着周期性的冲击脉冲响应信号，其二阶统计量表现出循环平稳特征。在切片剖面图8(f)中，故障特征频率27.9Hz及其谐波处的切片具有显著的能量分布，其余切片上几乎不存在能量分布。

从信号的包络解调分析图8(c)可以看出除故障特征频率以外还存在其它强背景噪声干扰成分，干扰过大就会引起误诊断而不能提取故障。而直接MID剖面图8(d)不仅克服了噪声的影响，而且凸显了故障特征,主频幅值能达到2.35mV。图8(f)则在直接MID基础上做切片分析处理，有效降低了运算量。

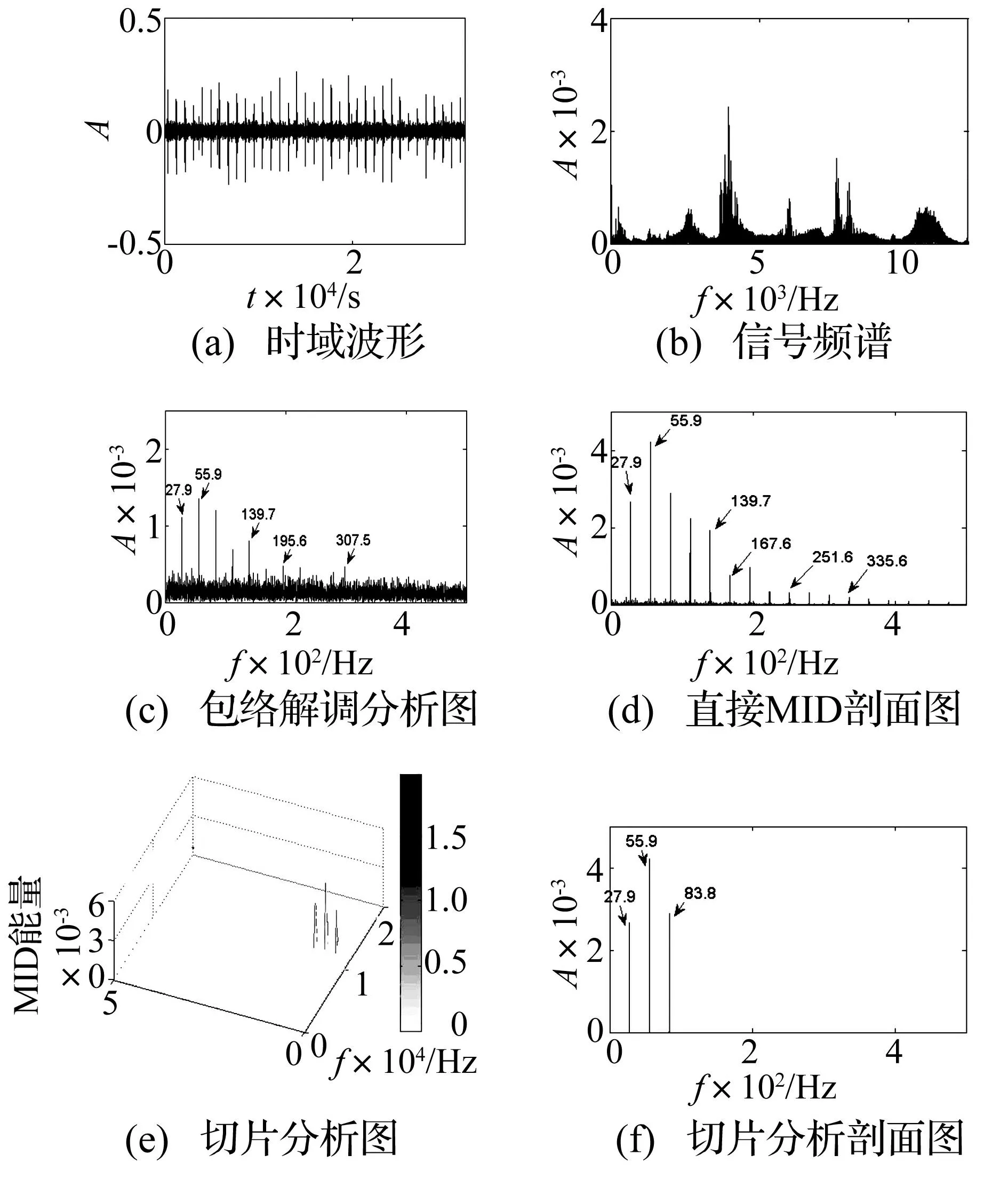
图8　外圈故障信号分析结果 Fig.8 Analysis results of outer race fault

图9(a)～图9(f)分别表示信号的时域波形、信号频谱、包络解调分析图、直接MID剖面图、组合切片分析和切片分析剖面图。内圈剥落部位与滚动体接触位置的变化，使得内圈剥离引起的冲击受到较强的轴频调制作用。通过转速波动范围可以计算出轴频调制密度(MID)切片带，然后通过能量最大轴频切片带得出信号的实际轴频为5.3Hz，初步判定信号具有内圈故障特征。根据实际轴频确定典型故障特征频率并计算相应的单切片，从图9(f)可以看出信号只在37.4Hz及谐波切片能量突出，故判定轴承发生内圈剥离故障。

而从包络解调分析图9(c)中可以看到，虽然信号中存在轴频成分5.3Hz和故障特征频率37.4Hz的峰值，但主频幅值仅为0.75mV，故障特征不明显。直接MID能够提取出突出的故障特征，主频37.4的幅值能达到1.79mV，谐波次数达到10阶。而且在进一步的MID切片分析通过预判轴频，确定实际的故障特征频率的频带范围，计算的MID切片不仅削弱了噪声的影响，而且减少了计算量，满足了工业实时性的要求。

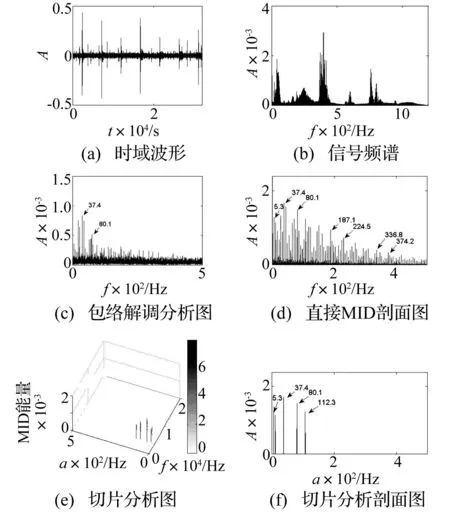
图9　内圈故障信号分析结果 Fig.9 Analysis results of inner race fault

图10(a)～图10(f)分别为滚动体剥离故障的相应输出图谱。滚动体剥落区与内外滚道发生接触位置和接触力的变化，使得滚动体剥离引起的冲击受到较强的保持架转频调制作用。从MID组合切片分析图10(f)可以看出 ，2.1 Hz和26 Hz及谐波切片能量突出，分别对应于保持架转频和滚动体故障特征频率的理论值,说明轴承发生了滚动体剥离故障。

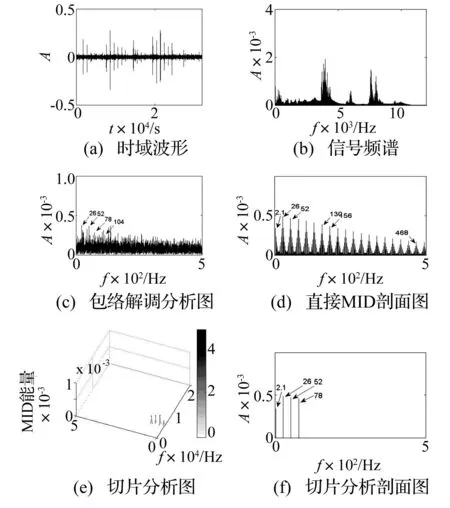
图10　滚动体剥离信号分析结果 Fig.10 Analysis results of roller element stripping

从包络解调分析图10(c)可以看到故障特征频率的4倍频，但是故障特征并不明显，频谱不能显现内圈故障冲击和保持架转频的调制特征。直接MID输出故障特征频率主频的幅值达0.48 mV,谐波次数达到18阶以上，该方式能够很好地显示调制特征，突出故障特征。而MID切片分析通过预判保持架转频，确定故障特征频率的频带范围，计算前3次谐波频带的MID且切片来判定滚动体故障的存在。

5结论

相对包络解调分析，MID切片分析不需要选择共振频带并且受轴承振动信号噪声影响小；相对ICC和IMID方法，MID切片分析方法只选择轴频、保持架转频、外圈典型故障特征频率、内圈典型故障特征频率和滚动体剥离故障特征频率变动的频带作为MID算法的计算切片带，而且可以通过轴频和保持架转频切片带的计算来预判故障类型，从而确定更为准确的典型故障单切片，有效的减少了计算量，降低了输出谱的冗余性，满足了工业生产的实时性和可靠性要求。除在QPZZ-II系统的滚动轴承故障模拟实验平台对所提方法进行验证分析外，该方法还成功应用于装有352226X2-2RZ型滚动轴承的铁路货车，成功地提取出各类典型故障。然而不是所有的故障类型都能通过几何结构计算出其理论变动的频带的，所用方法在适应非典型故障情况下还需进一步改进和完善。

参考文献

[1]李云，郭瑜，那靖，等.基于包络同步平均的齿轮故障诊断[J].振动与冲击，2013,32(19)：17-21.

LI Yun, GUO Yu, NA Jing, et al. Gear fault diagnosis based on envelope synchronous average[J]. Journal of Vibration and Shock,2013,32(19)：17-21.

[2]Randall R B,Antoni J, Chobsaard S. The relationship between spectral correlation and envelop analysis in the diagnostics of bearing faults and other cyclostationary machine signals[J]. Mechanical Systems and Signal Processing, 2001, 15(5):945-962.

[3]Antonidais I, Glossiotis G. Cyclostationary analysis of rolling-element bearing vibration signals[J]. Journal of Sound and Vibration,2001,248 (5) :829-845.

[4]李力,屈梁生. 循环统计量方法在滚动轴承故障诊断中的应用[J]. 振动、测试与诊断, 2003, 23(2): 116-119.

LI Li, QU Liang-sheng.Application of cyclic statistics to fault diagnosis of rolling bearings[J]. Journal of Vibration,Measurement & Diagnosis,2003, 23(2): 116-119.

[5]Urbanek J, Antoni J. Barszcz T. Detection of signal component modulations using modulation intensity distribution[J]. Mechanical Systems and Signal Processing,2012, 28:399-413.

[6]Antoni J. Cyclic spectral analysis of rolling-element bearing signals: facts and fictions[J]. Journal of Sound and Vibration,2007, 304 (3-5) : 497-529.

[7]Urbanek J, Antoni J, Barszcz T. Integrated modulation intensity distribution as a practical tool for condition monitoring[J]. Applied Acoustics, 2014,77 :184-194.

[8]毕果，陈进.组合切片分析在滚动轴承故障诊断中的研究[J].机械科学与技术，2009,28(2)：182-186.

BI Guo, CHEN Jin. The application of combination slice analysis of spectral correlation density in rolling element bearing diagnosis[J].Mechanical Science and Technology for Aerospace Engineering, 2009,28(2)：182-186.

[9]Ming A B,Qin Z Y,Zhang W, et al. Spectrumauto-correlation analysis and its application to fault diagnosis of rolling element bearings[J]. Mechanical Systems and Signal Processing,2013,41:141-154.

[10]王宏超，陈进，董广明，等.基于快速Kurtogram算法的共振解调方法在滚动轴承故障特诊提取中的应用[J].振动与冲击，2013,32(1)：35-37.

WANG Hong-chao,CHEN Jin,DONG Guang-ming, et al. Application of resonance demodulation in rolling bearing fault feature extraction based on fast computation of Kurtogram[J]. Journal of Vibration and Shock,2013, 32(1):35-37.

[11]Zimroz R， Bartelmus W.Urbanek B, et al. Diagnostics of bearings in presence of strong operating conditions non-stationarity-A procedure of load-dependent features processing with application to wind turbine bearings[J].Mechanical Systems and Signal Processing,2014, 46:16-27.