加工中心双直线电机自适应模糊滑模同步控制*

于冬梅，刘 丹，胡 庆

(沈阳工业大学 电气工程学院功率电子与运动控制研究所，沈阳 110870)

0 引言

移动龙门加工中心的主机结构为龙门框移动、工作台固定式的结构。这种结构需要安装在X 轴的两台永磁同步直线电机(PMLSM)协调地同时推动龙门移动。X 轴采用双直线电机驱动，可以使龙门达到较高的功率密度，并且当两台电机适当的协调及同步运动时，没有显著横向的偏移［1］。当两个子系统的控制器参数相同及被控对象参数不变的情况下，两个伺服系统的输出也是相同的。但是在机床实际运行过程中，刀架移动导致直线电机承载的动子质量的变化和端部效应以及负载的动态变化都会造成两个子系统的位置输出不同步。针对双直线电机的位置同步控制问题，文献［2－7］等已经做了大量的研究，尤其是智能控制方法的引入，较大程度的提高了同步控制的性能。但是单独采用模糊控制时，稳态位置同步误差精度较低。因此在设计同步补偿控制器时，为提高同步控制精度，采用了自适应模糊滑模同步控制器，该同步补偿方法充分利用了滑模控制的快速响应及对被控对象变化不敏感的特性［8］。用模糊控制削弱滑模抖振的同时，设计了一个自适应调节律来估计最优的调节量，以较小的控制量达到了较好的跟踪性能，保证了系统的稳定性又易于工程实现。该方法继承了滑模控制的快速性，又克服了系统接近稳态时模糊控制不精确的弱点，为同步控制提供了一种快速精确的控制方法。

1 永磁直线同步电机数学模型

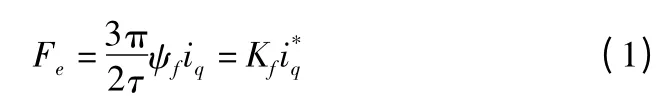
PMLSM 驱动系统的机械方程可以表示为:

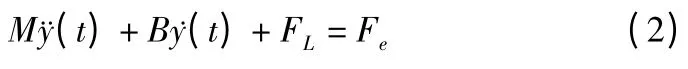
其中y 为动子的位置输出，M 为直线电动机动子质量，B 为粘滞摩擦系数，FL为负载阻力，Fe为电磁推力i*

q 是q 轴电流，Kf是推力系数，τ 为极距，ψf为永磁体的励磁磁链。把式(1)代入式(2)，可以得到PMLSM 的运动方程为:

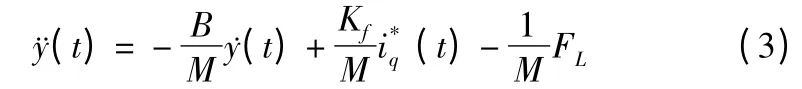
还可以写为:

在没有干扰和负载的情况下，PMLSM 标准模型可以表示为:

但是机床在实际运行时加工刀具在垂直X 轴方向移动会使X 轴方向上两个直线动子的质量M 发生变化，同时一些不确定的干扰及粘性摩擦系数B 也会发生变化，那么式(4)可以表示为:

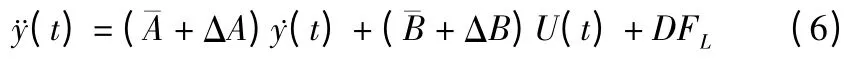
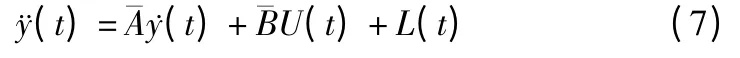
其中ΔA 和ΔB 表示系统参数M 和B 的变化量，定义L(t)为系统所受的扰动集合表示为:L(t)=ΔA(t)+ΔBU(t)+ DFL，并规定这些干扰是有界的，即|L(t)| ＜ρ，ρ 是正常数。

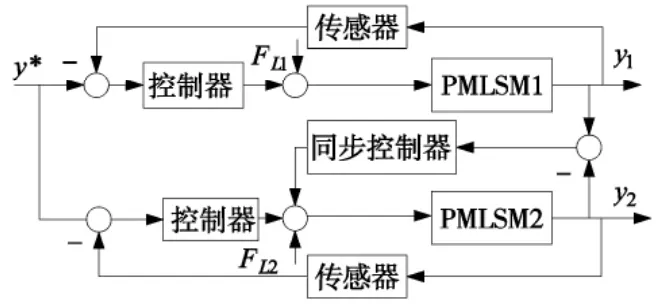
图1 双直线电机同步控制结构框图

2 双直线电机位置伺服同步控制系统

两直线电机采用并行控制方式和主从控制相结合的控制结构。将两个同方向进给轴，一个设定为主动轴，另一个设定为从动轴。每个轴分别由相同的CNC 控制单元、伺服驱动器、永磁直线同步电动机、位置和速度反馈装置组成伺服运动控制回路。对两台永磁直线同步电机给予相同的给定信号，两个位置和速度反馈信号除了送回各自的伺服驱动器比较外，将主从电机的位置和速度信号之差作为同步控制器的输入信号。这样既保证了给定信号的一致性，提高了主从控制中每个电机的伺服精度，又克服了并联控制中两个电机的自由运行状态。

单轴子系统的设计采用积分，比例控制器位置控制方法，位置调节器采用比例控制器，电流调节器采用比例积分控制器即PI 控制。在选择较高的积分增益KI时，对参考信号具有很快的响应能力及对负载扰动具有较强的抑制能力［9］。

图2 基于自适应模糊滑模的同步控制器设计框图

3 自适应模糊滑模控制器设计

对(8)进行微分:

定义二维的滑模面为:

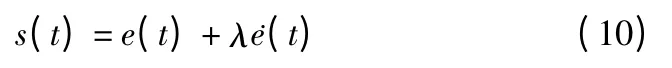
其中y1(t)和v1(t)是PMLSM1 的位移和速度信号，c是正常数。对上式进行求导，并由(7)可以得出:

当L(t)≠0 时，等效控制作用不能保证较好的控制效果。因此必须设计辅助控制来消除摄动的影响。

令滑模面s 作为模糊控制的输入变量，模糊集表示为{N(负)Z(零)P(正)}。U 为输出的语言变量，其模糊集可以表示为:{DU(减少)NU(标准)IU(增加)}。那么模糊滑模控制系统模糊语言规则描述如下:

(1)If s is P，then U is DU

(2)If s is Z，then U is NU

(3)If s is N，then U is IU

s 的模糊集的隶属度函数是三角函数，且w1+w2+w3=1。模糊滑模控制系统中采用三角型隶属度函数，中心解模糊法。DU、NU、和IU 隶属度函数

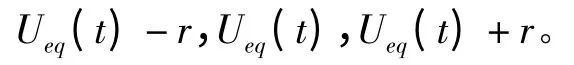
则控制量为:

其中，r ＞0 是调节量;0≤w1≤1，0≤w2≤1，0≤w3≤1是规则(1)－(3)的权重。所以:

选择Lyapunov 函数:

并对其进行微分:

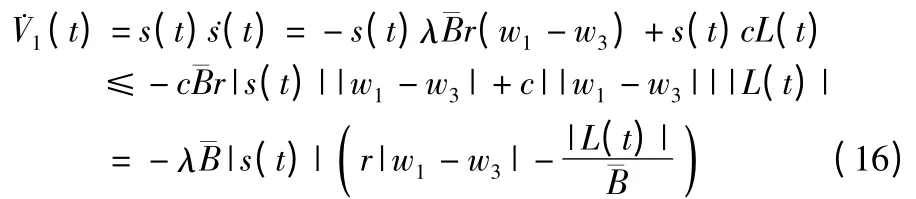
要满足滑模可达条件:

则必须:

成立。

由式(14)可以看出控制量的最大值是有调节量r 决定的，同时这个调节量的大小是由L(t)的幅值决定的，只有两者相等才能保证误差状态能够回到滑模面。如果调节量太小，那么跟踪误差的状态轨迹就会远离滑模面。因此比较保守的做法是要尽量取较大的r 值。但是如果r 值过大，就要产生过大的控制作用，这在实际应用当中是很难实现的。为了克服这个缺点，设计一个自适应调节律来估计最优的调节量，以较小的控制量保证较好的跟踪性能。由式(17)，定义最优的调节量r*，以实现最小的控制作用并满足滑模条件。

其中ε 是一个很小的正常数。在实际应用当中对应不确定因素的影响，最优的调节量r*是很难获得的。因此决定采用简单的自适应律来估计调节量的最优值。

定义调节量的估计误差为:

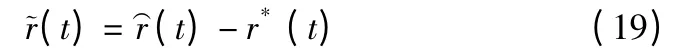
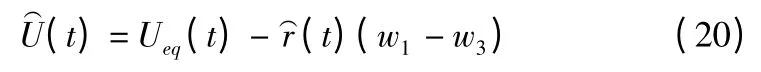
选择Lyapunov 函数:

其中α 是一个正常数，对上式进行微分得到:

将(11)、(12)、(18)(20)代入(22):

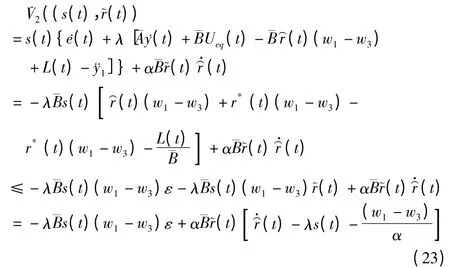
可以定义r 的自适应率为:

那么(17)可以变为:

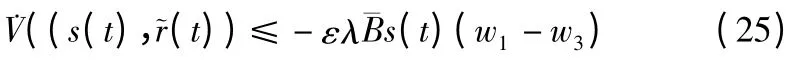
根据不等式s(t)(w1－w3)≥0，可以满足((s(t)，～r(t))≤0，所以((s(t)，～r(t))是半负定的。以上分析可以证明尽管有不确定干扰发生时自适应模糊滑模控制系统也是稳定的，同时跟踪误差e(t)会随着s(t)→0 而趋于零。

4 系统仿真

本文使用MATLAB 对提出的方法进行验证。仿真中选用的永磁直线同步电机的参数如下:M =5.8kg，B=2N·s/m，Kf=10.97N/A。根据系统框图和公式，利用Simulink 模块进行仿真。两个伺服系统采用相同的阶跃输入信号，并给PMLSM 施加随机干扰，仿真结果如图3 ～图6。其中图3 为随机扰动作用下两个单轴位置输出曲线。为了清晰的展现同步控制效果，图4 为图3 的结果放大图。图5 和图6分别为随机扰动下自适应模糊滑模同步控制和模糊滑模同步控制的两个直线电机的位置误差响应曲线，可以看出自适应模糊滑模控制作用下的最大位置误差为10.0μm，模糊滑模同步控制作用下的最大位置误差为20.0μm。有比较结果可以看出，采用自适应模糊滑模变结构控制的补偿效果明显优于模糊滑模控制，提高了位置同步精度。

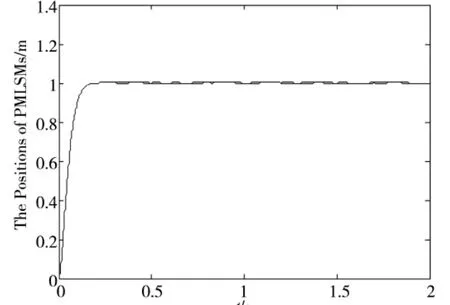
图3 阶跃信号输入下双直线电机位置响应曲线

图4 阶跃信号输入下双直线电机位置响应曲线

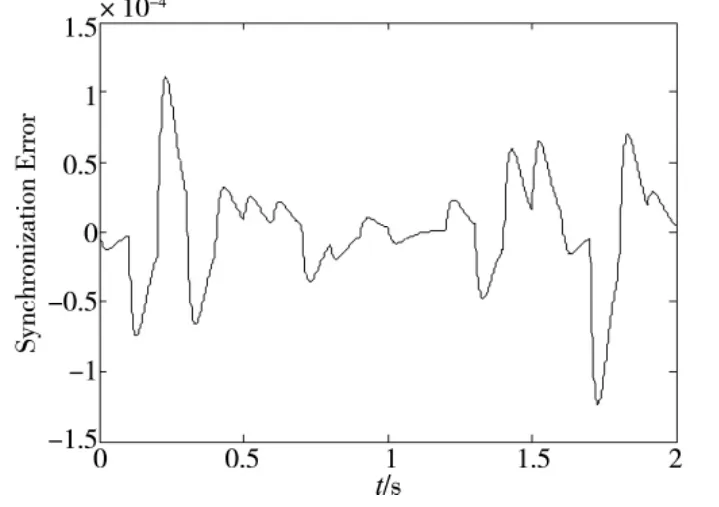
图5 双直线电机自适应模糊滑模同步控制位置同步误差

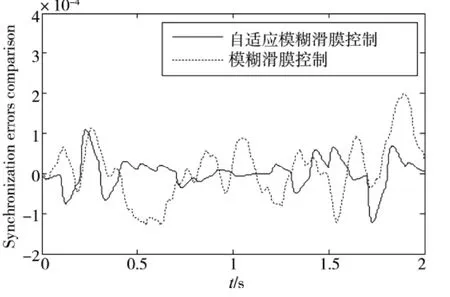
图6 双直线电机模糊滑模同步控制位置同步误差曲线

5 结论

本文将自适应模糊滑模控制应用于双直线电机驱动的龙门移动式加工中心，设计了自适应模糊滑模同步控制器。同步控制系统的数学模型简单，控制器运算不算复杂，仿真结果验证了该方法的可行性，同步控制的精度得到了明显提高。

［1］Teo，C. S，Tan，K. K，Huang，S and Lim，S. Y，(2005).Dynamic Modeling and Adaptive Control of a Multi-Axial Gantry Stage Source:IEEE The International Conference on System4，3374－9.

［2］S-L Chen1，W-M Lin1，and T-H Chang. Tracking control for a synchronized dual parallel linear motor machine tool.Systems and Control Engineering. Proc. IMechE Vol. 222 Part I.2008.

［3］黄元峰，王海峰. 基于滑模变结构控制算法的无刷直流电机力矩平衡控制系统研究［J］. 电机与控制应用，2012，39(2):9－11.

［4］唐光谱，郭庆鼎，张凤，等. 同步传动技术在龙门移动式镗铣床中的应用［J］. 沈阳工业大学学报，2002，4(2):57－59.

［5］唐光谱，郭庆鼎. 基于H∞鲁棒控制器的高精度快速同步进给技术的应用研究［J］. 电机与控制学报，2001，9(3):175－178.

［6］翁秀华，郭庆鼎.刘德君. 双直线电机同步驱动系统中模糊自适应PID 控制方法的研究［J］. 沈阳工业大学学报，2005，27(1):34－37.

［7］邢银龙. 数控加工中心龙门同步磁悬浮系统的控制研究［D］. 沈阳:沈阳工业大学，2012.

［8］刘金琨，孙富春. 滑模变结构控制理论及其算法研究与进展控制理论与应用［J］. 控制理论与应用，2007，24(3):407－418.

［9］郭庆鼎，王成元，周美文，等. 直线交流伺服系统的精密控制技术［M］. 北京:机械工业出版社，2001