一类具时滞的能源价格模型的稳定性与Hopf分支

殷红燕，刘晶晶,周 静

(中南民族大学 数学与统计学学院， 武汉 430074)

党的十八大报告指出：“推动能源生产和消费革命，控制能源消费总量，加强节能降耗，支持节能低碳产业和新能源、可再生能源发展，确保国家能源安全．”能源问题引起我国政府的重视．而随着能源需求的高速增长，能源短缺的现象越来越剧烈，能源价格的持续增长影响着我国经济的平衡增长．国内外已有很多学者对能源价格与能源供需关系做了研究．在我国，田立新等一批学者首次将非线性混沌动力学理论引入能源经济系统，在能源供需和能源价格的建模与分析中取得了显著成果．其中文献[1]建立了能源价格的动态模型，通过对模型平衡点的稳定性分析，得出了均衡价格的稳定条件．考虑到现实的能源市场不可能每期都能达到市场出清，能源供需总处在不均衡状态，文献[2]建立了更能准确反映能源经济现实的能源价格与能源供需的非线性时滞微分方程模型，即：

μbP(t)-μaP(t-τ)+μ(d0-s0)，

(1)

其中参数μ>0，a>0，b>0，d0>0，s0≥0，α,β,γ是任意常数．

(2)

文献[2]给出了方程(1)的意义，并利用了主项分析法和Hopf分支理论对系统平衡点进行分析，给出了各种参数条件下能源价格的局部稳定性条件和出现Hopf分支的条件，得出能源经济系统的相关条件．本文以时滞τ为参数，利用Hassard等在文献[3]中所介绍的规范型方法，讨论系统(2)的稳定性以及Hopf分支的存在性以及分支方向、分支周期解的稳定性.

1 平衡点的全时滞稳定性

为了讨论问题方便，给出如下已有的结论.

引理1[4]具有时滞的常系数线性系统

其零解全时滞稳定的充要条件为：

(i) 其特征方程Δ(λ,τ)=0，当τ=0时所有根具有负实部．

(ii) 对∀y,τ∈R,τ>0，均有Δ(iy,τ)≠0．

(3)

系统(3)的特征方程为：

λ2+Aλ+B+Ce-λτ=0,

(4)

当τ=0，方程(4)变为：

λ2+Aλ+B+C=0，

(5)

当τ≠0时，若λ=iω(ω>0)是特征方程(4)的一个根当且仅当ω满足：

(6)

对方程组(6)的两个方程分别平方再相加得：

ω4+(A2-2B)ω2+B2-C2=0,

(7)

方程(7)的根为：

由上讨论，应用引理1，可得如下定理1.

定理1 系统(2)的平衡点全时滞稳定的充要条件是：

2 Hopf分支的存在性

(8)

显然当τ=τj时，λ=±iω0是方程(4)的一对共轭纯虚根．

3 分支方向及分支周期解的稳定性

(9)

对φ∈(φ1,φ2)T∈C[-1,0]=C([-1,0],R2)，定义一个算子:

Lσφ=Dφ(0)+Eφ(-1),

其中:

且定义：

f(σ,φ)=

对φ∈(φ1,φ2)T∈C1[-1,0]，定义：

和:

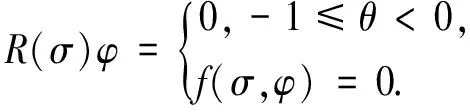
于是可把方程(9)写成如下形式[7]：

(10)

对于φ∈C[-1,0]，Ψ∈C1[0,1]，定义双线性积

其中η(θ)=η(θ,0)，则算子A=A(0)与A*是共轭算子，而±iτ0ω0是算子A(0)的特征值，且其它特征值具有严格负实部，从而±iτ0ω0也是算子A*的特征值，于是经过计算可得到下面的结论.

下面计算中心流形C0在σ=0时的坐标，令Ut是方程(10)在σ=0时的解，定义：

z(t)=〈q*,Ut〉,W(t,θ)=Ut(θ)-2Rez(t)q(θ).

(11)

既然σ=0时，解Ut∈C0，有：

再把上式改写成：

其中：

由(11)式有：

注意到q(θ)=(1,iω0)Teiω0τ0θ，所以可得：

因此：

下面计算W20(θ)和W11(θ)，根据(10)和(11)式有：

其中：

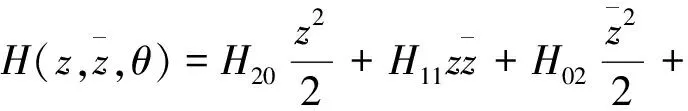
当θ∈[0,1)，可以得到：

(A-2iω0τ0)W20(θ)=-H20(θ),

AW11(θ)=-H11(θ)．

(12)

经计算可知：

其中E1，E2的值可由θ=0时H的值来确定．由A的定义和(12)式，利用文[3]或文[8]中的方法，可解得E1=(A1,A2)T，其中：

A2=2iω0A1.

E2=(B1,B2)T，

更进一步，我们可以求出g21，那么gij完全可以由系统(9)的系数表示出了，于是通过计算得到：

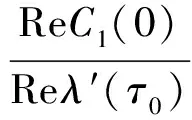
定理3 对方程(9)，分支周期解的分支方向由μ2决定：如果μ2>0(或μ2<0)，则Hopf分支为上临界(或下临界)；分支周期解的稳定性由β2决定：当β2<0(或β2>0)时，分支周期解是稳定的(或不稳定的)；分支周期解的周期由T2决定：如果T2>0(或T2<0)，周期解是增加的(或减少的)．

[1] 邓祥周，田立新，段希波. 能源价格的动态模型及分析[J]. 统计与决策，2007,36(2):9-10.

[2] 田立新，钱和平．能源价格时滞微分方程模型及动力学分析[J]．江苏大学学报：自然科学版，2010，24(2)：240-244．

[3] Hassard B，Kazarinoff D，Wan Y H．Theory and applications of Hopf bifurcation [M].London: Cambridge University Press，1981:181-191.

[4] 秦元勋，刘永清，王 联. 带有时滞的动力系统的运动稳定性[M].北京:科学出版社,1963:51-52.

[5] 田晓红，徐 瑞. 一类具时滞和阶段结构的捕食模型的稳定性和Hopf分支[J].高校应用数学学报A辑,2010,25(3):285-291.

[6] Cooke K,Grossman Z. Discrete delay,distributed delay and stability switches[J]. J Math Anal Appl,1982,86:592-627.

[7] Hale J K.Theory of functional differential equations[M].Berlin：Springer-Verlag,1977:112-159.

[8] 魏俊杰，王洪滨，蒋卫华. 时滞微分方程的分支理论及应用[M].北京:科学出版社,2012:61-67.