直觉判断矩阵的直觉模糊数型权重研究

涂振坤，刘心报

(1.合肥工业大学管理学院,安徽合肥 230009;2.合肥工业大学数学学院，安徽合肥 230009)

直觉判断矩阵的直觉模糊数型权重研究

涂振坤1，2，刘心报1

(1.合肥工业大学管理学院,安徽合肥 230009;2.合肥工业大学数学学院，安徽合肥 230009)

研究了确定直觉判断矩阵的权重问题,并对与权重的可靠性密切相关的直觉判断矩阵的一致性问题进行了探讨.从直觉模糊数的得分函数和精确度函数角度给出直觉判断矩阵的加型一致性的新定义,并导出加型一致性的等价条件.为了充分利用原直觉判断矩阵的信息以及使决策符合一致性要求,根据加型一致性的等价条件运用转换函数将原直觉判断矩转换为两个加型模糊一致性互补判断矩阵,然后对这两个加型模糊一致性互补判断矩阵运用行和归一的方法分别求出原直觉判断矩阵权重的隶属度和非隶属度,从而得到直觉模糊数型权重,并利用直觉模糊数的排序方法进行排序.最后讨论了决策方法的优良性质,并通过实例验证了决策方法的有效性和实用性.

直觉判断矩阵;直觉模糊数型权重;中转法;一致性

0 引言

1965年Zadeh[1]针对事物的不确定性提出了模糊集理论.隶属函数值只能是单一值,传统的模糊集理论不能完整表达问题的全部信息而受到制约和挑战[2].Atanassov[3-4]提出同时考虑隶属度、非隶属度、犹豫度这3个方面信息来描述客观世界的模糊性,提出了直觉模糊集理论.

在决策过程中,决策者往往不能直接给出属性的权重,而是对属性进行两两比较并构造判断矩阵,然后按照一定的方法求得权重.关于确定实数型的判断矩阵(互反判断矩阵、模糊互补判断矩阵等)权重的研究已经比较成熟.由于决策者给出的判断矩阵是否满足人类决策思维的一致性影响到所得权重的可靠性,因此人们往往将判断矩阵满足一定的一致性作为确定权重的前提条件.Satty[5]研究了互反判断矩阵的一致性和可接受一致性.Tanino[6]给出了模糊互补判断矩阵的有限制的极大-极小传递性、有限制的极大-极大传递性、加型传递性以及积型传递性的定义.随后人们根据这些一致性提出了大量有关模糊互补判断矩阵的排序方法[7-10]. Xu[7]对原始模糊互补判断矩阵进行数学变换得到加型模糊一致性互补判断矩阵,然后利用加型模糊一致性互补判断矩阵的特点求得原模糊互补判断矩阵的排序向量.Xu[8]用排序的权值构造加型模糊一致性互补判断矩阵来逼近实际模糊互补判断矩阵,从而给出模糊互补判断矩阵排序的一种最小方差法.Xu[9]将积型模糊一致性互补判断矩阵转化为一致性互反矩阵,再利用一致性互反判断矩阵的特征向量法求出排序向量,即得到原判断矩阵的权重.Xu[10]用排序的权值构造积型模糊一致性互补判断矩阵来逼近实际模糊互补判断矩阵,从而给出模糊互补判断矩阵排序的一种最小偏差法.这些排序方法对于研究非实数型判断矩阵的权重问题有着重要的启发意义.

近年来,关于非实数型的判断矩阵(如区间互反判断矩阵、区间互补判断矩阵、直觉判断矩阵等)权重问题的研究也取得了一些进展.本文研究的是直觉判断矩阵的权重确定问题,而文献[2,11-12]指出直觉判断矩阵等价于区间互补判断矩阵,因此下面介绍区间互补判断矩阵与直觉判断矩阵权重确定方法的已有研究成果[13-31].Xu[13]对区间互补判断矩阵进行行和归一化求得区间数型权重,并利用区间数比较的可能度矩阵得到了判断矩阵的排序向量.Xu[14]利用均值互补判断矩阵的排序向量以及随机误差公式求出原矩阵的区间数型权重,用可能度矩阵得到了实数型排序向量.Gong[15]利用一致性区间互反判断矩阵的排序向量得到一致性区间互补判断矩阵的区间数型权重向量,并运用偏差的思想建立了非线性规划模型，求得一般情况下区间互补判断矩阵的区间数型权重向量.Liu[16]运用凸组合方法将区间互补判断矩阵转化为一族实模糊互补判断矩阵,在后者满足弱传递性情况下,将这族矩阵的可靠权重集成为区间数型权重.Liu[19]给出了区间互补判断矩阵与区间互反判断矩阵的转换关系,基于可接受一致性区间互反判断矩阵的区间数型权重求解公式得到了可接受一致性区间互补判断矩阵的区间数型权重. Xu[20]定义了加型一致性区间互补判断矩阵的概念,在区间互补判断矩阵具有加型一致性情况下运用权重可行域的思想求得区间数型权重,并针对不一致的情况利用加型一致性区间互补判断矩阵逼近实际区间互补判断矩阵,并使得偏差最小化而得到线性规划模型,从而求得区间数型权重.Wang[21]在加型一致性互补判断矩阵等价条件的基础上给出了加型一致性区间互补判断矩阵的新定义；并讨论了区间互补判断矩阵在具有加型一致性情况下运用权重可行域是区间的思想建立了线性规划模型以求得区间数型权重；而在不一致的情况下构造加型一致性区间互补判断矩阵逼近实际区间互补判断矩阵,将问题转化为求解构造得到的加型一致性区间互补判断矩阵的区间数型权重.Lan[22]将积型一致性区间互补判断矩阵转换为加型一致性区间互补判断矩阵,并集成后者的加型一致性信息后再转换为积型一致性信息,最后设计算法得到积型一致性区间互补判断矩阵权重.Wang[23]基于正区间数的运算规则给出区间互补判断矩阵具有加型一致性、积型一致性及弱传递性的新定义,并构造出区间互补判断矩阵与其权重之间关系的转换函数. 而且在特定转换函数情况下,发现用权重得到的区间互补判断矩阵具有加型一致性、积型一致性,并且用它们逼近实际区间互补判断矩阵从而得到目标规划模型以求解区间数型权重向量.文献[25-31]讨论了直觉模糊环境下多属性决策问题.Li[25]利用线性规划模型得到属性的实数型权重,并采用TOPSIS思想给出决策方法.Xu[26]针对属性值为直觉模糊数且决策者对决策方案的偏好为直觉判断矩阵的多属性决策问题,分别利用所有方案的综合得分值构造出加型一致性与积型一致性互补判断矩阵,根据它们与决策者的直觉判断矩阵是否吻合建立相应的线性规划模型,求解属性的区间数型权重.Chen[27]运用多种得分函数计算备选方案与正理想点和负理想点的分离度,从而得到相应的贴近度,同时将考虑权重偏差最小化和贴近度加权和最大化的多目标问题转化为单目标的问题,并建立模型求得属性的最优权重及各方案的贴近度.Gong[28]利用直觉判断矩阵与区间互补判断矩阵的转换关系及区间互补判断矩阵的积型一致性的概念给出由权重表述的积型一致性直觉判断矩阵的定义；并针对个体和群体的情况,根据偏差的思想分别建立了目标规划模型以求得直觉判断矩阵权重. Xu[30-31]在属性权重未知条件下,基于信息理论和直觉模糊数(区间直觉模糊数)的相离度的概念,运用权重向量的选择应使得所有属性对所有方案的总偏差最大的思想建立了线性规划模型以求得个体直觉判断矩阵(区间直觉判断矩阵)的实数型权重向量.从以上文献可以看出确定区间互补判断矩阵(直觉判断矩阵)的权重方法主要可以分为以下几类方法.第一类是直接建立权重向量与判断矩阵元素之间关系的方法.首先在区间互补判断矩阵(直觉判断矩阵)是加型(积型)一致的条件下,分析出权重向量与判断矩阵元素之间的关系,即权重向量应满足的条件.然后根据决策者给出的矩阵不一定满足一致性,所以权重向量与判断矩阵元素之间的这种关系看成近似关系,即它们之间存在偏差.根据偏差最小化思想,建立模型以求出权重向量. 第二类是利用转换关系的方法.例如运用凸组合方法将区间互补判断矩阵转化为一族实模糊互补判断矩阵,然后将这族矩阵的可靠权重集成为区间数型权重.

虽然人们对于直觉判断矩阵(区间互补判断矩阵)的权重研究取得了一定的进展,但是还存在以下两个方面的问题:第一,虽然研究者给出了种种直觉判断矩阵(区间互补判断矩阵)的加型(积型)一致性的新定义[20-21,23,26,28-29],但是缺乏直接从直觉模糊数的角度给出定义的研究.第二,已有的研究大多数给出的权重的表达方式是区间数并利用区间数比较大小方法给出排序结果,但是缺乏直接将直觉模糊数作为权重的表达方式并利用直觉模糊数比较大小方法给出排序的研究.本文从直觉模糊数的得分函数和精确度函数角度给出直觉判断矩阵的加型一致性的新定义,并导出加型一致性的等价条件,然后根据加型一致性的等价条件运用中转的方法得到原矩阵的直觉模糊数型权重,并利用直觉模糊数的排序方法进行排序.最后讨论了决策方法的优良性质,并通过实例验证了决策方法的有效性和实用性.

1 基本概念

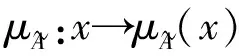
定义1.2[6,11]设Y={y1,y2,…,yn}为方案集,决策者对n个方案进行比较得到判断矩阵B=(bij)n×n,其中,bij表示决策者对方案yi和yj进行比较时偏爱yi的程度, 若B满足:

0≤bij≤1,bij+bji=1,i,j=1,2,…,n,

称B为模糊互补判断矩阵.

定义1.3[6,32]设B=(bij)n×n为模糊互补判断矩阵,若对任意i,j,k=1,2,…,n,qik≥0.5,qkj≥0.5,有qij≥0.5, 则称B满足传递性.

定义1.4[6,32]设B=(bij)n×n为模糊互补判断矩阵,若B满足:

(bik-0.5)+(bkj-0.5)=(bij-0.5)，

i,j,k=1,2,…,n,

称B满足加型一致性.

显然,由定义可知B若满足加型一致性则必然满足传递性.

定义1.5[4,2,33]设X是一个非空集合,称A={〈x,uA(x),vA(x)〉|x∈X}为直觉模糊集,其中，uA和vA分别表示X中元素x属于X的隶属度和非隶属度,且∀x∈X,有0≤uA(x)+vA(x)≤1.

根据直觉模糊集的定义,直觉模糊集的基本组成部分为元素x属于X的隶属度和非隶属度组成的序对,称之为直觉模糊数. 直觉模糊数一般记为α=(uα,vα),其中,0≤uα+vα≤1.

定义1.6[2,33]设直觉模糊数为α=(uα,vα),称s(α)=uα-vα为α的得分,称h(α)=uα+vα为α的精确度. 得分函数出发点是:隶属度比非隶属度具有越多的优势,越满足决策者要求.而精确度函数出发点是:确定的信息越多,越满足决策者要求.

关于直觉模糊数的排序方法很多,主要介绍以下方法:

定义1.7[2,33]设α1=(uα1,vα1),α2=(uα2,vα2)为直觉模糊数,若s(α1)h(α2),称α1大于α2,记为α1>α2.

定义1.8[2,33]设Y={y1,y2,…,yn}为方案集,决策者对n个方案进行比较得到判断矩阵Q=(qij)n×n,其中,qij=(uij,vij), 0≤uij≤1,0≤vij≤1,i,j=1,2,…,n.uij表示决策者对方案yi和yj进行比较时偏爱yi的程度,vij表示决策者对方案yi和yj进行比较时偏爱yj的程度, 1-uij-vij表示决策者对方案yi和yj进行比较时犹豫的程度,若uij∈[0,1],vij∈[0,1],uij+vij≤1,uij=vji,vij=uji,uii=vii=0.5，i,j=1,2,…,n,称Q为直觉判断矩阵.

定义1.9[2,33]设Q=(qij)n×n为直觉判断矩阵,若对任意的i,j,k=1,2,…,n,当qik≥(0.5,0.5),qkj≥(0.5,0.5)时,必有qij≥(0.5,0.5),则称Q满足传递性.

2 直觉判断矩阵加型一致性的新定义及其等价条件

为了方便起见,首先对Chen和Tan定义的直觉模糊数的得分函数进行简单的变形.设直觉模糊数为α=(uα,vα),令

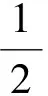
即

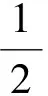
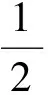
模糊互补判断矩阵B=(bij)n×n满足加型一致性的条件是

(bik-0.5)+(bkj-0.5)=(bij-0.5)，

i,j,k=1,2,…,n.

上式可以理解为:任意的i,j,k=1,2,…,n,决策者对方案yi和yk进行比较时yi的“得分”(bik-0.5)与对方案yk和yj进行比较时yk的“得分”(bkj-0.5)之和等于对方案yi和yj进行比较时yi的“得分”(bij-0.5).受此启发,我们认为决策者给出的直觉判断矩阵在得分方面满足加型传递性应该是加型一致性直觉判断矩阵的一个必要条件. 设Q=(qij)n×n,其中,qij=(uij,vij),i,j=1,2,…,n，则Q在得分方面满足加型传递性可以表示为

即

化简得

(1)

直觉判断矩阵不仅蕴含着直觉模糊数的得分信息，还包含有精确度方面的信息,因此,在精确度方面,直觉判断矩阵满足某种传递性也应该是加型一致性直觉判断矩阵的一个必要条件. 而加型一致性模糊互补判断矩阵B=(bij)n×n在精确度方面其实满足等式:

因此,我们要求直觉判断矩阵在精确度方面满足如下条件:

h((uik,vik))+h((ukj,vkj))=h((uij,vij))+1,

i,j,k=1,2,…,n.

即

(2)

提出加型一致性直觉判断矩阵要满足条件式(2)的原因在于两个方面:一方面是直觉判断矩阵在得分方面满足加型传递性启发我们认为其在精确度方面也要满足加型传递性; 另外一方面是我们找到的条件必须满足:当加型一致性直觉判断矩阵退化为加型一致性模糊互补判断矩阵时满足该条件.

下面我们分析式(2)的意义.从式(2)可以看出:当(uik+vik)增大, (ukj+vkj)也增大时,必有(uij+vij)也增大. 即当决策者对方案yi和yk进行比较时给出判断的精确度(uik+vik)增大, 并且对方案yk和yj进行比较时给出判断的精确度(ukj+vkj)也增大时,决策者对方案yi和yj进行比较时给出判断的精确度(uij+vij)也应增大. 同理,当(uik+vik)减小, (ukj+vkj)也减小时,必有(uij+vij)也减小.这与实际情况是相符合的.因此,式(2)利用加型一致性表示出了决策者在对方案两两比较给出判断时必须满足精确度(确定性的信息)方面的传递性.

因此,我们将同时满足条件(1)和(2)的直觉判断矩阵称之为加型一致性直觉判断矩阵.

定义2.1设直觉判断矩阵Q=(qij)n×n,其中,qij=(uij,vij),i,j=1,2,…,n，若Q满足:

(uik-vik)+(ukj-vkj)=(uij-vij),

(uik+vik)+(ukj+vkj)=(uij+vij)+1,

i,j,k=1,2,…,n,

则称为直觉判断矩阵Q满足加型一致性.

下面我们研究加型一致性直觉判断矩阵是否满足传递性.根据直觉模糊数的排序函数即定义1.7知:

(3)

由直觉判断矩阵Q满足加型一致性的定义和式(3)可以得到如下定理.

定理2.1设直觉判断矩阵Q=(qij)n×n,其中,qij=(uij,vij),i,j=1,2,…,n.若Q满足加型一致性,则Q满足传递性.

证明任意的i,j,k=1,2，…，n,当qik≥(0.5,0.5),qkj≥(0.5,0.5)时,下证qij≥(0.5,0.5).

若qik>(0.5,0.5),qkj≥(0.5,0.5),则uik-vik>0,ukj-vkj≥0.根据Q满足加型一致性, 故由式(1)知uij-vij>0,再由式(3)知qij≥(0.5,0.5).

同理可证: 若qik≥(0.5,0.5),qkj>(0.5,0.5),则qij≥(0.5,0.5).

若qik=(0.5,0.5),qkj=(0.5,0.5),则根据Q满足加型一致性, 故由式(1)知uij-vij=0,又由式(2)知uij+vij=1,因此,uij=vij=0.5.再由式(3)知qij≥(0.5,0.5).

□

下面我们对直觉判断矩阵的加型一致性定义做进一步的分析.

根据定义2.1,加型一致性直觉判断矩阵Q应满足方程组:

(4)

显然,上面的方程组等价于

于是我们得到如下结论:

定理2.2设直觉判断矩阵Q=(qij)n×n,其中,qij=(uij,vij),i,j=1,2,…,n,则Q满足加型一致性当且仅当Q满足如下方程组:

(5)

定理2.2给出了直觉判断矩阵Q满足加型一致性的等价条件.实际上,方程组(5)表示意义是:直觉判断矩阵Q的所有元素在隶属度和非隶属度方面均要满足加型传递性.

3 直觉判断矩阵排序的中转法及其性质

设决策者给出的直觉判断矩阵为Q=(qij)n×n,其中，qij=(uij,vij),i,j=1,2,…,n.为了方便起见,记U=(uij)n×n, 记V=(vij)n×n. 在现实决策过程中,由于主观和客观的原因,决策者给出的直觉判断矩阵Q往往不满足加型一致性,即往往不满足

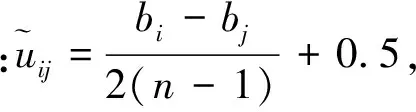
定理3.1直觉判断矩阵为Q=((uij,vij))n×n,通过中转法求得矩阵U=(uij)n×n和V=(vij)n×n的排序向量分别为{uj,j=1,2,…,n},{vj,j=1,2,…,n},则

i=1,2,…,n,

证明①

同理可得

i=1,2,…,n.

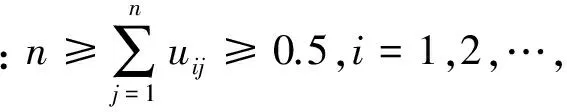
故ui>0,i=1,2,…,n.

同理可得vi>0,i=1,2,…,n.

由

知,当n≥3时,

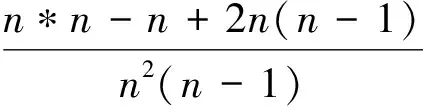
当n=2时,

同理可得u2+v2=1.因此,

uj+vj≤1,j=1,2,…,n.

□

以上求直觉判断矩阵的直觉模糊数型排序向量的方法称为直觉判断矩阵排序中转法.

由于模糊互补判断矩阵的中转法具有强条件下保序性、置换不变性等很多优良的性质,下面主要研究我们讨论的直觉判断矩阵排序中转法是否也具有类似的性质.

定理3.2直觉判断矩阵排序中转法是强条件下保序的.

假设(uij,vij)≥(ulj,vlj),j=1,2,…,n,下面证明(ui,vi)≥(ul,vl).

由定理3.1结果可知:

记∧={j|uij-vij>ulj-vlj,j=1,2,…,n}.

另外,若(uij,vij)=(ulj,vlj),j=1,2,…,n,显然有(ui,vi)=(ul,vl).

□

定理3.2的结果说明:本文给出的求解直觉判断矩阵权重向量的中转法及运用直觉模糊数的排序规则对方案进行排序是合理的.

类似于模糊互补判断矩阵是序传递的定义,我们给出直觉判断矩阵为序传递的定义.

定义3.1直觉判断矩阵Q=((uij,vij))n×n称为序传递的,若(uij,vij)≥(0.5,0.5),则任意k=1,2,…,n,有(uik,vik)≥(ujk,vjk);若(uij,vij)=(0.5,0.5),则任意k=1,2,…,n,有(uik,vik)≥(ujk,vjk),或者任意k=1,2,…,n,有(uik,vik)≤(ujk,vjk).

由定义3.1和定理3.2直接得到下述结论.

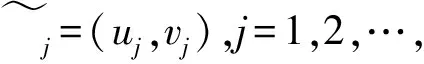
(ui,vi)≥(uj,vj)；

当(uij,vij)=(0.5,0.5)时,必有(ui,vi)≥(uj,vj),或者(ui,vi)≤(uj,vj).

最后根据定理3.1得到的uj和vj,j=1,2,…,n的表达式很容易得到以下结论.

定理3.4直觉判断矩阵排序中转法具有置换不变性.

4 实例分析

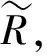
利用定理3.1的结果计算直觉判断矩阵R的权重为

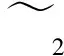
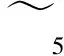
故

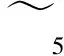
5 结论

本文主要研究了两个方面的问题.一方面是关于直觉判断矩阵的加型一致性定义的问题.虽然已经有一些学者从不同的角度对直觉判断矩阵加型一致性给出了定义(如权重范围的角度[2,26]),但是没有从直觉模糊数本身具有的特点给出直觉判断矩阵的加型一致性定义,因此我们从直觉模糊数的得分函数和精确度函数角度给出了直觉判断矩阵的加型一致性的新定义. 另一方面是关于确定直觉判断矩阵的权重问题.本文根据推导出的加型一致性等价条件运用转换函数将实际决策者给出的直觉判断矩阵转换为两个加型一致性模糊互补判断矩阵,然后对这两个矩阵运用行和归一的方法分别求出原直觉判断矩阵权重的隶属度和非隶属度,并利用直觉模糊数的排序方法进行排序.因此它是一种中转的方法,其特点是:得到的直觉判断矩阵权重结果明确、易于求解,而且具有很多优良的性质.直觉判断矩阵的权重确定方法可以应用到基于偏好信息的决策理论和方法中(如不确定性多目标决策的交互满意法),具有一定的应用价值.当然我们只是对直觉判断矩阵的权重研究作了初步探索,与其相关的问题还值得进一步研究.例如，现代技术(特别是物联网技术)迅速发展为人们提供了动态实时的决策数据，基于动态直觉模糊判断矩阵的决策和评估方法值得进一步思考.

References)

[1] Zadeh L A. Fuzzy sets[J].Information and Control,1965,8:338-353.

[2] Xu Z S. Intuitionistic Fuzzy Information Integration Theory and Application[M].Beijing:Science Press,2008.

徐泽水.直觉模糊信息集成理论及应用[M].北京:科学出版社,2008.

[3] Atanassov K. Intuitionistic fuzzy sets[M]// Sgurev V. Ⅶ ITKR’s Session. Bulg Academy of Sciences: Central Sci and Techn Library, 1984

[4] Atanassov K. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems,1986, 20:87-96.

[5] Satty T L. The Analytic Hierarchy Process[M]. New York: McGraw-Hill, 1980.

[6] Tanino T. Fuzzy preference orderings in group decision making[J]. Fuzzy Sets and Systems, 1984,12: 117-131.

[7] Xu Z S. Algorithm for priority of fuzzy complementary judgment matrix[J].Journal of Systems Engineering, 2001,16(4):311-314.

徐泽水.模糊互补判断矩阵排序的一种算法[J].系统工程学报,2001,16(4):311-314.

[8] Xu Z S. The least variance priority method (LVM) for fuzzy complementary judgment matrix[J]. Systems Engineering: Theory & Practice, 2001,21(10):93-96.

徐泽水.模糊互补判断矩阵排序的最小方差法[J].系统工程理论与实践,2001,21(10):93-96.

[9] Xu Z S. Two methods for priorities of complementary judgment matrices: Weighted least-square method and eigenvector method[J]. Systems Engineering: Theory & Practice, 2002, 22(7):71-75.

徐泽水.互补判断矩阵的两种排序方法-权的最小平方法及特征向量法[J].系统工程理论与实践,2002,22(7):71-75.

[10] Xu Z S, Da Q L.A least deviation method to obtain a priority vector of a fuzzy preference relation[J].European Journal of Operation Research, 2005, 164:206-216.

[11] Xu Z S. A survey of preference relations[J].International Journal of General Systems, 2007,36:179-203.

[12] Bustince H, Burillo P. Vague sets are intuitionistic fuzzy sets[J].Fuzzy Sets and Systems, 1996,79:403-405.

[13] Xu Z S. A practical method for priority of interval number complementary judgment matrix[J].Operations Research and Management Science,2001, 10(1):16-19.

徐泽水.区间数互补判断矩阵排序的一种实用方法[J].运筹与管理,2001, 10(1):16-19.

[14] Xu Z S. Priority method based on possibility and error analysis for interval number complementary judgment matrix[J].Journal of PLA University of Science and Technology, 2003,4(2):96-98.

徐泽水.基于可能度和误差分析的区间互补矩阵排序法[J].解放军理工大学学报(自然科学版),2003,4(2):96-98.

[15] Gong Z W, Liu S F. Research on consistency and priority of interval number complementary judgment matrix[J].Chinese Journal of Management Science, 2006,14(4):64-69.

巩在武,刘思峰.区间数互补判断矩阵的一致性及其排序研究[J].中国管理科学,2006,14(4):64-69.

[16] Liu F, Lan J B, Shi L H. An approach for interval number priority weight based on convex-combination and possibility degree[J].Fuzzy Systems and Mathematics, 2008,22(4):112-119.

刘芳,兰继斌,史丽华.基于凸组合和可能度的区间数优先权重法[J].模糊系统与数学,2008,22(4):112-119.

[17] Xu Y J, Zhang Y Z, Wei C P .Acceptable consistency analysis of interval complement comparison matrices[J].Control and Decision, 2011,26(3):327-331.

徐迎军,张玉忠,魏翠萍.区间互补判断矩阵可接受一致性[J].控制与决策,2011,26(3):327-331.

[18] Yue Q,Fan Z P,Shi L H. New approach to determine the priorities from interval fuzzy preference relations[J].Journal of Systems Engineering and Electronics, 2011, 22(2):267-273.

[19] Liu F, Zhang W G, Fu J H. A new method of obtaining the priority weights from an interval fuzzy preference relation[J].Information Sciences,2012,185:32-42.

[20] Xu Z S, Chen J. Some models for deriving the priority weights from interval fuzzy preference relations[J].European Journal of Operational Research,2008,184:266-280.

[21] Wang J, Lan J B, Ren P Y, et al. Some programming models to derive priority weights from additive interval fuzzy preference relation[J]. Knowledge-Based Systems, 2012, 27:69-77.

[22] Lan J B, Hu M M, Ye X M, et al. Deriving interval weights from an interval multiplicative consistent fuzzy preference relation[J]. Knowledge-Based Systems, 2012, 26:128-134.

[23] Wang Z J, Li K. Goal programming approaches to deriving interval weights based on interval fuzzy preference relations[J].Information Sciences,2012,193:180-198.

[24] Xu Z S. Consistency of interval fuzzy preference relations in group decision making[J]. Applied Soft Computing, 2011, 11:3 898-3 909.

[25] Li D F. Multi-attribute decision making models and methods using intuitionistic fuzzy sets[J].Journal of Computer and System Sciences, 2005,70:73-85.

[26] Xu Z S. Approaches to multiple attribute decision making with intuitionistic fuzzy preference information[J]. Systems Engineering: Theory & Practice, 2007(11):62-71.

徐泽水.直觉模糊偏好信息下的多属性决策途径[J].系统工程理论与实践,2007(11):62-71.

[27] Chen T Y. A comparative analysis of score functions for multiple criteria decision making in intuitionistic fuzzy settings[J].Information Sciences,2011,181: 3 652-3 676.

[28] Gong Z W, Li L S, Zhou F X, et al. Goal programming approaches to obtain the priority vectors from the intuitionistic fuzzy preference relations[J].Computers & Industrial Engineering, 2009,57:1 187-1 193.

[29] Gong Z W, Li L S, Forrest J, et al. The optimal priority models of the intuitionistic fuzzy preference relations and their application in selecting industries with higher meteorological sensitivity[J].Expert Systems with Applications, 2011,38:4 394-4 402.

[30] Xu Z S. Maximum deviation method based on deviation degree and possibility degree for uncertain multi-attribute decision making[J]. Control and Decision, 2001,16: 818-821.

徐泽水.基于相离度和可能度的偏差最大化多属性决策方法[J].控制与决策,2001,16:818-821.

[31] Xu Z S. A deviation-based approach to intuition fuzzy multiple attribute group decision making[J].Group Decis Negot, 2010,19:57-76.

[32] Li R J. Fuzzy Multiple Criteria Decision Making Theory and Application[M]. Beijing: Science Press, 2000.

李荣钧. 模糊多准则决策理论与应用[M].北京:科学出版社,2000.

[33] Xu Z S. Intuitionistic preference relations and their application in group decision making[J].Information Sciences,2007,177:2 363-2 379.

Deriving intuitionistic fuzzy number priority weights from intuitionistic judgment matrix

TU Zhenkun1,2, LIU Xinbao1

(1.School of Management, Hefei University of Technology, Hefei 230009, China;2.School of Mathematics, Hefei University of Technology, Hefei 230009, China)

The problem of the weights of intuitionistic judgment matrix (IGM) was discussed, and the consistency of IGM, which is related to the reliability of the weights, was explored. From the perspectives of the score function and accuracy function of intuitionistic fuzzy value, a new definition of additive consistency of IGM was given, and an equivalent condition for additive consistency was achieved. To make full use of the information of the original IGM and make the decision meet the consistency, the original IGM was converted into two additive consistency fuzzy judgment matrices, which was achieved by the transformation function arising from the equivalent condition. The membership degree and the non-membership degree of the original IGM’s weights were respectively achieved by normalizing rank aggregation to the two additive consistency fuzzy judgment matrices. Thus the intuitionistic fuzzy number priority weights of the IGM were obtained, and ranked with a sequencing rule for intuitionistic fuzzy values. The excellent properties of the proposed method were discussed, and its validity and practicability were illustrated in an example.

intuitionistic judgment matrix; intuitionistic fuzzy number priority weight; middle translation method; consistency

0253-2778(2013)05-0420-09

C934

A

10.3969/j.issn.0253-2778.2013.05.010

Tu Zhenkun, Liu Xinbao. Deriving the intuitionistic fuzzy number priority weights from intuitionistic judgment matrix[J]. Journal of University of Science and Technology of China, 2013,43(5):420-428.

涂振坤，刘心报. 直觉判断矩阵的直觉模糊数型权重研究[J]. 中国科学技术大学学报，2013,43(5):420-428.

2012-11-26；

2013-03-03

国家自然科学基金(71231004，71171071)资助.

涂振坤(通讯作者),男,1978年生,博士生/讲师. 研究方向:模糊决策. E-mail:zhenkuntu@126.com