基于长径比修正的飞艇对流换热准则关系式研究

刘 泉，徐庶民，钟 伟，杨渐志，刘明侯

(1.中国科学技术大学热科学和能源工程系，安徽合肥 230027；2.中国科学技术大学工程与材料科学实验中心，安徽合肥 230027)

基于长径比修正的飞艇对流换热准则关系式研究

刘 泉1，徐庶民2，钟 伟1，杨渐志1，刘明侯1

(1.中国科学技术大学热科学和能源工程系，安徽合肥 230027；2.中国科学技术大学工程与材料科学实验中心，安徽合肥 230027)

飞艇热控制是平流层飞艇应用中涉及的关键技术之一，而外部对流换热是平流层飞艇热控制的重要影响因素.为了准确预测飞艇换热，基于数值模拟，建立基于飞艇长径比的对流换热准则关系式，并与实验结果比较，发现其预测误差为±7%.与0°攻角换热相比，15°攻角时迎风面换热比背风面增大了10%左右，而总体换热增大7%.

平流层飞艇；热控制；热模型；对流换热；数值模拟；实验研究

0 引言

平流层飞艇定点或机动巡航在临近空间底部，具有驻空时间长、载重量大、可重复使用等特点[1]，在区域防灾、环境监测、城市安全监控、高分辨率实时区域监测、通信等方面具有重要的用途.飞艇虽配有螺旋桨推进装置以获得前进动力，但主要依靠静浮力获得升力[2].其浮力决定于囊体内气体温度与环境空气温度差.临近空间飞行器与外部环境换热主要包括对流和辐射两种形式.辐射包括太阳直射、大气散射、地面反照、地面和大气红外辐射.对流部分包括浮空器蒙皮与外部大气的强迫对流与自然对流、内部气体的自然对流等.飞艇飞行时，白天太阳辐射近似太阳常数，因而飞艇囊体温度高于环境(超热)；夜间时，飞艇向周围散热，其囊体温度将会降低，甚至低于环境温度(超冷).相关研究表明，飞艇昼夜温差可达70～90 K[2-8]，有时甚至超过100 K.显著的昼夜温差会导致飞艇静浮力有较大变化，进而导致飞艇定点困难.另外，飞艇囊体超热会导致超压问题，影响飞艇安全.因此，平流层飞艇热控问题吸引了研究者关注.

方贤德[2]等用两节点稳态模型计算了高空飞艇平衡温度.外部对流换热采用球体准则，内部自然对流选取水平热平板的顶表面或冷平板的底表面实验关系准则.Rapert[6]将基本的传热学经验公式用于双气囊平流层飞艇建立其热控模型.对于自然对流，假设飞艇为一水平长圆柱体，选取圆柱换热实验关系式作为其对流换热系数计算准则；对于强迫对流，则假设飞艇为一简单平板，等效长度与飞艇相同，等效面积为飞艇表面积.Cao等[7]分别建立了平流层飞艇辐射换热模型和对流换热模型，对飞艇进行了热阻网络分析，并用集总热容的方法计算了飞艇温度场沿海拔高度的分布情况.李德富等[8]建立了超高空低速飞行器的热环境分析模型，对超高空低速飞行器进行数值模拟，研究热辐射和对流换热对超高空低速飞行器热环境特性的影响.文中采用平板的实验关联式确定飞行器表面的局部对流换热系数.

纵观已有的热分析模型发现，相关平流层飞艇热模型中，研究者根据不同飞艇形状差异采用不同的经验准则，如平板、圆球或圆柱的经验对流换热准则进行计算.由于准则不同，模拟结果存在不小差异.因此有必要对椭球体的飞艇建立自身的对流换热模型.本文采用数值与实验相结合手段，建立基于外形修正(长径比)的飞艇对流换热特性准则关系式，并研究攻角对其换热特性的影响.

1 数值模拟

1.1 建模

本文采用飞艇形状类似于旋转椭球体，其长径比为2的几何型面来自某飞艇实际参数，模型如图1所示.建立几何模型时，用一个圆柱体大气空间包裹飞艇.对于0°攻角计算，可简化为二维轴对称问题.对于有一定攻角问题，则是三维问题.

图1 飞艇模型示意图

数值模拟时采用的控制方程及边界条件如下：

连续方程

(1)

动量方程

(2)

式中，

能量方程

(3)

湍动能输运方程

(4)

耗散率输运方程

(5)

求解时，给定速度进口，出口为压力出口.

有攻角三维求解采用非结构网格；二维轴对称全场采用结构网格.在靠近壁面处加密处理.速度和能量都采用一阶迎风格式离散，压力速度耦合采用Simple算法.

为了与实验结果比较，计算中对模型内采用内热源方法加热.实验中，基于来流速度U∞和飞艇特征尺度d的雷诺数Re=U∞d/ν>1.5×105，为超临界湍流.数值模拟时，为了使得准则关系雷诺数覆盖实验参数，最小雷诺数为8.5×104，为亚临界湍流.由于强迫对流占主导地位，计算中忽略自然对流.空气密度等物性参数是温度的函数[7].

经典传热学理论[9]认为，对流换热系数影响因素包括流动起源(强迫对流、自然对流)、流动有无相变、流动状态(层流、湍流)、换热表面的几何因素(几何形状、表面粗糙度)、流体的物理性质等，与壁面温度无关.故可在飞艇模型中设置一个恒定的内热源，以此求得飞艇表面的平均对流换热系数，飞艇材料取为铝质，这样即可得到一个较为均匀的表面温度.

一般对流换热关系式有两种形式：①流体物性采用膜温Tf计算；②流体物性采用T∞计算，并乘上(Pr∞/Prs)r类似形式的参数，r一般可取1/4.由于本文主要研究的是雷诺数中速度变化导致的对流换热影响，而高流速使得对流换热温差偏小，壁温与来流的温差基本在50 K以内，空气Pr数变化约为1%，故采用T∞计算流体物性，并将(Pr∞/Prs)r参数忽略.

为了研究长径比影响，取模型长轴为l≈0.3 m不变，通过变化短轴引起长径比l/d变化，共数值模拟计算6，3.75，3，2.5，2等5个工况.飞艇模型中内热源功率恒定为500 W.假定飞艇静止，空气来流速度在5～40 m/s之间变化，来流温度为300 K.环境压力和温度分别为101.325 kPa和300 K.

1.2 数值模拟目标

考虑到该模型近似为旋转椭球体，当其长、短轴之比为1时，即近似为球体，此时换热准则当与球准则类似；而当长、短轴之比很大时，又近似为圆柱，展开可视作平板，应与平板准则类似.因此，该模型的对流换热准则形式上应当与平板、球等普遍准则相同，并考虑将长、短轴之比作为影响因子加入准则中.此处定义飞艇的形状因子长径比，即l/d，飞艇长短轴如图1所示.

最终，我们需建立的对流换热关系式为

(6)

形式.式中c1，c2，c3为需要确定的常数.Nu数是Re数、长径比l/d的函数.由于计算过程中空气温差并不大，此处假设Pr为常数0.7，且对Nu的影响取Pr1/3，即符合圆柱或平板速度边界层与温度边界层厚度之比[9].

1.3 数值模拟结果

对于给定来流和某长径比模型，就会得到一个飞艇模型的平均Nu数.将40组Nu-Re-l/d的数据采用最小二乘法进行拟合，得如图2所示曲线，并与圆球、平板等普遍换热准则进行比较.

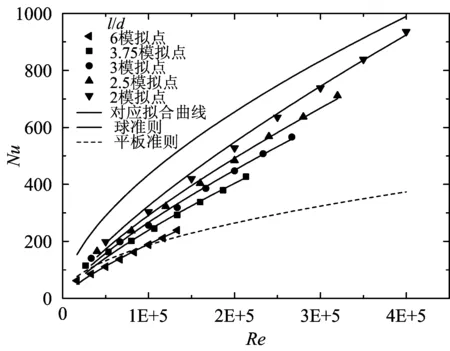
图2 对流换热准则拟合曲线

从图2中可以看到，长径比l/d对Nu-Re关系有明显影响，长径比越小，Nu数越大.而当长径比一定时，Nu数随Re数增大而增大.

随着长径比的增大，模型形状越显长且细，其换热应当接近平板.如图2所示，当l/d=6时，其换热Nu-Re-l/d曲线与平板的Nu-Re曲线较为接近.但由于两者本身形状的根本差异，反映在Nu-Re换热曲线上，其曲率不同.反之，随着长径比的减小(l/d>1)，模型形状则越接近球体.相比于其他更大的长径比，l/d=2模型的Nu-Re-l/d曲线最接近球换热准则曲线.

可见，不同的长径比导致的模型换热差异较大.而特定的模型如用平板、圆球等普遍换热关系式进行计算，也将导致结果存在较大偏差.如模型l/d=2时，运用圆球准则计算换热将导致最高30%的偏差，而平板准则在较大雷诺数时偏差更甚.基于l/d，最终建立如下对流换热准则：

(7)

1.4 数值模拟攻角对换热影响

飞艇悬浮在平流层时，其长轴并不总是与来流平行.换言之，飞艇与来流方向可能会存在一定攻角.这时飞艇附近流场有一定变化，其必然导致换热变化.本文数值模拟时，其工况与节1.2相同，仅仅旋转模型，使得模型与来流方向存在一定攻角.此时，计算模型由二维轴对称换热变为三维换热.考虑长径比l/d=2的模型，分别计算了攻角0°和15°时的对流换热状况.计算结果如图3所示，详细参数见表1.

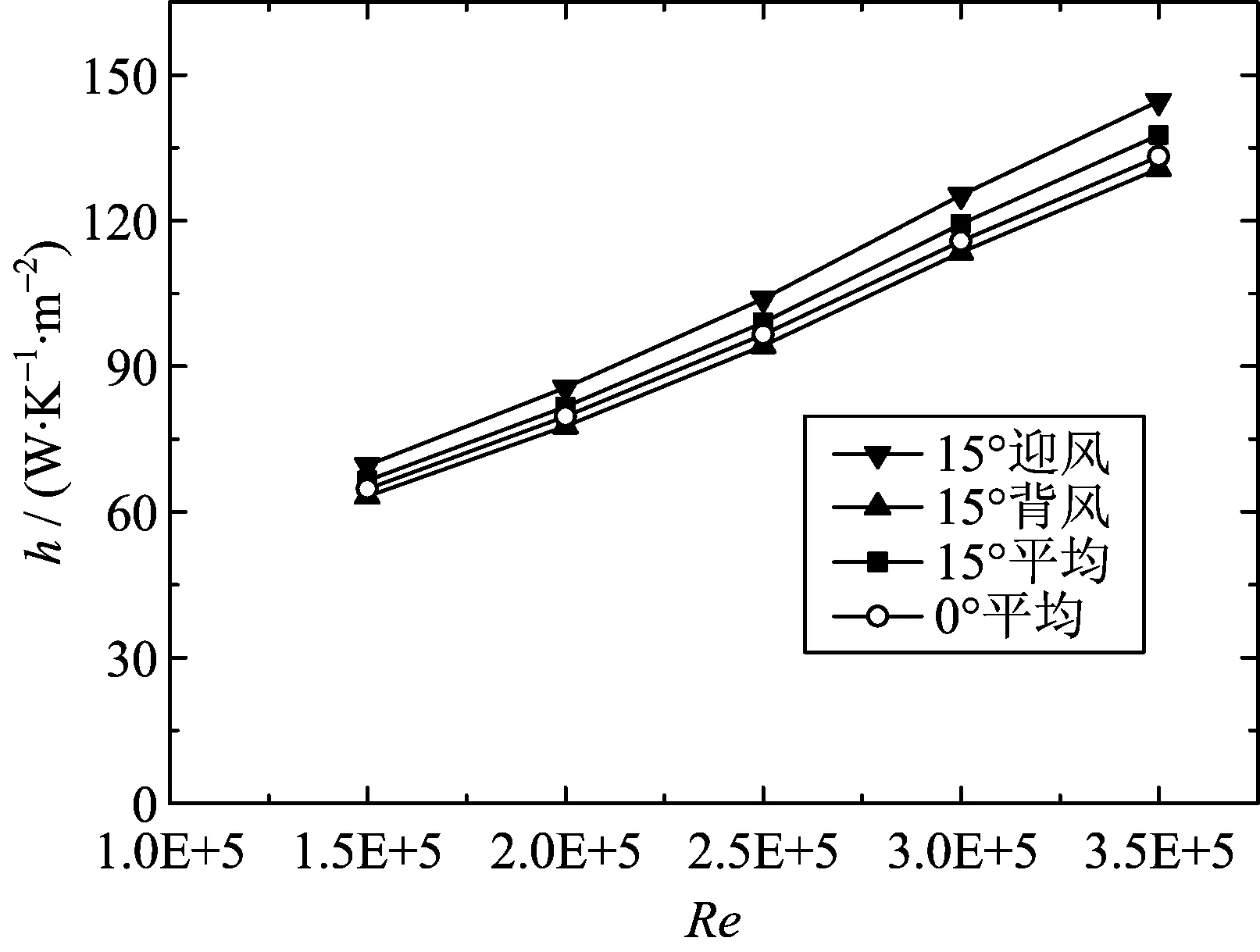
图3 攻角对换热系数的影响

当飞艇攻角为15°时，迎风面会导致局部流体加速，故换热较好，背风面则换热较差，二者相差约10%.虽然迎风面与背风面换热有较大差异，但对于整个飞艇，攻角的存在对平均换热影响仅增大3%左右，模型换热略微变好.虽然攻角对平均换热影响较小，但当飞艇有一定攻角飞行时，太阳方位角与迎风面或背风面协同情况对系统热平衡会产生较大影响.在实际热设计时，应考虑该问题.

2 实验验证

2.1 实验设置

为了验证上述用数值模拟建立的经验准则的正确性，加工了3个铝质模型，长径比分别为2，3，6，开展对流换热实验.实验系统装置连接及模型表面热电偶布置如图4所示.在模型表面等距打孔3×9个，孔深2 mm，直径1 mm，总共可容纳27个T型热电偶，用于测量表面温度.并在来流的上游布置1个T型热电偶，用于测量来流温度.实验在1 m×1 m的低速风洞中进行.实验风速分别为15.5，26.7，39.8 m/s.加热棒功率通过万能表测量计算确定，为Q=221.5 W，由于铝表面的发射率较低，且实验中模型与外界温差不大，故忽略模型辐射热损失.热电偶数据通过Agilent数据采集仪录入PC，保存有效实验数据均在T-t(s)曲线缓慢变化30 min后，此时温度值1 min内变化小于0.1 K.

实验完成后，对每个工况27个温度数据求平均值，近似认为所得结果为该工况下飞艇表面平均温度，借助来流温度，即可得到温差ΔT，再利用式(8)，即可求得换热系数h.进而利用空气参数表查得对应温度下空气导热系数λ与黏性系数ν，通过式(9)得到Nu数.

(8)

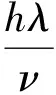
(9)

2.2 误差分析

实验中，功率Q=I2R，通过检测加热棒电流和电阻计算得到.万用表检测电流和电阻分别精确到0.1 A和0.1 Ω，其相对误差分别为1%和1%，则功率的相对误差为3%.热电偶测温精度为0.2 K，温差最大误差0.4 K.测温过程中最小温差为11.8 K,则其相对误差为3.3%.忽略对流换热面积误差，则对流换热系数最大误差为6.3%.如果长度误差1%，忽略导热系数误差，则Nu最大误差为7.3%.

表1 0°攻角与15°攻角模拟数据对比

图4 实验系统示意图

2.3 实验结果

3个长径比模型对流换热数据与数值模拟曲线对比如图5所示.图中，实线为基于长径比修正准则公式(7)的计算值，离散符号表征实验值.从图中发现，对于不同长径比和3个雷诺数工况条件下，两者最大误差为±7%.由此可见，本文建立的基于长径比修正的经验准则对飞艇强迫对流换热具有较高的预测精度.另外，实验结果充分证明了飞艇随长径比变化，换热特性有明显变化.

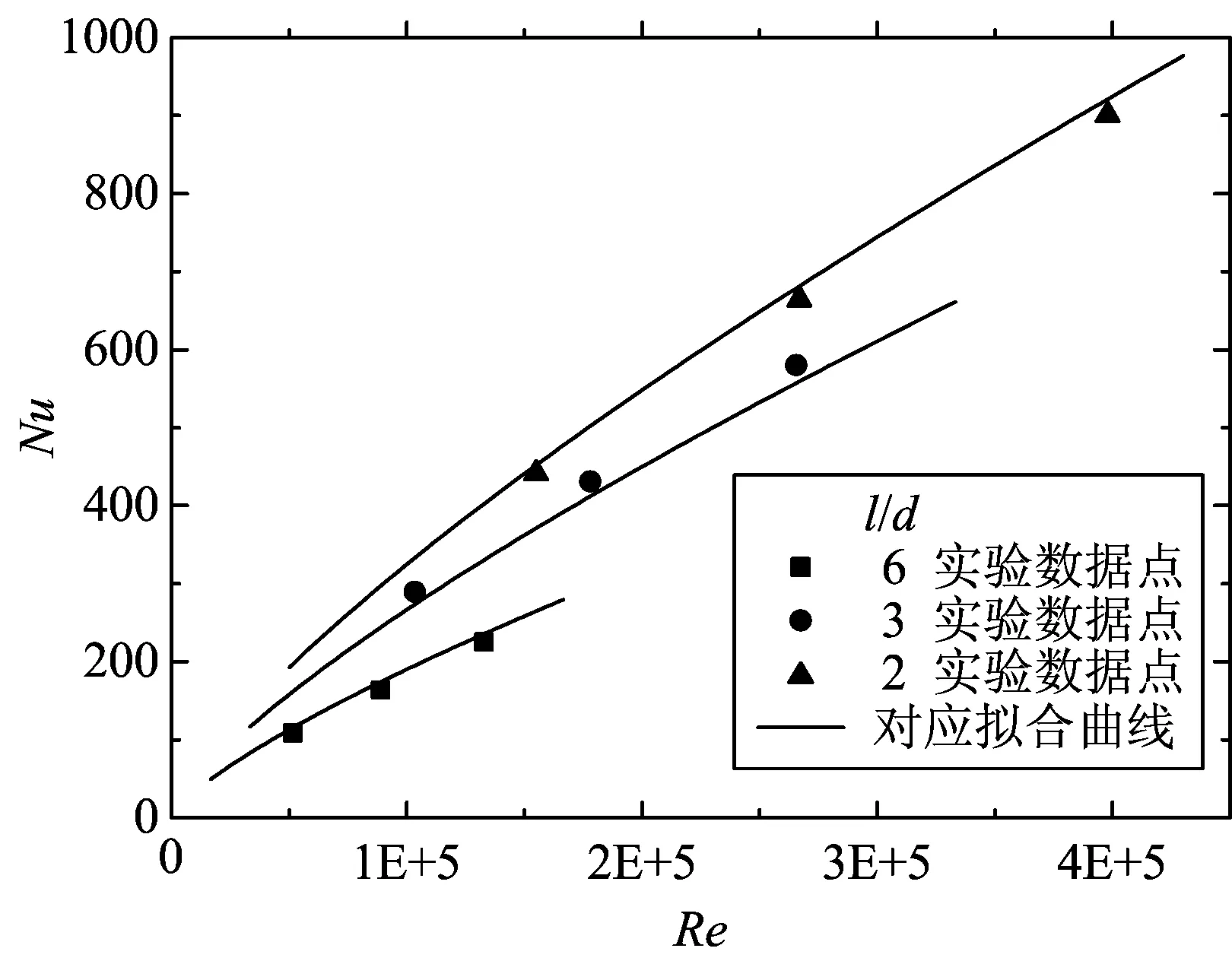
图5 l/d分别为6，3，2的实验数据和经验准则曲线

2.4 实验研究攻角对换热系数影响

实验中测了长径比2∶1模型在0°和15°攻角时强迫对流换热特性.实验结果如表2和图6所示.

实验结果表明，攻角使迎风面局部气流加速，导致其换热提高，而背风面换热则变差.迎风面与背风面换热差异约10%～20%.在研究的雷诺数变化范围内，随着雷诺数增大，迎风面与背风面换热差异有增大趋势.这与数值模拟结果相互印证.然而，在数值模拟中，攻角为15°时，平均对流换热系数仅比0°攻角提高3%；而实验发现，攻角提高后，平均对流换热系数提高约7%左右.其主要原因是数值模拟中采用的标准k～ε可能对背风面流场结构计算有较大误差，导致换热模拟结果偏低.从实验结果可以推测，如果要建立高精度的平流层飞艇对流换热经验准则，除了长径比，攻角也应该是一个重要参数，这在以后的研究中应予以关注.

图6 长径比2∶1时存在15°攻角换热系数

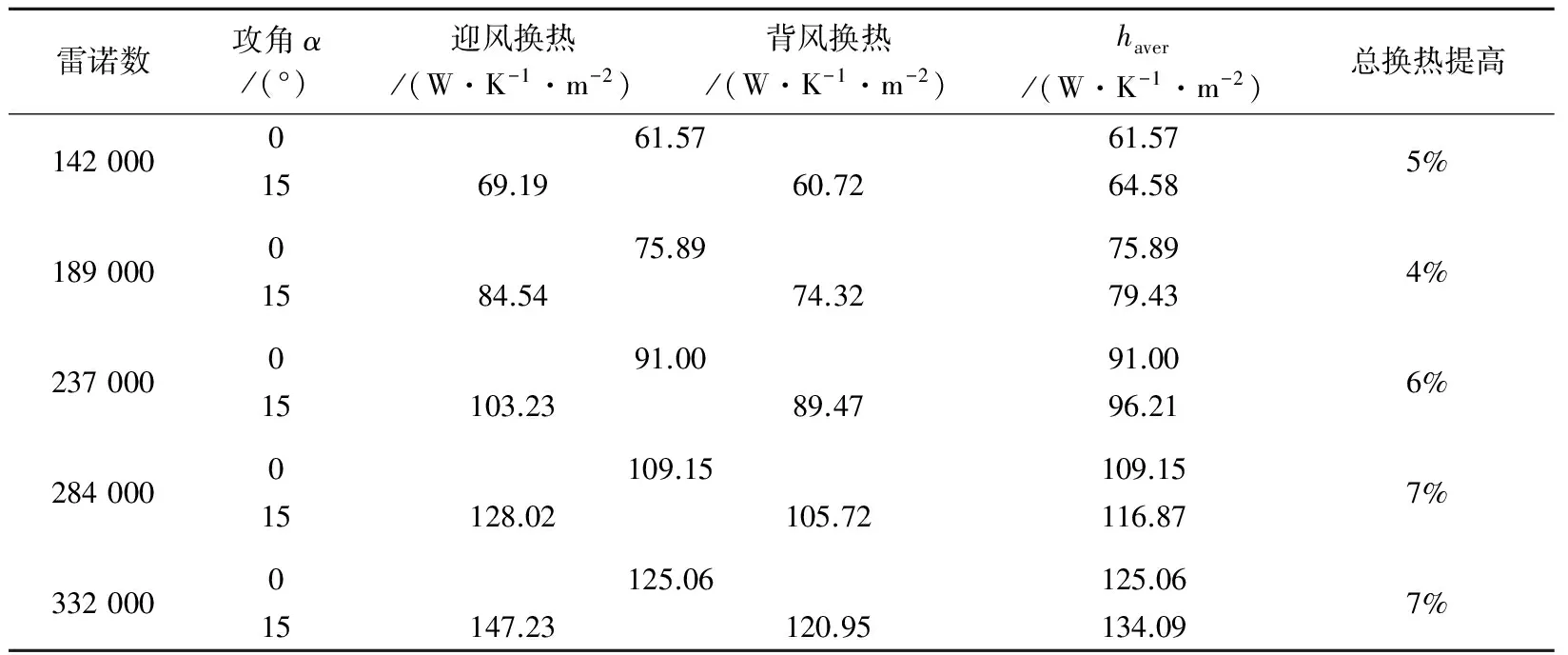
表2 有、无攻角实验数据对比

3 结论

为考虑外形对换热的影响，本文采用数值方法建立了基于飞艇长径比修正的对流换热模型，经过3个长径比、3个雷诺数实验验证，本文建立的经验准则结果与实验值误差小于7%.

数值与实验结果表明，飞艇15°攻角运行时，其迎风面换热较背风面有10%加强.飞艇实际运行时，太阳方位角与飞艇攻角对整个飞艇热平衡会有较大影响.数值模拟中，攻角从0°增大到15°，其总体换热增大仅3%，但实验结果却增大7%，表明本文采用的数值模拟对背风面换热预测精度有待提高.

本文研究结果表明，飞艇对流换热模型需要考虑长径比和攻角的影响.由于实验模型与实际飞艇尺度相差较大，雷诺数对换热准则的影响有待进一步验证.

References)

[1] 王彦广，姚伟，李勇.平流层飞艇技术发展及其应用前景展望[J].卫星与网络,2010(4):18-21.

[2] Fang Xiande，Wang Weizhi， Li Xiaojian. A study of thermal simulation of stratospheric airships[J]. Spacecraft Recovery & Remote Sensing，2007，28(2): 5-9.

方贤德，王伟志，李小建. 平流层飞艇热仿真初步探讨[J]. 航天返回与遥感，2007，28(2):5-9.

[3] Liu Dongxu，Yang Yongqiang，Lu Mingyun，et al. Effect of envelop thermal radiative properties on the stratospheric super-pressure LTA vehicle helium temperature[J]. Journal of Beijing University of Aeronautics and Astronautics， 2010， 36(7):836-840.

刘东旭，杨永强，吕明云，等.蒙皮热辐射特性对平流层浮空器氦气温度影响[J].北京航空航天大学学报，2010, 36(7):836-840.

[4] Xu Xianghua，Cheng Xuetao，Liang Xingang. Thermal analysis of a stratospheric airship[J]. Journal of Tsinghua University (Science and Technology)，2009，49(11): 1 848-1 851.

徐向华，程雪涛，梁新刚. 平流层浮空器的热数值分析[J].清华大学学报(自然科学版)，2009，49(11)：1 848-1 851.

[5] Wang Y W，Yang C X.A comprehensive numerical model examining the thermal performance of airships[J]. Advances in Space Research, 2011，48：1 515-1 522.

[6] Rapert R M. A heat transfer model for a hot helium airship[R]. NASA STI/Recon Technical Report A, 1987, 87: 48 646.

[7] Cao K，Baker J. Multimode heat transfer in a near-space environment[J]. Heat Transfer Engineering, 2010, 31(1)：70-82.

[8] Li Defu，Xia Xinlin，Dai Guilong. Thermal environment characteristics of low-speed aircrafts at extremely high altitude[J]. Journal of Harbin Institute of Technology，2009,41(7):60-63.

李德富，夏新林，戴贵龙. 超高空低速飞行器的热环境特性[J].哈尔滨工业大学学报，2009,41(7):60-63.

[9] Incropera F P， DeWitt D P， Bergman T L，et al. Fundamentals of Heat and Mass Transfer[M]. 6th ed. New York: John Wiley & Sons， 2006.

A heat transfer empirical correlation for the stratospheric airship based on its length-to-diameter ratio

LIU Quan1, XU Shumin2, ZHONG Wei1, YANG Jianzhi1, LIU Minghou1

(1.Department of Thermal Science and Energy Engineering, University of Science and Technology of China, Hefei 230027, China;2.Public Experimental Center of USTC, University of Science and Technology of China, Hefei 230027, China)

Thermal control is one of the key technologies involved in stratospheric airship applications, and convective heat transfer is an important factor in the thermal control of a stratospheric airship. In order to accurately predict the heat transfer of an airship，using the numerical method, an empirical correlation ofNunumber as a function ofRe,Prandl/d(length to diameter ratio) was established. Compared with experimental data, the uncertainty of the empirical correlation is about ±7%. The effect of the attack angle of an airship on heat transfer performance was evaluated. It was found that the heat transfer at the windward side is 10% higher than that of the leeward side, while the average heat transfer of airship is 7% higher when the attack angle changes from 0° to 15°.

stratospheric airship； thermal control； thermal model； convective heat transfer； numerical simulation； experimental study

0253-2778(2013)05-0387-06

TK172

A

10.3969/j.issn.0253-2778.2013.05.006

Liu Quan, Xu Shumin, Zhong Wei, et al. A heat transfer empirical correlation for the stratospheric airship based on its length-to-diameter ratio[J]. Journal of University of Science and Technology of China, 2013,43(5):387-392.

刘泉，徐庶民，钟伟，等. 基于长径比修正的飞艇对流换热准则关系式研究[J]. 中国科学技术大学学报，2013,43(5):387-392.

2012-12-03；

2013-03-26

国家自然科学基金(11172296)资助.

刘泉，男，1990年生，硕士生. 研究方向：平流层飞艇热控制. E-mail:lquan64@mail.ustc.edu.cn

刘明侯，博士/教授. E-mail: mhliu@ustc.edu.cn