基于折线包络的经验模态分解方法*1

杨彩红 梁建文 张郁山

1）中国地震灾害防御中心，北京 100029

2）天津大学土木工程系，天津 300072

引言

1998年，Huang等（1998）提出了处理非平稳信号的HHT方法（Hilbert-Huang Transform，简称HHT）。该方法包括2个步骤：①任意信号首先经过经验模态分解方法（Empirical Mode Decomposition，简称 EMD）被分解为一系列固有模态函数（Intrinsic Mode Function，简称IMF）；②对每个IMF进行Hilbert谱分析（Hilbert Spectral Analysis，简称HSA），得到相应的Hilbert谱，最后将所有IMF的Hilbert谱相加得到原始信号的Hilbert谱。Hilbert谱将原始时域信号表示在联合的时间-频率域上，是原始信号的一种时频表示。HHT方法自提出后，已经在地震动的地震学与工程学特性研究（Huang等，2001；Zhang等，2003；Loh等，2001）与结构系统识别领域中得到了应用（Yang等，2003a；2003b；2003c；Salvino，2000；Pines等，2001；Zhang等，2005；石春香等，2005），而且一些学者针对HHT方法自身存在的问题也展开了研究工作（Huang等，1999；邓拥军等，2001；张郁山等，2003；黄大吉等，2003；罗奇峰等，2003）。

针对传统的EMD方法分解长周期信号所面临的问题，本文提出了基于折线包络的经验模态分解方法，通过与已有EMD方法的比较论证了该方法的分解效率，并利用数值算例验证了该方法所得结果的意义。

1 基本方法

1.1 基于样条包络的“筛分”

在HHT方法中，IMF是满足如下2个条件的信号：①在信号的整个持续时间内，零交点（波形曲线与零轴的交点）的数目与极值点的数目必须相等或至多相差一个；②在任意时刻，由极大值点定义的上包络线和由极小值点定义的下包络线之间的平均值为零。利用EMD方法，任意信号可以被分解为若干IMF分量。Huang等（1998）详细描述了EMD方法分解信号的具体过程，此处不再赘述。EMD对信号分解的核心运算是其“筛分”处理（sifting process）。传统的“筛分”过程处理信号x(t)的具体运算如下：

1）将x(t)波形中所有局部极大值点和局部极小值点识别出来；

2）用三次样条曲线将所有局部极大值点连接起来构成原始波形的上包络线u()e t~ ，同样再用三次样条曲线将所有局部极小值点连接起来构成原始波形的下包络线d()e t~ ，上下包络线应将原始波形包在中间；

上述过程即称为一次“筛分”。本文的研究既是针对该筛分过程进行的改进，此处将该“筛分”处理定义为基于样条包络的“筛分”，记作

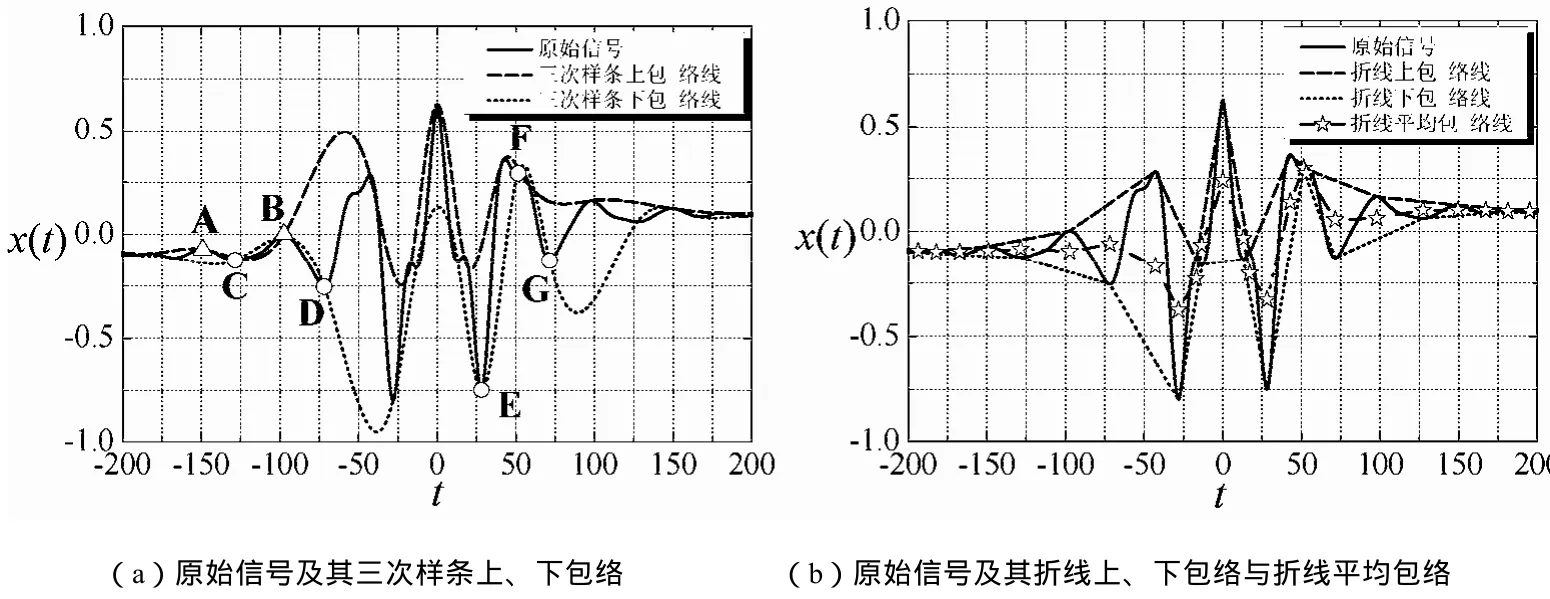
图1 原始信号及其三次样条包络与折线包络Fig. 1 Original signal and its cubic-spline envelopes and folding-line envelopes

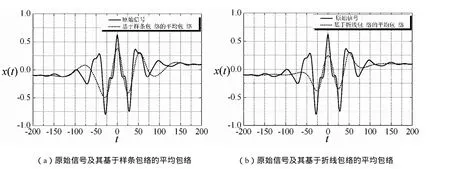
图2 原始信号及其两种平均包络Fig. 2 Original signal and its two kinds of mean envelopes

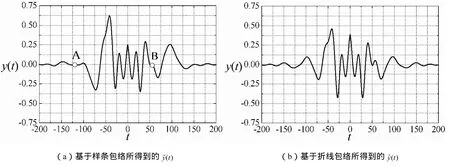
图3 两种筛分方法所得到的结果Fig. 3 Results of two sifting methods

传统的EMD方法利用上述“筛分”处理分解长周期信号时，由于信号相邻极值点之间的距离较长，连接信号极值点的三次样条包络线在信号的相邻极值点之间将会出现较大的“抖动”，这将导致信号的三次样条上、下包络线不能很好地包络原始信号，信号的平均样条包络线也不能很好地分割原始信号，从而会影响EMD方法的分解效率。考虑信号x(t)，其波形如图1（a）中实线所示，基于样条包络EMD方法在对其进行“筛分”处理时，首先将其所有极大值点和所有极小值点分别用三次样条曲线连接起来形成三次样条上、下包络线，分别如图1（a）中的虚线与点线所示。从中可以看出，由于x(t)的两个相邻极大值点A、B和两个相邻极小值点C、D相距较远，三次样条上包络线在A点与B点之间出现了比较大的“抖动”，同样，三次样条下包络线在C点与D点之间也出现了比较大的“抖动”。这就导致了在C点与B点之间，三次样条下包络线反而位于上包络线之上，如图所示。此外，尽管下包络线在三个相邻极小值点E、F与G之间“抖动”不大，但在t=50之后依然出现了下包络线位于上包络线之上的现象。这种由于三次样条曲线的“抖动”而导致的下包络线在某些区间位于上包络线之上的现象必然会使得三次样条上、下包络线不能很好地包络原始信号，从而会影响EMD方法的分解效率。基于上述考虑，本文提出一种基于折线包络的EMD方法。

1.2 基于折线包络的“筛分”

基于折线包络的EMD方法依然利用“筛分”处理来分解原始信号。针对原始的基于样条包络的EMD方法所面临的问题，基于折线包络的EMD方法对信号x(t)的“筛分”处理过程如下：

1）将原始信号x(t)的所有极大值点用直线段连接起来形成原始信号的折线上包络eˆu( t)；将原始信号的所有极小值点用直线段连接起来形成原始信号的折线下包络eˆd( t)；

3）将折线平均包络mˆ0( t)的所有折点用三次样条曲线连接起来即形成原始信号的均值包络 mˆ( t)；

4）原始信号x(t)减去上述均值包络 mˆ( t)即得到一个新的信号y(t)。

上述过程即为基于折线包络的EMD方法的一次“筛分”，此处称之为基于折线包络的“筛分”，该过程可用符号ˆS表示，即：

下面比较这两种“筛分”的处理过程。考虑到图1所示信号，在传统的基于样条包络的“筛分”处理中：首先将原始信号x(t)的所有极大值点和所有极小值点分别用三次样条曲线连接起来形成上、下包络线，如图1（a）中虚线与点线所示；这两条包络的均值即为基于样条包络的平均包络 ()m t~ ，如图2（a）中点线所示；原始信号x(t)减去此平均包络0()m t~ 即得到一个新的信号 ()y t~ ，如图3（a）所示。

基于折线包络的“筛分”处理，首先将原始信号 x(t)的所有极大值点和所有极小值点分别用直线段连接起来形成折线上、下包络，它们的均值即为原始信号的折线平均包络，如图1（b）所示；该折线平均包络的折点所在位置与原始信号极值点所在位置相同，如图所示。将该折线平均包络的所有折点用三次样条曲线连接起来即形成基于折线包络的平均包络如图2（b）所示；相比基于样条包络的平均包络，基于折线包络的平均包络 m~ ( t)更好地分割了原始信号的波形，如图2所示。将原始信号x(t)减去此平均包络 ()m t~ 即得到一个新的信号ˆ()y t，如图3（b）所示。相比图3（a）所示基于样条包络“筛分”所得到的 ()y t~ ，ˆ()y t的波形更接近本征模态函数（IMF）的要求：①相比 ()y t~ ，ˆ()y t的波形关于零轴更加对称；②ˆ()y t的所有极大值点均位于零轴以上，所有极小值点均位于零轴以下，而在 ()y t~ 的波形中依然存在着位于零轴以下的极大值点，如图3（a）所标记的A、B两点。

通过以上比较可以看出，基于折线包络的平均包络线更好地分割了原始信号，利用它进行一次“筛分”处理所得结果的性态更接近IMF的要求，因此相比基于样条包络的“筛分”方法，基于折线包络的“筛分”方法具有更高的分解效率。

1.3 基于折线包络的EMD方法

由于信号的波形中存在着隆起及其他高阶导数不连续的奇点，上述一次“筛分”并不能得到满足要求的IMF分量，通常需要多次“筛分”过程进行处理，最终所得信号才能满足IMF分量的要求。对原始信号进行k次“筛分”处理可以记为：

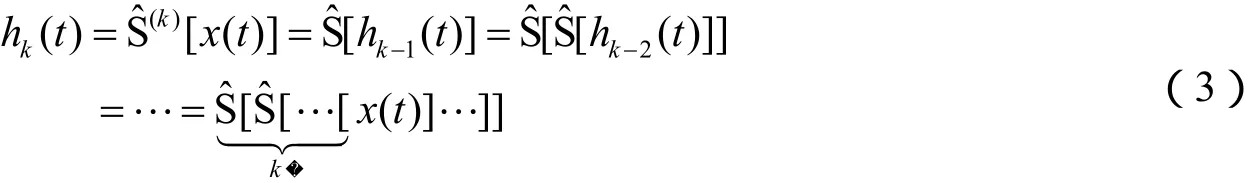
仿照传统EMD方法的处理过程，本文提出的基于折线包络EMD方法的处理流程如下：

1）记对原始信号x(t)进行k1次与k1-1筛分所得结果为若它们之间的标准差：

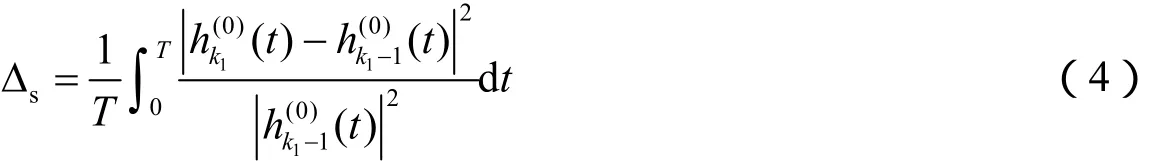
满足Δs＜0.3，则为信号x(t)的第一个IMF分量c1(t)：

2）令

若对 r1( t)筛分k2次后的结果与k2-1次的结果之间的标准差（按照公式（4）计算）满足Δs＜0.3，则为原始信号的第二个IMF分量：

3）将上述分解过程重复，即可得到原始信号的一系列IMF分量：

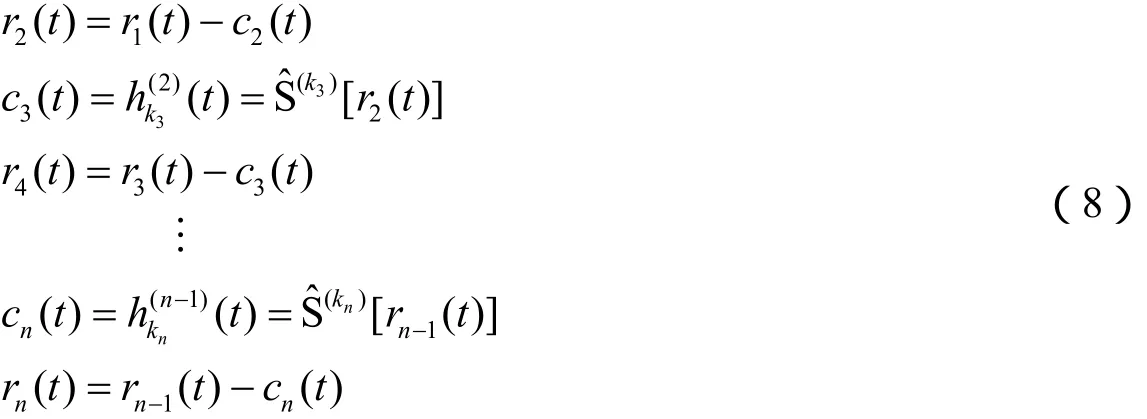
4）如果最后得到的IMF分量cn(t)或残余信号rn(t)的值非常低，低于预先设定好的值；或者最后的残余信号rn(t)为时间的单调函数，在其波形中不存在极值点，那么上述分解过程结束。

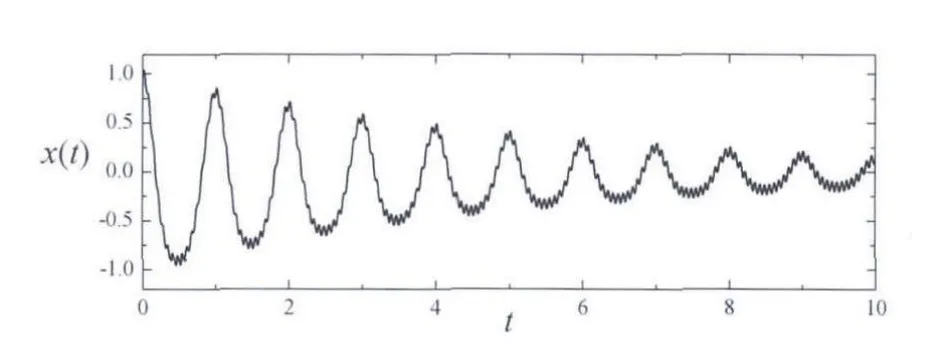
图4 含高频正弦噪声的衰减余弦调频波Fig. 4 Attenuated frequency-modulated cosine wave containing sinusoidal noise

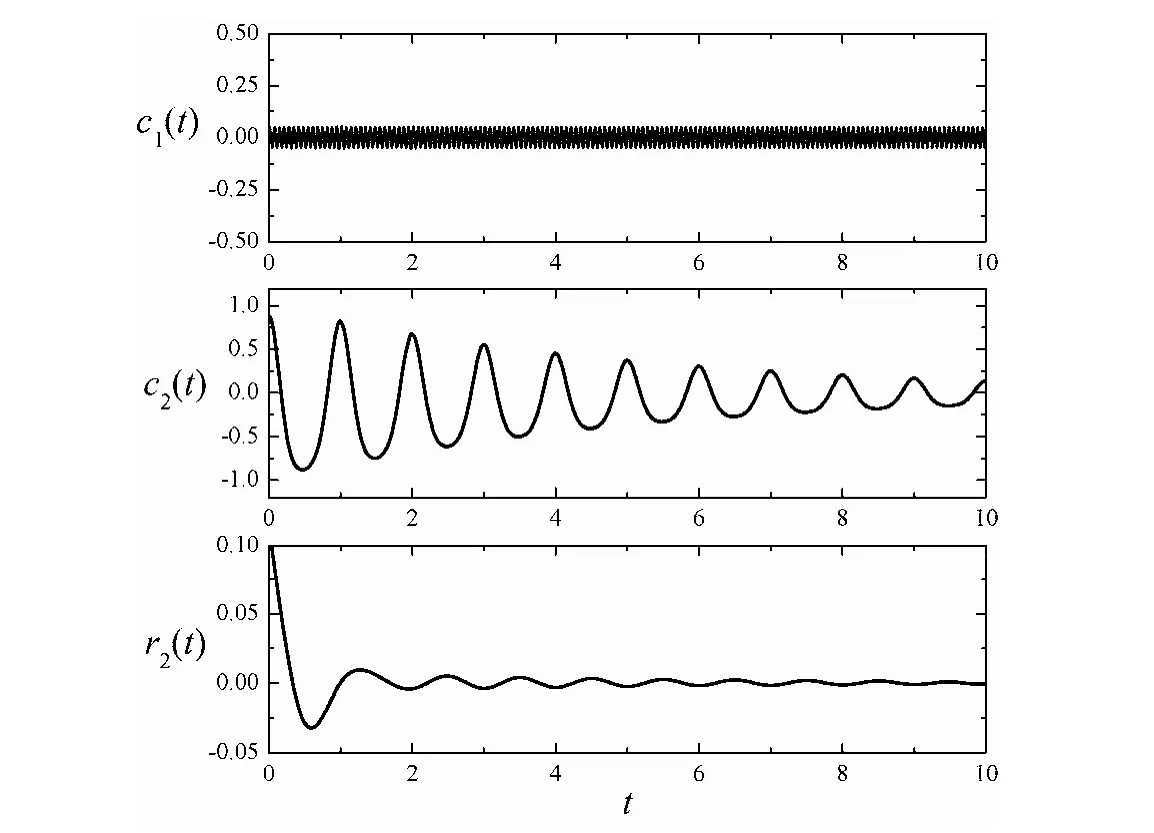
图5 基于折线包络的EMD方法分解图4所示信号所得到的主要IMF分量与残余分量Fig. 5 Main IMF components and residue obtained by decomposing the signal shown in Fig. 4 using the folding-line-envelope-based EMD method

2 算例

2.1 具有明确解析式的信号

考虑如图4所示含噪声的衰减余弦调频波x(t)=x1(t)+x2(t)，该信号由幅值衰减的余弦调频波

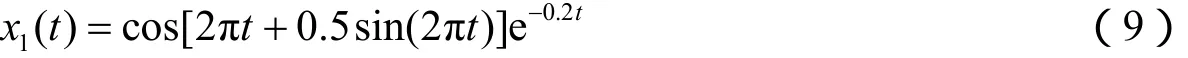
与高频正弦噪声

共同合成。其中信号x1(t)的瞬时频率fi1(t)定义为其相位的导数

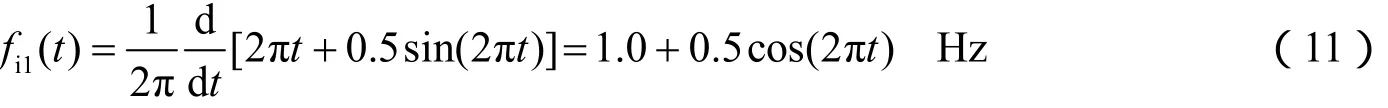
可以看出，其瞬时频率随时间作简谐波动，其幅值随时间呈指数衰减，衰减因子为0.2。应用基于折线包络的EMD方法对信号x(t)进行分解将会得到12个IMF分量，其中前两个分量c1(t)和c2(t)幅值明显高于其余分量，具有明确的数学意义；其余分量的幅值较小，它们的出现主要是由数值误差引起的，它们的和为r2(t)。c1(t)、c2(t)与r2(t)的波形如图5所示，可以看出：r2(t)的幅值在初始时刻较大，但仍未超过0.1，它主要是由于EMD方法中数据边界误差引起的；在其余大部分时段内，r2(t)的幅值在一个非常小的范围内波动。IMF分量c1(t)与 c2(t)分别对应于原始信号的合成分量x2(t)与x1(t)，它们之间的比较在图6中给出，从中可以看出基于折线包络的EMD方法分解所得到的IMF分量与原始信号合成分量的符合程度是非常好的。其中，c1(t)与x2(t)之间的比较是在区间[1.0,2.0]中给出的，其他区间二者的吻合程度与该区间类似。

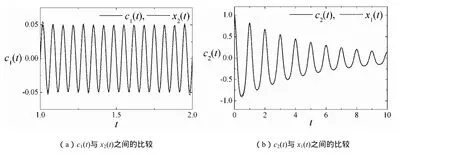
图6 基于折线包络EMD方法分解x(t)所得主要IMF分量与x(t)的合成分量之间的比较Fig. 6 Comparison between the main IMF components obtained by using folding-line-envelope-based EMD decompose x(t) and the synthesizing components of x(t)

对图5所示IMF分量进行Hilbert谱分析之后，可得到原始信号的Hilbert谱，如图7所示。其中，频率保持在15.0Hz的高频分量为原始信号中的高频噪声部分x2(t)，其谱值非常低；频率在1.0Hz波动的分量为原始信号中的余弦调频波，其谱值随时间衰减。针对该图有两点需要说明：①由于离散Hilbert变换与数值微分所带来的误差，低频分量瞬时频率只是大体上遵循式（11）所示的余弦变化；②由于在进行Hilbert谱分析时沿时间轴进行了平滑处理，以及数值计算所导致的瞬时频率微小的波动，使得这两个分量在其瞬时频率附近均出现了较窄的频带。

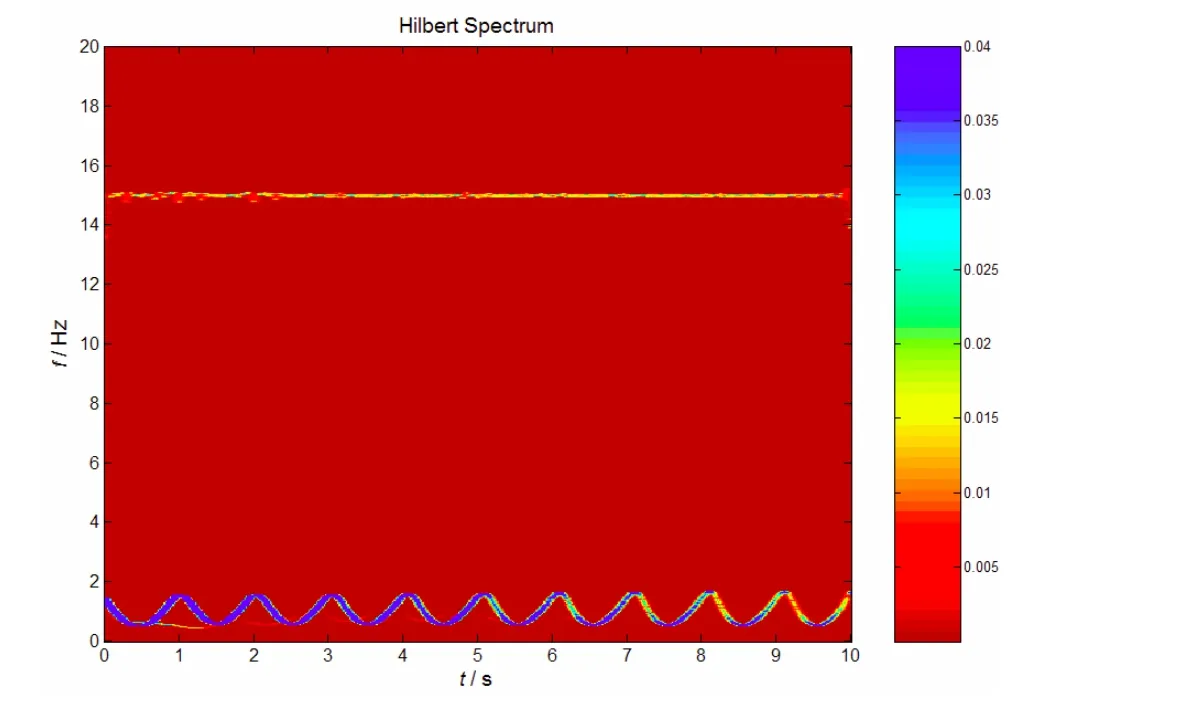
图7 原始信号的Hilbert谱Fig. 7 Hilbert spectrum of original signal

2.2 地震动加速度记录

图8 给出的波形为1940年美国El Centro强震加速度记录。应用基于折线包络EMD方法分解该记录所得的IMF分量及每个IMF分量所对应的Fourier幅值谱，如图9所示。从图9（a）、图9（c）中可以看出：①所有分量的波形都对称于零轴；②每个分量波形的所有极大值点均位于零轴以上，所有极小值点均位于零轴之下。因此该方法分解El Centro波所得到的分量满足IMF的要求，此外每个IMF分量的波形还具有类似于窄带波包的特性。从图9所示IMF分量的波形与Fourier幅值谱中可以看出：每个IMF分量均代表着一种振动模态，它们的幅值与频谱含量各不相同，自第一个分量起，IMF分量的高频成分逐步减少。

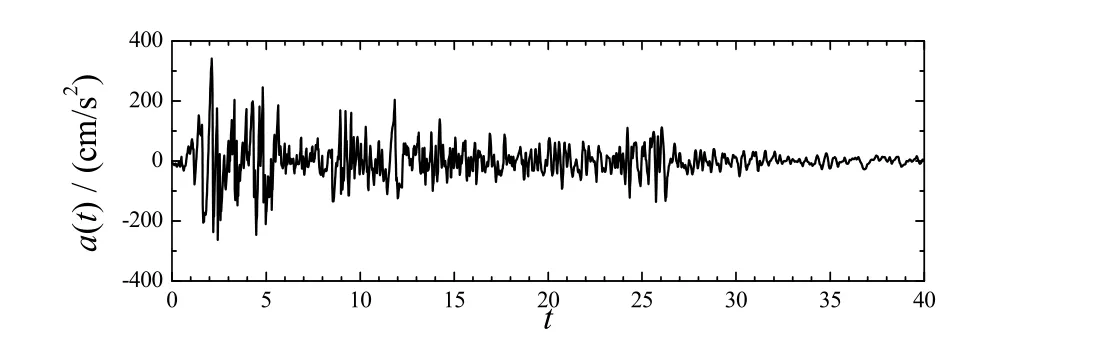
图8 El Centro地震加速度记录Fig. 8 Acceleration records obtained at El Centro station

对图9所示IMF分量进行Hilbert谱分析，可得到原始El Centro波的Hilbert谱，如图10所示。从中可以看出，地震动的Hilbert谱揭示了原始地震动的能量在时间-频率域上的分布特征，与时间-频率反应谱有相同的作用，对于研究地震动的工程特性具有重要意义（罗奇峰等，2003）。而且，相比小波谱，与原始EMD方法所得结果相似，本文提出基于折线包络的EMD所得地震动Hilbert谱同样具有更高的时频分辨率（Huang等，1998）。

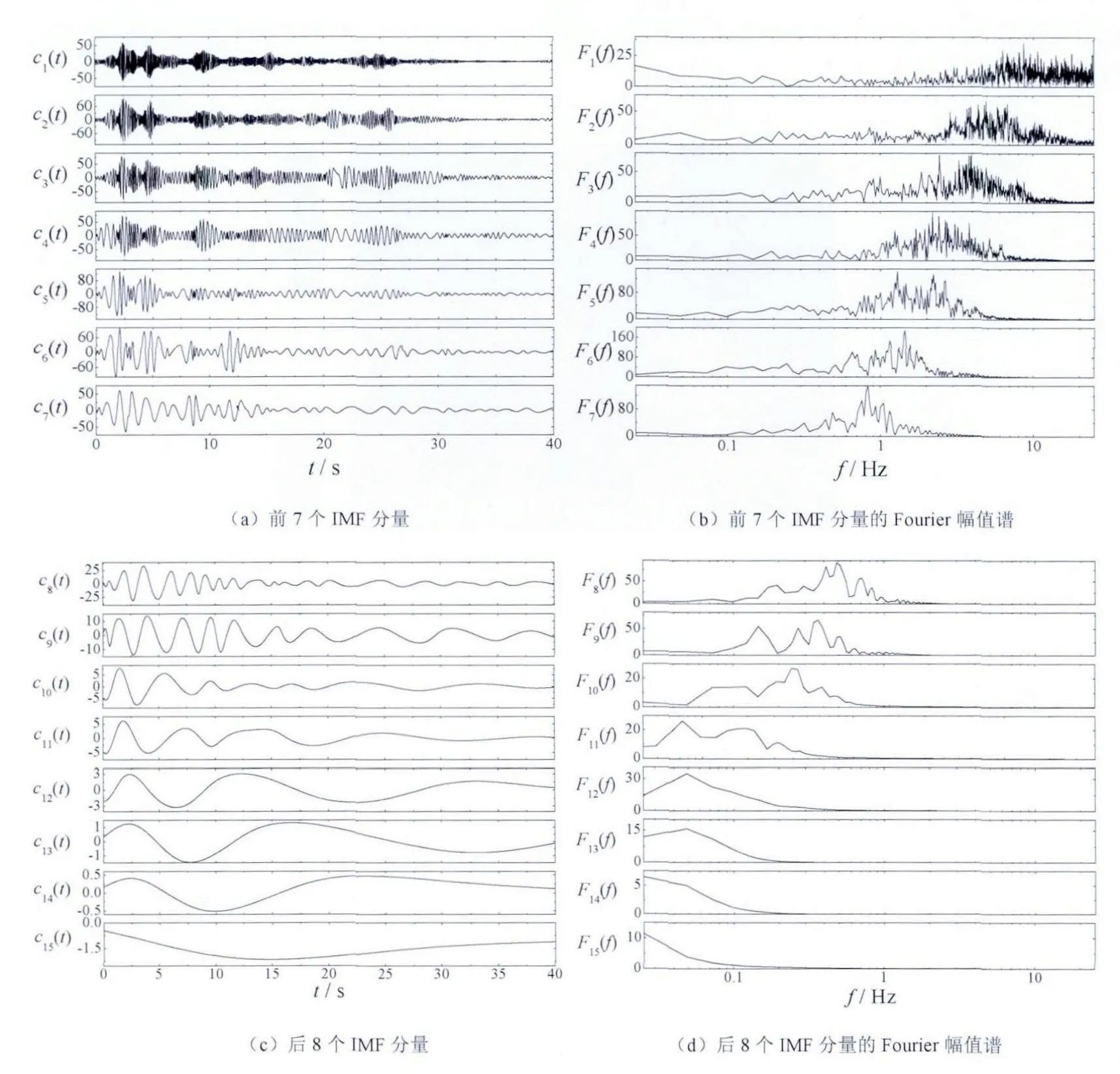
图9 基于折线包络的EMD方法分解El Centro波所得到的IMF分量及其Fourier幅值谱Fig. 9 The IMF components and the Fourier spectra of El Centro wave decomposed by the folding-line-envelope-based EMD method

3 结论

本文针对原始的经验模态分解方法处理长周期信号所面临的问题，提出了一种基于折线包络的经验模态分解方法，通过对比两者对信号“筛分”处理过程，论证了基于折线包络EMD方法的分解效率，以一个具有明确解析表达式的信号为例验证了该方法所得结果的数学意义，并且分析了该方法分解 El Centro波所得 IMF分量的频谱特性以及所得到的Hilbert谱的特征。

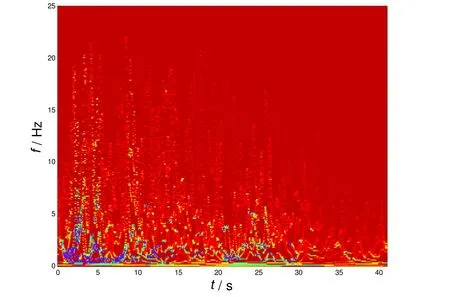
图10 El Centro波的Hilbert谱Fig. 10 The Hilbert spectrum of El Centro wave

邓拥军，王伟，钱成春等，2001. EMD方法及Hilbert变换中边界问题的处理. 科学通报，46（3）：257—263.

黄大吉，赵进平，苏纪兰，2003. 希尔伯特-黄变换的端点延拓. 海洋学报，25（1）：3—6.

罗奇峰，石春香，2003. Hilbert-Huang变换理论及其计算中的问题. 同济大学学报，31（6）：637—640.

石春香，罗奇峰，施卫星，2005. 基于Hilbert-Huang变换方法的结构损伤诊断. 同济大学学报（自然科学版），33（1）：17—20.

张郁山，梁建文，胡聿贤，2003. 应用自回归模型处理EMD方法中的边界问题. 自然科学进展，13（10）：1054—1059.

Huang N.E., Shen Z., Long S.R. et al., 1998. The Empirical Mode Decomposition and Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis. Proc. Roy. Soc. Lond., A (454)∶ 903—995.

Huang N.E., Shen Z. and Long R.S., 1999. A New View of Nonlinear Water Waves—Hilbert Spectrum. Ann. Rev.Fluid Mech., 31∶ 417—457.

Huang N.E. et al., 2001. A New Spectral Representation of Earthquake Data∶ Hilbert Spectral Analysis of Station TCU129, Chi-Chi, Taiwan, 21, September 1999. Bull. Soc. Seism. Am., 91 (5)∶ 1310—1338.

Loh C.H., Wu T.C. and Huang N.E., 2001. Application of the Empirical Mode Decomposition—Hilbert Spectrum Method to Identify Near-fault Ground Motion Characteristics and Structural Responses. Bull. Soc. Seism. Am.,91 (5)∶ 1339—1357.

Pines and Salvino L.W., 2001. Health Monitoring of Structures Using Empirical Mode Decomposition and Phase Dereverberation. See∶ Proc the 2001 Mech and Materials Summer Conf. UCSD∶ San Diego, CA∶ 228—229.

Salvino L.W., 2000. Empirical Mode Analysis of Structural Response and Damping. See∶ Proc the 18th Inter Modal Analysis Conf, San Antonio, TX∶ 503—509.

Yang J.N., Lei Y., Pan S.W. et al., 2003a. System Identification of Linear Structures Based on Hilbert- Huang Spectral Analysis. Part 2∶ Complex Modes. Earthq. Engrg. Struct. Dyn., 32∶ 1533—1554.

Yang J.N., Lei Y., Pan S.W. et al., 2003b. System Identification of Linear Structures Based on Hilbert- Huang Spectral Analysis. Part 1∶ Normal Modes. Earthq. Engrg. Struct. Dyn., 32∶ 1443—1467.

Yang J.N., Lei Y., Lin S. et al., 2003c. Hilbert-Huang Based Approach for Structural Damage Detection. J. Engrg.Mech., ASCE, 130 (1)∶ 85—95.

Zhang R.R., Ma S., Safak E. et al., 2003. HHT Analysis of Earthquake Recordings. J. Engrg. Mech., ASCE, 129 (8)∶861—875.

Zhang Y.S., Liang J.W. and Hu Y.X., 2005. Hilbert Spectrum and Intrinsic Oscillation Mode of Dynamic Response of a Bilinear SDOF System∶ Influence of Harmonic Excitation Amplitude. Earthq. Engrg. Engrg. Vibr., (1)∶17—26.