由不同生成元而形成的Cantor集的多重分形谱比较
左 飞 (盐城师范学院数学科学学院,江苏 盐城 224002)
由不同生成元而形成的Cantor集的多重分形谱比较
左 飞 (盐城师范学院数学科学学院,江苏 盐城 224002)
为了研究在不同生成元下,Cantor集的多重分形谱的变化规律及比较它们之间的差别。选择了Cantor集的一种质量分布,当赋予质量以不同的概率比时,用多重分形谱的方法加以分析,并用Matlab软件画出多重分形谱随奇异指数变化的函数图,能够直观的比较多重分形谱之间的差别和广义分形维数之间的差别。通过比较,当生成元之间的差别越来越小时,多重分形谱的宽度则越来越窄,且广义分形维数的纵向高度也越来越窄。所有多重分形谱的最大值均为Cantor集的Hausdoff维数,也即0.631。
分形几何;多重分形测度;多重分形谱;广义分形维数;Cantor集
多重分形测度理论为近年来分形几何研究的一个重要而活跃的分支,特别是对于统计物理学而言,因为单一的分形维数只能反映不规则对象的总体特征,不能对分形对象作更细微的分析,因此对于刻画客观事物的形貌显得越来越‘粗糙’。而多重分形理论对不规则研究对象内部之间赋予概率的成分,充分考虑到不规则对象内部各区域之间的分布的不均匀性,从而更细致的刻画了分形几何对象的特征。下面,笔者从多重分形测度理论的角度来分析典型的分形集Cantor集的多重分形谱与广义分形维数。
1 主要概念与结论
定义1[1-2](多重分形测度) 设μ为定义在Rn上的测度,且0<μ(Rn)<∞,若满足幂律关系式:
μ(Br(x))∝rα
(1)
式中,Br(x)为以x为中心、r为半径的闭球;α为幂指数(也称奇异指数),则称具有这种性质的分布或测度称之为多重分形测度。
定义2[1-3](配分函数、质量指数) 对于尺度为δ的盒子,其第i个盒子的质量分布概率为Pi(δ),称表达式:
(2)
为配分函数。由式(2)两边取对数,再取极限得到:
(3)
τ(q)称为质量指数。
定义3[1-3](广义分形维数) 定义广义分形维数Dq为:
(4)
定义4[1-3](多重分形谱) 设F是一个分形集,用尺度为δ的盒子对F进行划分,把全部概率分布为Pi(δ)组成的集划分为一系列子集,即按Pi(δ)的大小划分为满足下面的幂函数的子集:
Pi(δ)∝δα
(5)
这里α为奇异指数(它是反映分形上各个小集合的奇异程度的一个量,所以α的数值必定与所在的子集有关。特别地,如果分形集F分布是均匀的,则α必然只有一个值。若不均匀,可以用α值的大小区分为许多小子集)。将子集内的单元数N(δ)和δ的关系定义为:
N(δ)∝δ-f(α)
(6)
这里的f(α)就表示具有相同奇异指数α的子集的分形维数。称f(α)为多重分形谱。它是奇异指数α的函数。
经过证明[1-2],q(-∞ (7) 如果已知质量指数τ(q),则可以求出奇异指数α(q),式(7)给出了多重分形谱f(α)的参数表达式,参数为q。另一方面,如果能测得广义分形维数Dq,可以计算奇异指数α(q),然后计算出τ(q),从而由式(7)计算出f(α)。相反如果已知f(α),由此得到q,再求出τ(q),最后由式(4)求出Dq。它们之间都是隐函数和参量方程的关系,对于一般的分形集,以上多重分形理论是严格的,但在实际应用上计算非常困难,因此从应用角度出发,只能用近似的计算来逼近以上的理论。 这里定义多重分形谱的宽度[3]为: Δα=αmax-αmin (8) 它在图中的宽、窄程度定量的表征了分形曲线的各小区间中最大、最小概率间的差别。 (9) (10) 从而由式(7)可得多重分形谱为: (11) 下面取生成元为不同的值比较其差别: (1)当p1=1/8,p2=7/8,其多重分形谱与广义分形维数的图如图1、图2所示: D-∞=1.893D∞=0.122D1=f(α(1))=0.343=f(α(-1)) (2)当p1=1/6,p2=5/6,多重分形谱与广义分形维数的图如图3、图4所示: D-∞=1.631D∞=0.166D1=f(α(1))=0.410=f(α(-1)) (3)当p1=1/4,p2=3/4,多重分形谱与广义分形维数的图如图5、图6所示: D-∞=1.262D∞=0.262D1=f(α(1))=0.512=f(α(-1)) (4)当p1=1/3,p2=2/3,多重分形谱与广义分形维的图如图7、图8所示: D-∞=1D∞=0.369D1=f(α(1))=0.579=f(α(-1)) 图1 p1=1/8,p2=7/8的多重分形谱 图2 p1=1/8,p2=7/8的广义分形维数 图3 p1=1/6,p2=5/6的多次分形谱 图4 p1=1/6,p2=5/6 的广义分形维数 图5 p1=1/4,p2=3/4的多重分形谱 图6 p1=1/4,p2=3/4的广义分形维数 (5)当p1=2/5,p2=3/5,多重分形谱与广义分形维数的图如图9、图10所示: D-∞=0.834D∞=0.465D1=f(α(1))=0.613=f(α(-1)) (6)当p1=1/2,p2=1/2,多重分形谱与广义分形维数的图如图11、图12所示: D-∞=D∞=0.631 图7 p1=1/3,p2=2/3的多重分形谱 图8 p1=1/3,p2=2/3的广义分形维数 图9 p1=2/5,p2=3/5的多重分形谱 图10 p1=2/5,p2=3/5的广义分形维数 图11 p1=1/2,p2=1/2的多重分形谱 图12 p1=1/2,p2=1/2的广义分形维数 综上所述,简单分形维数(如盒维数),仅仅是对分形曲线形貌的总体表征,而并没有考虑曲线内部分布的不均匀性,因此对于刻画分形曲线显得比较“单一”,而多重分形理论以概率分布的方式,考虑了在分形曲线内部分布的不均匀性。多重分形谱的宽度Δα可以定量的说明分形曲线的起伏程度。 [1]Kenneth Falconer.分形几何的数学基础及其应用[M]. 第2版.曾文曲译.北京:人民邮电出版社,2007. [2]文志英.分形几何的数学基础及应用[M].上海:上海科技出版社,1999. [3]孙霞,吴自勤,黄畇.分形原理及其应用[M].合肥:中国科学技术大学出版社,2006. [4]Sha Zhen, Luan Huojun.Fractal and Fitting[M].Hangzhou:Zhejiang University Press,2005. [5]Chhabra A,Jensen R V.Direct dimension of thef(α) singularity spectrum[J]. Phys Rev Lett,1989,62(12):1237-1330. [6]Xie Heping, Wang Jin-an, Kwa niewski M A.Multifratacl characterization of rock fracture surfaces[J]. Int J of Rock Mechanics & Mining Sciences,1999,36: 19-27. [7]孙洪泉.分形几何与分形插值[M].北京:科学出版社,2011. [编辑] 洪云飞 O189 A 1673-1409(2013)25-0001-04 2013-06-24 左飞(1981-),男,硕士,讲师,现主要从事应用数学方面的教学与研究工作。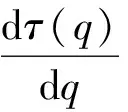
2 应用举例











3 结 语

