如何培养学生的“感知论证”能力——由学生“想不到”引起的反思与实践

●

(元济高级中学 浙江海盐 314300)

如何培养学生的“感知论证”能力——由学生“想不到”引起的反思与实践

●甘建飞

(元济高级中学 浙江海盐 314300)

1 问题的提出

长期以来，关于解决几何问题的2种论证方式：推理论证与感知论证，有着不小的争议.赞成推理论证的教师认为：解决几何问题应该从已知条件出发，通过层层推理，最终得到结论.赞成感知论证的教师认为：解决几何问题应该先“感知”可能的结论，然后再论证“感知”是否正确.“感知论证”使几何想象能力强的学生在解决问题时脱颖而出.但“感知论证”的教学也存在一个很大的困惑：教师很难去解释思维的起点(即如何想到).正因为“感知论证”的偶然性，最初笔者对“感知论证”也持谨慎态度.不过数年前的一堂立体几何课，引起了笔者的思考，在这几年作了不少尝试，现对此作一论述，希望各位同行批评指正.

2 课堂片断再现

(给出例题，学生开始思考……)

图1

例1如图1，在ABCD中，AB=2BC，∠ABC=120°，E为线段AB的中点，将△ADE沿直线DE翻折成△A′DE，使平面A′DE⊥平面BCDE，F为线段A′C的中点，设M为线段DE的中点，求直线FM与平面A′DE所成角的余弦值．

师:请一位同学说一下解题思路.

生1:过点F作平面A′DE的垂线，垂足为H，联结MH，则∠FMH就是所求直线与平面的所成角.但点H还没找到.

(大多数同学由于无法确定点H的位置，解题陷入困境.)

生2:等体积法应该能求出点F到平面A′DE的距离，但还没想好怎么算.

生3:由平面A′DE⊥平面BCDE可知，过点C作DE的垂线CN，则CN⊥平面A′DE，再在△A′NC中作A′N的平行线FH，就可以找到垂足H.

(学生进行了复杂的计算，其中部分学生虽然没有得到点N的精确位置，但计算得到了CN的长度，进而得到了所需的答案.)

师:得到答案的同学看看，点N的具体位置到底在哪里？

(学生通过数据比对，发现CN=CE，原来点N与点E重合!)

生4(很懊恼):我怎么就没去想想点E是不是就是垂足呢!其实刚开始就找准垂足，论证和计算是很容易的.

事实上，在课前的预设中，笔者认为这个问题的解决只需要5分钟左右.但在上课过程中，由于学生“想不到”点E就是垂足，问题的解决足足花了15分钟.课后笔者问过一些学生，当时怎么就没有想到点E就是垂足呢？有学生回答说，其实是想过这个可能，但认为不可能这么巧，也就没有去尝试“碰运气”.

课后经过整理，笔者在另一个班也上了这节课，发现整个过程大同小异，甚至加入了提示：“同学们可以先尝试空间问题平面化，研究一下ABCD.”大部分学生面对平面图形，还是没有去考虑点E这个特殊位置，学生们很默契地将上一节课的情形又重演了一遍.

显然，学生在几何的学习中，有一种推理论证的思维习惯，只能以推理论证后得到的结果，反过来去认识图形.而没有形成先对图形中的可能情形进行“感知”，进而去论证的习惯.因此，在解决课例中的问题时，显得力不从心.

从那时起，笔者开始了提高学生“感知论证”能力的尝试，在教学中充分挖掘各种教学元素(包括代数中的几何元素)，引导学生养成“感知论证”的思维习惯，帮助学生提高解决几何问题的能力.

3 前期教学提升学生“感知论证”能力的若干教学片断

3.1 平面向量教学中“感知论证”能力的培养

例2如图2，在ABCD中，AB=1，BC=2,M是BC的中点，求证：AM⊥DM.

图2

即AM⊥DM.

点评本例是平面向量的数量积在几何中的应用问题，考查如何用向量方法证明垂直.笔者通过教学，引导学生思考：

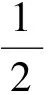
图3

(2)你能否通过上述结论，在类似问题的判断中摆脱“绝对位置”的干扰，只考虑它们的相对位置吗？

3.2 直线与圆教学中“感知论证”能力的培养

例3如图2，ABCD中，AB=1，BC=2,M是BC的中点.

(1)求证:AM⊥DM；

(2)试求∠ABC的取值范围，使除点M外，线段BC上还存在点N，使AN⊥DN.

图4

解(1)如图4，以AD为直径作圆，显然点M在以AD为直径的圆上，由直径所对圆周角为直角易得，∠AMD=90°，即AM⊥DM.

点评利用圆“直径所对圆周角为直角”验证是否垂直(或探索是否有垂直)，是圆作为解题工具的主要功能.特别适用于是否存在垂直关系的快速感知：若以AD为直径的圆与BC有2个交点时，则存在2个满足题意的点；若没有交点，则这样的点不存在.因此，引导学生“较精确”作图，并借助圆工具判断，可以使学生在立体几何学习时形成“空间问题平面化”的思维习惯，为立体几何的学习打下扎实的思维基础.

4 几点思考

4.1 前期“感知论证”能力的培养，为立体几何的学习打下了基础

美国教育心理学家奥苏贝尔认为，影响学习的最重要因素是学生已有的认知结构，他强调学生的学习应该是有意义的接受学习，这种学习是通过新知识与学生认知结构中的有关观念相互作用而进行的，其结果是新旧知识意义的同化.

而立体几何教学的突破，关键在于：(1)学生处理平面几何问题的能力，空间几何体是由基本的平面图形构成，在前期“感知论证”能力的培养后，学生的平面处理能力已经有了较大的提高，为立体几何的学习打下了基础；(2)“感知论证”的思维习惯，可以使立体几何的学习“事半功倍”.空间中的线面关系更为复杂，每一个关系都靠推理来论证，显然是不现实的.经过多年的教学观察，笔者发现很多学生立体几何的学习困境，很大程度上就是由于太过于执着每一个线面关系的论证.

4.2 “感知论证”能力的培养，更应注重垂直结构的“感知”

在“感知论证”的教学中，选取的素材大多与垂直有关.这主要基于两点：(1)在平面向量问题，直线与圆问题的学习中，教学的难点是非垂直问题，垂直问题是此类问题中较容易的问题，却是提高学生“感知论证”能力最好的素材.选择垂直问题，可以在不增加学生负担的前提下，更大限度地提升学生对原概念的理解.(2)垂直结构是立体几何的核心结构，后续的线面角、二面角等问题，都需要在垂直结构下解决，可以说，垂直结构感知能力的高低，很大程度上决定了学生的空间想象能力.

事实上，很多优秀的教师，往往在某一知识教学之前，就做好了学习这一知识所需能力的培养.而年轻教师由于缺少经验，往往只能被动地等学生陷入困境时才发现问题，但能力的生成不是一蹴而就的，等问题出现后再补救就来不及了.而从前期教学中合理选择几何元素进行“感知论证”能力的培养，可以使学生在学习原知识的同时，慢慢提高解决立体几何问题所需的能力,如此可以更好地实现知识体系的系统化，实现课堂的“轻负高质”.