一道自主招生试题的“前世后生”
●
(余姚市实验学校 浙江余姚 315400)
一道自主招生试题的“前世后生”
●陈万勇应立君
(余姚市实验学校 浙江余姚 315400)
随着全国高校自主招生的规模越来越大,引发各地高中的自主招生热,一批学有余力的资优生有了极佳的展示平台,而重点高中也多了一条发现人才的重要途径.从已有的自主招生数学试题分析可知,试题大多来源于竞赛题,或直接引用,或稍加改编,推陈出新.研究经典的竞赛试题,无异于挖掘了自主招生试题的源头,真可谓是事半功倍.下面是对2009年浙江省某重点高中自主招生试卷压轴题的“前世”挖掘与“后生”展望,以期抛砖引玉,对数学资优生的自主探究、辅导教师的有效指导及自主招生试卷的创新命题等有所借鉴.
1 试题的“前世”
例1如图1,四边形ABCD内接于圆,AB=AD,且其对角线交于点E,点F在线段AC上,使得∠BFC=∠BAD=2∠DFC.
(1)求∠CDF的大小;
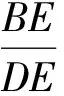
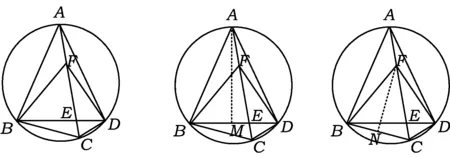
图1图2图3
分析此题实际应试时得分很低.时间紧张、精确作图困难是主要原因.好不容易猜想出正确结论,但推理过程又成了障碍.
此题蕴含着丰富的数学知识与思想方法:等腰三角形、灵活转化的圆周角、相似三角形、三角形的角平分线性质、演绎与归纳推理等,具有极高的研究价值.
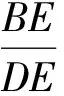
解(1)如图2,过点A作AM⊥BD于点M,则

因为∠ABD=∠ACD,所以
∠CDF=∠AMB=90°.
(2)如图3,过点F作FN⊥BC于点N.先证△FCN≌△FCD,得CN=CD;再证FB=FC,得BN=CN.因为CE是△BCD的角平分线,所以
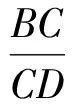
此题综合性强,解法巧妙,且解法众多(读者可再作探究),不失为一道好题,但感觉似曾相似.经查阅知,其来源于2008年青少年数学国际城市邀请赛中的一道试题:
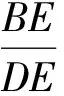
自主招生题增加了第(1)小题的设置,有暗示解法之意,降低了难度.再追溯,此题可以认为脱胎于1992年全国初中数学联赛中的一道解答题:
例3如图4,在△ABC中,AB=AC,D是底边BC上的一点,E是线段AD上的一点,且∠BED=2∠CED=∠BAC.求证:BD=2CD.
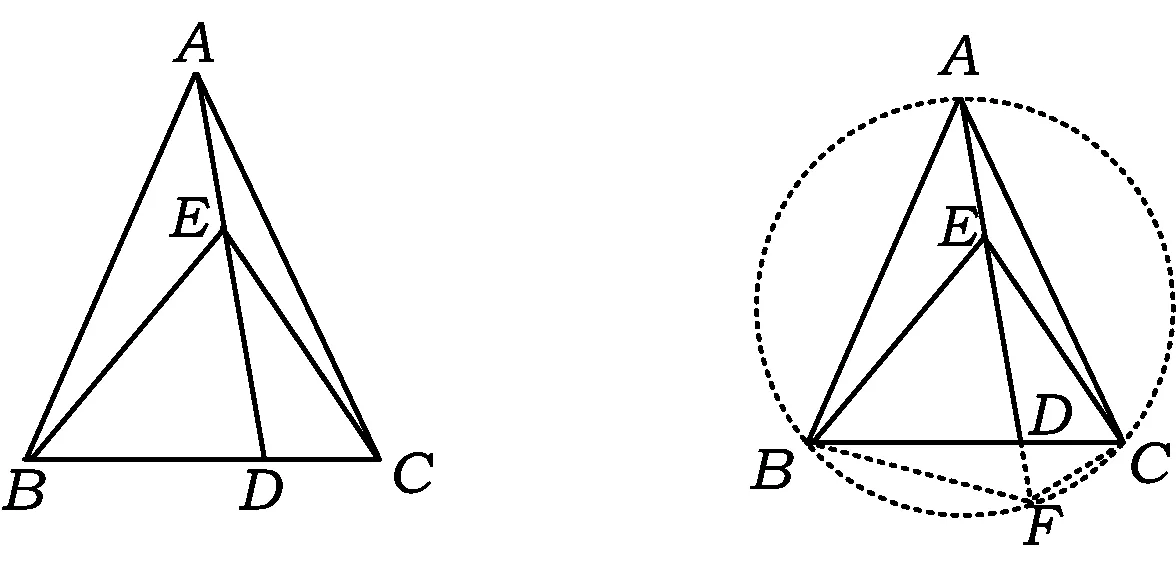
图4 图5
给图4披上圆的外套(如图5),延长AD交△ABC的外接圆于点F,联结BF,CF,则与例1、例2无异了.这是一种解法,例3还有很多解法,下面择取几种以飨读者:
证明先证明BE=2AE.如图6,在BE上截取BF=AE,联结AF,易证△ABF≌△CAE,得∠AFB=∠CEA,则

于是AE=EF,从而BE=2AE.
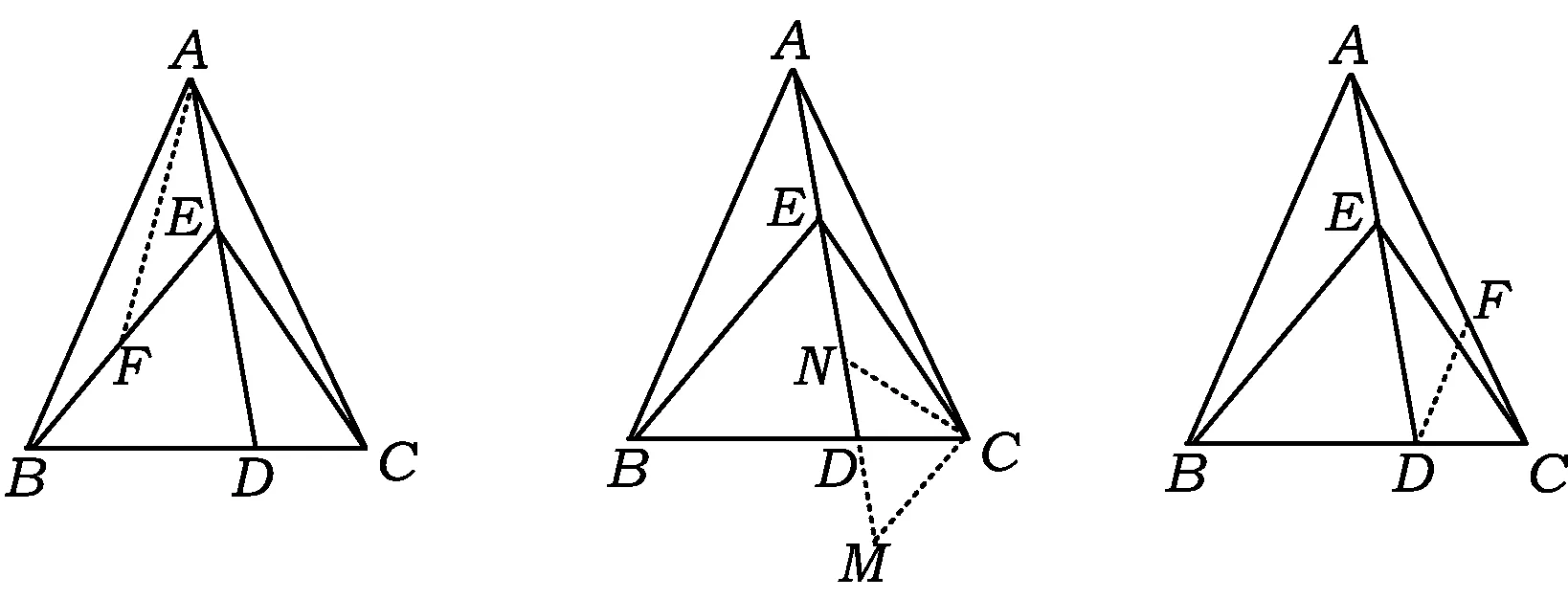
图6 图7 图8
方法1如图7,过点C作CM∥BE交AD延长线于点M,在AD上截取AN=BE,联结CN.
先证△ABE≌△CAN,得
CN=AE,∠CND=∠BED,
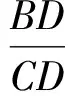
方法2如图8,过点D作DF∥AB交AC于点F,易知FC=FD.
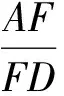
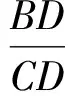
方法3如图4,在△ABE中,由正弦定理,得
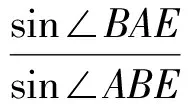
从而
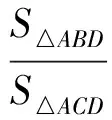
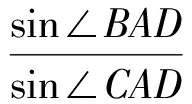
故
BD=2CD.
以上解法都用到了2个几何事实:∠ABE=∠CAD,BE=2AE,较之题干中的陈述条件更加有利于应用.
2 试题的“后生”
经过上述剖析,相信读者对蕴藏于这道试题之中的几何知识与思想方法已经相当地了解,那么以后的试题可以进行怎样的发展演变呢?笔者进行了如下的初步尝试:
2.1 互换条件与结论
如图4,已知△ABC中,AB=AC,D是BC上一点,BD=2CD,且∠ABE=∠CAD. 求证:∠BED=2∠CED.
2.2 增加条件,使图形特殊化
已知在△ABC中,AB=AC=1,D是BC上一点,E是线段AD上一点,且∠BAC=∠BED=2∠DEC.
(1)当∠BAC=90°时(如图9),求BD的长;
(2)当∠BAC=60°时(如图10),求△CDE的面积.
图9 图10
(解答留给读者.)
解题是数学学习的重要途径,需要我们全身心地投入其中,慢慢地品尝,体会各种美妙;认真细致地解剖,不同方向、角度地观察,创造性地链接尝试,以及解题成功以后的回望,不断促使解法完善,解答简化合理,发现多解,提炼通解,自拟试题等.日积月累,定会使解题功力大增,数学素养大幅提升.

