一道竞赛附加题的别证与推广

● ●

(衢州市第一中学 浙江衢州 324000)> (衢州市第二中学 浙江衢州 324000)

一道竞赛附加题的别证与推广

●李盛●杨樟松

(衢州市第一中学 浙江衢州 324000)> (衢州市第二中学 浙江衢州 324000)

2013年浙江省高中数学竞赛的附加题是一道不等式证明题：

题目设a,b,c∈R+,ab+bc+ca≥3,证明：

(1)

参考答案是利用幂平均值不等式进行证明的.注意到当a=b=c=1时，已知条件中的不等式等号成立，这启发了笔者利用算术—几何平均值不等式进行证明.笔者给出2种简单的证明方法，并将结论推广到一般情形.

1 赛题别证

证法1式(1)等价于

(a3+b3+c3)(a2+b2+c2)≥9.

由于a2+b2+c2≥ab+bc+ca≥3,只要证明a3+b3+c3≥3.利用算术—几何平均值不等式

a3+a3+1≥3a2,b3+b3+1≥3b2,c3+c3+1≥3c2,

3个不等式相加，得

2(a3+b3+c3)+3≥3(a2+b2+c2)≥9,

即a3+b3+c3≥3，结论显然成立.

证法2同证法1，只要证明a3+b3+c3≥3.利用算术—几何平均值不等式

a3+b3+1≥3ab,b3+c3+1≥3bc,c3+a3+1≥3ca,

3个不等式相加，得

2(a3+b3+c3)+3≥3(ab+bc+ca)≥9,

即a3+b3+c3≥3，结论成立.

2 赛题推广

不等式(1)可以推广到更一般的情形：

推广设a,b,c∈R+,ab+bc+ca≥3,n≥1,m≥1,则

(2)

证明因为(a+b+c)2≥3(ab+bc+ca)≥9,所以a+b+c≥3.同时，n≥1,m≥1,利用幂平均值不等式，得

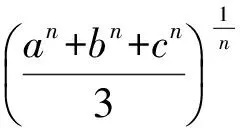
故an+bn+cn≥1.同理am+bm+cm≥1，从而

(an+bn+cn)(am+bm+cn)≥3×3=9，

(3)

式(3)与式(2)等价.

3 问题引伸

命题1设a,b,c∈R+,ab+bc+ca≥3,n≥1,则an+bn+cn≥1.

此结论在上面的推广证明中已证.

命题2设ai>0(i=1,2,…,n)，1k,且

a1a2…ak+a2…akak+1+…+ana1…ak-1≥n,

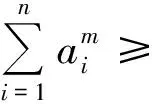
证明由算术—几何平均值不等式，得

……

将这n个不等式相加，得

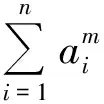
即命题2成立.

对于an+bn+cn和am+bm+cm的大小关系，有以下结论:

命题3设a,b,c∈R+,ab+bc+ca≥3,n-1≥m≥1,则

证明利用切比雪夫不等式，得

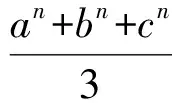
(5)

由于n-m≥1,根据命题1，知an-m+bn-m+cn-m≥3.至此，式(5)等价于式(4).

如果将条件n-1≥m≥1改为n≥m≥1，能得到什么结论？

命题4设a,b,c∈R+，aabbcc>1,n≥m≥1,则

证明当a=b=c=1时，不等式(6)显然成立；当a,b,c不全为1时，不等式(6)成立等价于函数f(x)=ax+bx+cx在x∈[1,+∞]上是增函数.因为

f′(x)=axlna+bxlnb+cxlnc,x∈[1,+∞)，

则

f″(x)=ax(lna)2+bx(lnb)2+cx(lnc)2>0,

所以f′(x)是[1,+∞)上的增函数，故

f′(x)≥f′(1)=alna+blnb+clnc=lnaabbcc>0.

因此，不等式(6)成立.

第九届全国初等数学研究及中学数学教育教学研讨会征文通知

第九届全国初等数学研究及中学数学教育教学研讨会由全国初等数学研究会举办，合肥师范学院承办，拟于2014年7月31日～8月3日在安徽省合肥市举行(具体会议时间以正式会议通知为准)。

1.征集论文(未经发表)内容：初等数学专题研究的新成果或某一专题研究综述；中学数学教育教学研究；数学自主招生、数学竞赛与竞赛数学研究；中、高考试题研究；数学文化。

2.有关奖项：评选和颁发第五届“中国中青年初等数学研究奖”(名额5人)；评选第三届中国“初等数学研究成果奖”；会议将评选第三届中国“初等数学研究杰出贡献奖”(原则上不超过2人)。申报条件和要求详见全国初等数学研究会网站，参评者请联系杨学枝理事长(手机13609557381)，将以上材料的word电子文稿最迟在2014年3月31日发送杨学枝理事长(邮箱yangxuezhi1121@126.com)。

3.投稿要求：来稿具体行文格式、要求详见全国初等数学研究会网站。发送论文时，请另附一份作者简介，作者的详细通讯地址、邮政编码、联系电话(最好是手机号码)、电子邮箱等word电子文稿。稿件请用word电子文件发送E-mail至cgcs1314@yeah.net，同时将论文评审费50元汇至中国建设银行：江嘉秋 4367 4218 2321 0109 448,汇款时一定要注明作者姓名、工作单位和相关事项。汇款后务请发短信至江嘉秋(手机 13705936996)，否则不予评审。

4.相关事宜：全国初等数学研究会网站地址：http://www.cdmath.org;邀请部分优秀论文作者参加本届会议；部分优秀论文将安排在全国初等数学研究会会刊《中国初等数学研究》杂志上发表；会议详情与信息请关注全国初等数学研究会网站；向大会提交论文的最后期限是2014年3月31日，逾期不予受理。

全国初等数学研究会

2013年3月1日