巧用函数的性质和图像速解、智解数学题
●
(青田县教育局 浙江青田 323900)
巧用函数的性质和图像速解、智解数学题
●高歌
(青田县教育局 浙江青田 323900)
考试是“对”、“错”的较量,“快”、“慢”的竞技.在考试规定的时间内,又“对”又“快”地完成考题、选准答案,实现单位时间内答题成功的最大效应,是我们孜孜以求的愿望和永恒不变的追求!在数学高考坚定不移地坚持“考查基础知识的同时,注重考查能力”的原则,确立“以能力立意命题”的指导思想,着力实现“多想少算”的思想理念,在“考基础、考能力、考智慧”等方面下功夫,将“知识、能力和素质”融为一体.在全面检测考生数学综合素养的大背景下,如何提高数学解题方法的多样性、灵活性与变通性,提升解题的技术能力与策略水平,显得尤为重要!
笔者认为,在日常教学中,教师应当在掌握“数学基本知识、基本技能和基本思想方法以及通性通法”的基础上,注重解题技能的训练,数学解题要力求“强攻”和“轻取”并举、“通法”和“巧法”并重,着力优化算理算法,不断提升解题技法.教师不仅要“会算,会少算,会巧算、简算、估算”,也要“会速算,会心算,会智算”,乃至“会不算”就能破解数学问题,以致使数学解题步入“对而快,快而对”的艺术境界.本文简单地阐述如何以超然的视角与独到的眼光,巧妙运用函数的性质特点与图像特征,迅速求解数学考题,从而大幅提高数学解题的“速度”与“效率”.
1 巧用函数定义域,速解与智解数学考题
“函数的定义域”是函数的重要组成部分,是构成函数的2个基本条件之一(另一个基本条件是函数的“对应法则”),是函数的“三要素”之一.一些函数的定义域有着明显的性质特征,如:由于奇函数的图像关于原点对称,偶函数的图像关于y轴对称,因此奇、偶函数的定义域必定关于原点对称;由于函数y=f(x)与其反函数y=f-1(x)在同一直角坐标系中的图像关于直线y=x对称,因此反函数y=f-1(x)的定义域就是其原函数y=f(x)的值域等等.一旦明白了奇、偶函数的定义域以及互为反函数的性质特征,便能“一举破解”乃至“一眼望穿”与之相关的数学考题.

( )
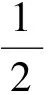
(2011年辽宁省数学高考文科试题)
分析本题主要考查奇函数的定义以及相应的变换运算、灵活运用能力.一般的解法是运用奇函数的定义,即:由函数f(x)为奇函数,知f(-x)=-f(x)对定义域内所有的x恒成立,从而

即-x(2x+1)(x-a)=-x(-2x+1)(-x-a),

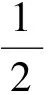
2 巧用函数的值域,速解与智解数学考题
“函数的值域”也是构成函数的“三要素”之一.事实上,函数的定义域和对应法则(即构成函数的2个基本条件)一经确定,函数的值域也就随之确定.对于有些题型(如选择题),若能巧妙地利用函数的值域,只要“简算”(“估算”),不要“详算”(“精算”);只要“动脑”(“心算”),不要“动手”(“笔算”),便能快速而准确地找到正确答案.
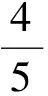
( )
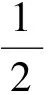
(2010年全国数学高考课标卷理科试题)
分析本题主要考查三角恒等变换中倍角公式的灵活运用、同角三角函数关系等知识以及相应的运算能力.若用“算到底”的思路求解,可能会采用以下4种解法.
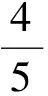
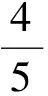
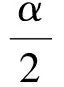
故
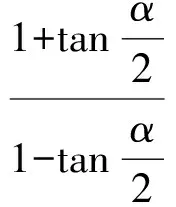
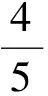

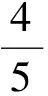
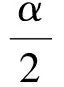
从而
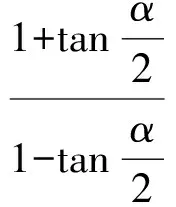
速解与智解1因为α是第三象限的角,则
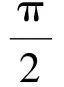
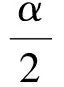
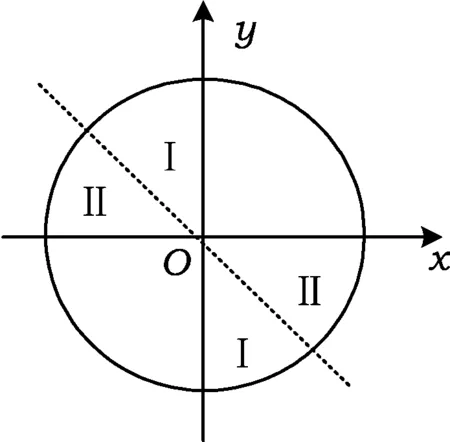
图1
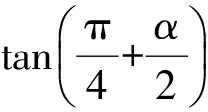
3 巧用函数奇偶性,速解与智解数学考题
函数的奇偶性是函数的重要性质之一,其特点是奇偶性函数的图像具有某种整体对称性:奇函数的图像关于原点对称,偶函数的图像关于y轴对称.在这些对称性中隐含着重要的数学结论,巧妙运用奇、偶函数的这些对称性及其蕴含的重要结论,往往可以使许多复杂的求解变得简单.
例3设偶函数f(x)满足f(x)=x3-8(x≥0),则{x|f(x-2)>0}=
( )
A.{x|x<-2或x>4} B.{x|x<0或x>4}
C.{x|x<0或x>6} D.{x|x<-2或x>2}
(2010年全国数学高考课标卷理科试题)
分析本题主要考查偶函数的性质、不等式的解法以及相应的运算能力.直接求解可能采用以下2种解法.
解法1当x<0时,-x>0,得
f(x)=f(-x)=-x3-8,
于是
则
令f(x-2)>0,得x>4或x<0.故选B.
解法2当x≥2时,
f(x)=x3-8>0,
解得
x>2.
因为f(x)是偶函数,所以当x∈R时,f(x)>0的解集为{x|x<-2或x>2}.又因为函数f(x)向右平移2个单位就得到函数f(x-2),所以f(x-2)>0的解集为{x|x<0或x>4}.故选B.
实际上本题并不需要这样一步一步来求解,利用偶函数的对称性就可以一步到位.
速解与智解由于偶函数f(x)的图像关于y轴对称,则不等式f(x)>0的解集也关于y轴对称,因此不等式f(x-2)>0的解集关于直线x=2对称,据此只能选择B.
4 巧用函数单调性,速解与智解数学考题
“函数的单调性”是函数的又一个重要性质,函数的单调性直观地呈现出函数图像增减变化的特点.有效地运用函数的单调性,可以快速地比较函数值的大小关系.尤其值得注意的是,利用函数的单调性可以把复杂的不等式求解、不等式证明以及比较大小等问题“转化”与“化归”为较简单的不等问题来处理.
例4如果cos5θ-sin5θ<7(sin3θ-cos3θ),θ∈[0,2π),那么θ的取值范围是______.
(2011年全国高中数学联赛试题)
分析本题一般的求解方法是先“移项”,得
cos5θ-sin5θ+7(cos3θ-sin3θ)<0,
再对左边式子“因式分解”来处理.但依据高中学生的知识基础,对左边式子的因式分解有一定的难度(即使能分解,其过程也相当复杂).但如果通过适当的变形,发现其为某一函数的变换,利用其单调性便可轻松破解.
速解与智解由已知,得
cos5θ+7cos3θ “函数的图像”是函数性质的直观体现,其最大的作用是让我们清晰地看到了函数的具体变化情况.在平常解决数学问题时,要注意把“数量关系”与“图形图像”联系起来,要注重对函数图像的把握与运用,从而使问题变得更加直观.事实上,“数形结合,以形助数”是一种极其重要的思想方法,更是一种重要的解题策略,利用函数的图像往往使有关问题的求解变得“直观而清晰、自然而便捷”. ( ) A.(-1,0)∪(0,1) B.(-∞,-1)∪(1,+∞) C.(-1,0)∪(1,+∞) D.(-∞,-1)∪(0,1) (2010年天津市数学高考理科试题) 分析本题主要考查函数求值、不等式求解、对数函数的单调性、对数的基本运算等基础知识,并考查分类讨论的数学思想.其一般的求解是用“分类讨论”的方法: 当a>0时,由f(a)>f(-a),得 即 则 解得 a>1. 当a<0时,由f(a)>f(-a),得 即 则 解得 -1 故选C. 若先画出该分段函数的图像,由函数图像的直观性,答案便立竿见影(还可以用“特殊值法”). 图2 速解与智解利用“数形结合”的思想,先画出函数的图像(如图2),则函数的内部结构及变换特征便“一览无余”,由图像便可选定C为正确答案. “函数”是描述客观世界变化规律的重要数学模型,“函数的思想方法”贯穿在整个高中数学课程的始终,“函数内容”也是高考数学的重要组成部分,在每年高考中都占有相当大的比重.我们要善于巧妙利用函数的诸多性质及其图像特征,使之成为快速而有效破解有关数学问题的一把“利剑”! [1] 蒋海瓯.关于试卷讲评的“点滴见解”[J].中学数学教学参考:上旬,2012(5):51-54. [2] “2010年高考:数学答题中的优美解及典型失误”证文选登(二)[J].中学数学教学参考:上旬,2010(8):38-53.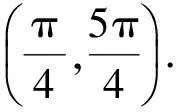
5 巧用函数的图像,速解与智解数学考题