一道猜想不等式的简证

●

(杭州市普通教育研究室 浙江杭州 310006)

一道猜想不等式的简证

●王红权

(杭州市普通教育研究室 浙江杭州 310006)

宋庆老师在文献[1]提出了一个不等式猜想如下：

猜想1若a，b，c是满足a+b+c=1的正数，求证：

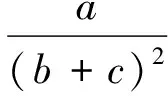
杨晋老师在文献[2]对猜想1进行了如下推广：

猜想2已知x1，x2，…，xn(n≥2)均为正实数，且x1+x2+…+xn=1，m∈N+，m≥2，证明或否定：

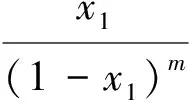
笔者发现当n=3，m=2时，不等式(2)并非不等式(1)，猜想系作者笔误．本文修正不等式(2)如下．

猜想3已知x1，x2，…，xn(n≥2)均为正实数，且x1+x2+…+xn=1，m∈N+，m≥2，证明或否定：

下面先给出不等式(1)的一个十分简单的证明，再证明猜想3是正确的．

1 猜想1的简证

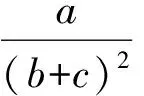
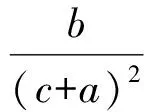
从而不等式(1)可转化为

注记上述对猜想1的证明简单通俗，从证明过程中可以得到，不等式(1)可以看作是Nesbitt不等式的一个推广．

2 猜想3的证明

引理1已知a，b均为正实数，且a+b=1，m∈N+，m≥2，则

证明根据二项式定理，有

两边同乘以a，得

再两边同除以bm，即得

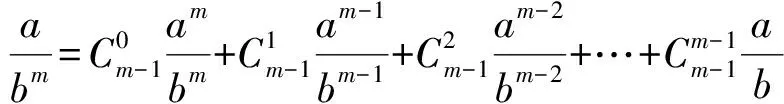
引理2[3](幂平均不等式)设x1，x2，…，xn均为正数，且有α≥β>0，则

证明(1)根据Cauchy-Schwarz不等式，得

从而

(2)根据引理2，有

下面证明猜想3：

证明由题意x1+(x2+…+xn)=1.根据引理1，得

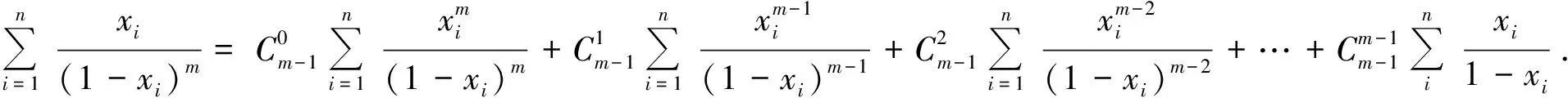
根据引理3，得

故猜想3成立．

[1] 宋庆，周芽瑜．关于证明不等式的一些思考[J]．中学数学研究，2012(2)：33-35.

[2] 杨晋．关于两道猜想不等式的简证[J]．中学数学教学，2012(5)：62-63.

[3] 匡继昌．常用不等式[M]．济南:山东科学技术出版社，2004：38.