2个竞赛不等式的统一证明
2013-10-26 01:04
中学教研(数学) 2013年7期
●
(常熟市中学 江苏常熟 215500)
2个竞赛不等式的统一证明
●査正开
(常熟市中学 江苏常熟 215500)
2012年爱尔兰国家奥林匹克数学竞赛中有2个不等式证明题,应用常规的不等式证明方法处理均需一定的技巧,对实施新课程后的学生来说有较大的难度.为此笔者采用“函数法”(文献[1])给出它们统一的简洁证明,以便使广大学生能很好地掌握.
例1若x,y∈R+,则(x+y)5≥12xy(x3+y3);并证明式中系数12是最佳的,即证明:对任意k>12都存在正实数x,y满足(x+y)5 (2012年爱尔兰国家数学奥林匹克竞赛试题) x2+y2=4xy, 于是 (2012年爱尔兰国家数学奥林匹克竞赛试题) 当0 当且仅当b=c时,上式等号成立,于是当且仅当a=b=c时,f(a)取到最小值0,因此 上述2个不等式均采用“函数法”理念,借助导数,通过讨论函数的单调性并求出最值完成对不等式的证明,这样可规避传统不等式证明中灵活多变的方法和高难技巧,使解题有明确的指向和固有的定式,思维流畅自然,很多复杂的不等式问题都迎刃而解,具有较广泛的适用性.这样处理不等式问题既适应新课程“降低不等式证明要求,强化函数(导数)的应用”的需求,又迎合“淡化特殊技巧,注重通性通法”的新高考理念,且符合学生的认知规律,能有效提高学生的思维能力和解题能力,激发学生的数学兴趣,促进数学的高效学习,值得在教学中加以推广和运用. [1] 査正开.自主招生数学试题中用“函数法”求不等式问题[J].中学教研(数学),2012(9):39-41.
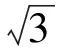
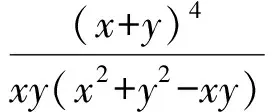

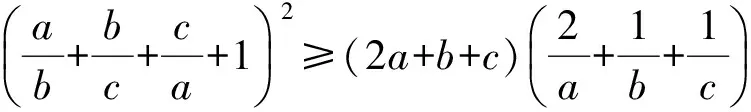
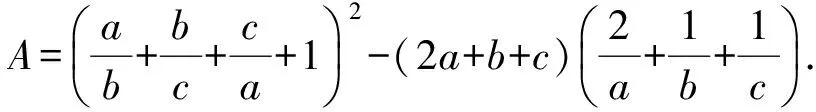


猜你喜欢
少先队活动(2022年9期)2022-12-16
阅读(快乐英语高年级)(2022年10期)2022-11-08
阅读(快乐英语中年级)(2022年9期)2022-10-08
少先队活动(2021年3期)2021-06-11
作文·小学中高年级(2021年12期)2021-05-18
作文·小学低年级(2021年12期)2021-02-03
英语文摘(2020年4期)2020-07-28
中国自行车(2017年1期)2017-04-16
小雪花·成长指南(2016年1期)2017-02-13
小雪花·成长指南(2016年3期)2016-04-20

