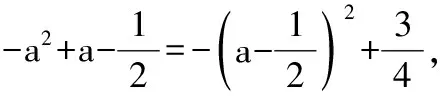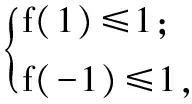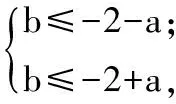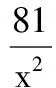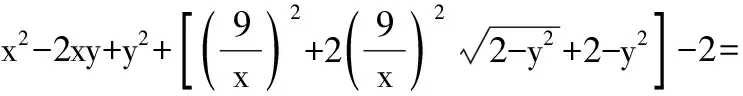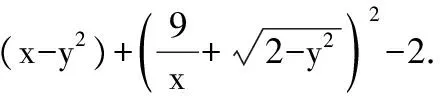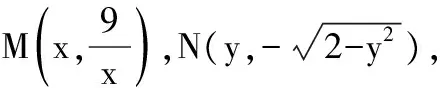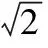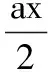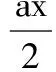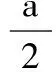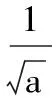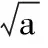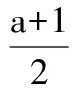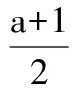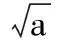含参数的恒成立问题

● (杭州市第二中学 浙江杭州 310053)

含参数的恒成立问题

●张先军(杭州市第二中学 浙江杭州 310053)

1 考点回顾

恒成立条件下不等式参数的取值范围问题，涉及的知识面广，问题的综合性比较强，解法比较灵活，渗透着换元、化归、数形结合、函数与方程等思想方法，考查学生数学思维的深刻性与敏捷性，从而成为高考的热点之一.笔者对此类问题的解决策略加以归纳，可加强学生知识体系的综合，有助于培养学生的数学思维，提高学生分析问题和解决问题的能力.

2 典例剖析

2.1 利用子集关系求解

例1设函数f(x)=a2lnx-x2+ax，a>0.

(1)求f(x)的单调区间；

(2)求所有的实数a，使e-1≤f(x)≤e2对x∈[1,e]恒成立．

注：e为自然对数的底数．

(2011年浙江省数学高考文科试题)

分析第(2)小题中只需满足y=f(x),x∈[1,e]的值域是集合[e-1,e2]的子集即可说明所有x∈[1,e]的值能使得e-1≤f(x)≤e2恒成立.

解(1)因为f(x)=a2lnx-x2+ax，其中x>0,所以

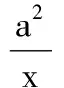
由a>0，可知f(x)的增区间为(0,a)，减区间为(a,+∞).

(2)由题意得f(1)=a-1≥e-1,即a≥e.

由第(1)小题知f(x)在[1,e]内单调递增，要使e-1≤f(x)≤e2对x∈[1,e]恒成立，只需f(x)∈[e-1,e2],即

成立，解得a=e.

点评必要与充分这样的逻辑关系可以转化成为集合的包含与被包含关系.题中恒成立问题是将充分条件转化为子集关系，再根据集合关系列出关于参数的不等式再求解即可.

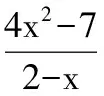
分析“任给x1∈[0,1]，f(x1)∈[-4,-3]，存在x0∈[0,1]使得g(x0)=f(x1)”，实际上，这等价于f(x)值域是g(x)值域的子集，即满足[1-2a-3a2,-2a]⊃[-4,-3],这就变成一个恒成立问题.f(x)的最小值不小于g(x)的最小值，f(x)的最大值不大于g(x)的最大值.

解对函数f(x)求导，得

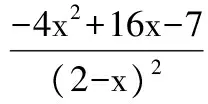
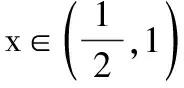
从而当x∈[0,1]时，f(x)的值域为[-4,-3].对函数g(x)求导，得

g′(x)=3(x2-a2).

因为a≥1，当x∈(0,1)时，

g′(x)<3(1-a2)≤0.

因此当x∈(0,1)时，g(x)为减函数，从而当x∈[0,1]时,有g(x)∈[g(1),g(0)].又

g(1)=1-2a-3a2,g(0)=-2a,

即当x∈[0,1]时,g(x)的值域为[1-2a-3a2,-2a],即

点评能否正确判断2个函数值域的关系是解决问题的关键，找出2个集合的包含关系，也就是找到了恒成立问题的充要条件.

2.2 利用分离变量求解

例3已知向量a=(x2，x+1)，b=(1-x，t).若函数f(x)=a·b在区间(-1，1)上是增函数，求t的取值范围.

(2005年湖北省数学高考理科试题)

分析利用导数将“函数f(x)在区间(-1，1)上是增函数”的问题转化为“f′(x)≥0在(-1，1)上恒成立”的问题，即转化成为“二次函数f′(x)=-3x2+2x+t≥0在区间(-1，1)上恒成立”，利用分离系数法将t分离出来，通过讨论最值来解出t的取值范围．

解由定义得

f(x)=x2(1-x)+t(x+1)=-x3+x2+tx+t,

从而

f′(x)=-3x2+2x+t.

若f(x)在(-1，1)上是增函数，则在(-1，1)上可设f′(x)≥0恒成立,从而f′(x)≥0,即t≥3x2-2x在(-1，1)上恒成立.考虑函数g(x)=3x2-2x的最大值为g(-1),故要使t≥3x2-2x在(-1，1)上恒成立,则t≥g(-1)，即t≥5.

而当t≥5时，f′(-1,1)在(-1，1)上满足f′(x)>0，即f(x)在(-1，1)上是增函数．故t的取值范围是t≥5.

点评在给出的不等式中，如果能通过恒等变形分离出参数,转化为函数求最值.即：若a≥f(x)恒成立，只需求出fmax(x)，满足a≥fmax(x)即可(注：若f(x)的最大值不存在，只需a≥f(x)的上界);若a≤f(x)恒成立，只需求出fmin(x)，满足a≤fmin(x)即可(注：若f(x)的最小值不存在，只需a≤f(x)的下界).

2.3 利用函数思想求解

例4已知不等式4x2-4ax+a2+2a-1≥0在区间[0,1]上恒成立，求实数a的取值范围.

分析此题分离变量比较困难，利用函数思想构造相应的函数后，就将不等式恒成立问题转化为函数值域的问题.

解根据题意构造函数

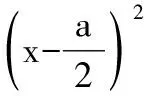
要使原不等式恒成立，fmin(x)≥0即可.

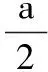
得

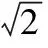
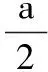
得

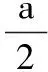
得

a>2；

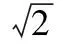
点评这类问题可以构造一个含参数的函数，根据函数性质确定参数的取值范围，主要适用于能构造出较方便求最值的函数问题.

例5求使关于x的不等式ax≥x≥logax(a>1)在区间(0,+∞)上恒成立的实数a的取值范围.

分析不等式ax≥x恒成立即使得ax-x≥0在(0,+∞)上恒成立，也就是函数f(x)=ax-x的图像在x轴及其上方，只需求fmin(x)≥0，即可求出a的范围.

解构造函数f(x)=ax-x，求导得

f′(x)=axlna-1.

同理，构造函数g(x)=logax-x，求导得

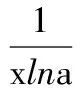
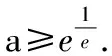
点评本题不等式的恒成立问题用函数思想构造函数，转化成函数求最值的问题.形如f(x)≥g(x)的问题，转化为h(x)=f(x)-g(x)很常见，主要看所构造的函数h(x)的最值是否容易求出.

2.4 利用变更主元求解

例6若对一切|p|≤2，不等式(log2x)2+plog2x+1>2log2x+p恒成立，求实数x的取值范围.

分析对于一切|p|≤2不等式恒成立，移项至右边为0时，不等式左边看作关于p的一次函数.

解原不等式可变形为

p(log2x-1)+(log2x)2-2log2x+1>0.

构造关于p的一次函数

f(p)=p(log2x-1)+(log2x)2-2log2x+1，

只需f(p)>0,p∈[-2,2]上恒成立即可,因此

解得

点评此类问题主要培养学生的变量意识问题．受定势思维的影响，习惯于用x来表示变量，用a,m或p等表示参数.本题中虽然指出是关于x的不等式，事实上，x和p是平等的，没有主次之分，应该是一个双变量的不等式恒成立问题．可以将p视为主元，x为参数，问题大大简化．

2.5 利用数形结合求解

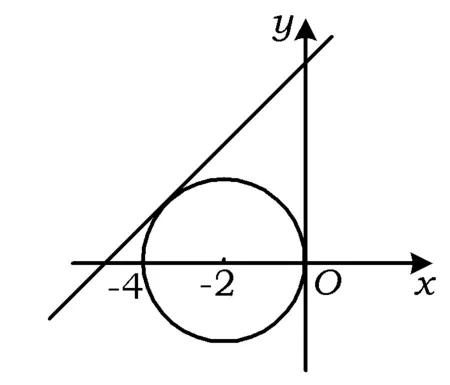
图1

(x+2)2+y2=4(y≥0),

g(x)的图像是平行的直线系

4x-3y+3-3a=0.

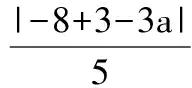
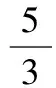
2.6 利用猜想证明求解

例8对一切实数α，不等式k(4-sinα)4+cos2α-3+k>0恒成立，求实数k的取值范围.

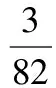
cos2α≥0，4-sinα≥3,

且

k(4-sinα)4+cos2α-3+k>k·34-3+k>

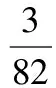
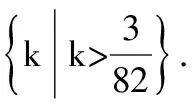
点评用前面的方法解决问题比较困难时，可以考虑由特殊到一般的思想，先考虑变量的一些特殊值，找出满足题意的参数的一部分取值，再猜想参数范围，可将问题转化为已知参数范围的情况下，证明所给的问题恒成立，来验证猜想的正确性.

3 精题集萃

4.设函数f(x)=x4+ax3+2x2+b(x∈R)，其中a,b∈R，若对于任意的a∈[-2,2]，不等式f(x)≤1在[-1,1]上恒成立，求b的取值范围．

(1)当a,b满足什么条件时,f(x)取得极值?

(2)已知a>0,且f(x)在区间(0,1]上单调递增,试用a表示出b的取值范围.

(2009年山东省数学高考文科试题)

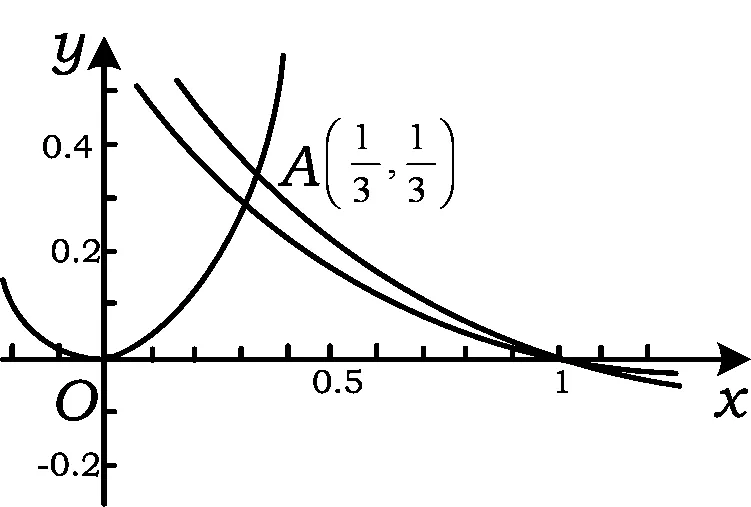
图2

参考答案

解得

综上可得

3.解设集合

A={x||x-a|

则问题可转化为A⊆B，即

亦即

4.解f′(x) =4x3+3ax2+4x=x(4x2+3ax+4).

由条件a∈[-2,2]可知

Δ=9a2-64<0，

从而4x2+3ax+4>0恒成立．当x<0时，f′(x)<0；当x>0时，f′(x)>0．因此函数f(x)在[-1,1]上的最大值是f(1)与f(-1)两者中的较大者．为使对任意a∈[-2,2]，不等式f(x)≤1在[-1,1]上恒成立，当且仅当f(x)max≤1，即

亦即

在a∈[-2,2]上恒成立,从而

解得b≤-4，因此满足条件的b的取值范围是(-∞,-4]．

5.解原不等式可化为

要使原不等式恒成立,只需

图3

此时a≤6.故满足条件的a的取值范围为(-∞,6].

6.(1)当a，b满足b2>a时，f(x)能取得极值.

从而

即