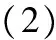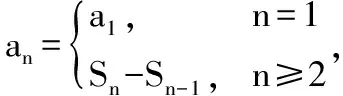数列中蕴含的“数列思想”的挖掘与运用
● (元济高级中学 浙江海盐 314300)
数列中蕴含的“数列思想”的挖掘与运用
●张艳宗卢明(元济高级中学 浙江海盐 314300)
所谓“数列思想”,是指人们在研究、解决数列问题时的思维方式以及对数列内容的本质认识.数列问题中蕴含着丰富的数列思想,在处理数列问题时,若能灵活运用这些思想,则会取得事半功倍的效果.笔者在高三数学第一轮复习教学中发现,有许多学生对数列还没有入门,缺乏主动运用数列思想来解决数列问题的意识,做题费时费力.笔者认为教学中只有重视“数列思想”的挖掘与运用,让学生站到思想的高度去认识数列的本质,才有利于学生学好数列知识.
1 通项思想
通项思想是从通项入手研究数列特性的一种思维方式.


于是,求Sn可以转化为裂项求和法来求之.
点评数列的通项是对数列中各项的统一描述,通项所具有的特性就是数列中每一项所具有的特性,这是数列的本质特征.为此,通项思想是研究数列问题的一种重要思想方法.
2 性质思想
等差数列和等比数列是2种特殊的数列,它们有许多典型的性质.对这2种数列的项的研究,既可以从定义出发,也可以从性质出发.由于性质是对数列所蕴含特性的一种本质揭示,因此,从性质出发去研究常常可以使问题更加简化.

分析由{an}是等差数列,得
a4+a12=a6+a10=2a8,
所以
a4+a6+a8+a10+a12=5a8=120,
解得
a8=24,




3 列举思想
数列是按照一定顺序排列的一列数.在研究数列问题时,把握数列的内在规律并用好规律,有利于问题的解决.有的数列问题其规律比较隐秘,不易发现,此时,扩大列举项目,有助于发现数列中隐含的规律.
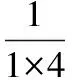
分析数列通项可拆成
从而
(1)
若只凭以上算式,很难发现消项规律.为了寻找消项规律,不妨将裂项后的项再多列举一些,并按以下形式进行排列.在式(1)中,奇数项和偶数项分别是:



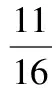
评注不少学生在求解本题时由于列举的项数不够多,导致找不到消项的规律,或找错消项的规律.可见,列举有助于发现规律,在数列学习过程中自觉养成“列举”的意识非常重要.需要指出的是通过列举揭示规律,运用到的逻辑是不完全归纳法,因此,列举数量的多少会影响猜想的正确性.
4 补白思想
“补白”是指在求解数列问题时,通过适当补上一些项,使得表达式的意义更加完整,有利于发现规律,达到问题简化之目的.
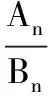
分析条件给出的是数列的和的比值,要求的是数列项的比值,如何进行和与项的转换呢?
我们知道,在等差数列{an}中,a6前面有5项,如果在a6后面再补上5项,使a6处在正中间的位置,由等差数列的性质知
A11=a1+…+a5+a6+a7+…+a11=11a6,
同理
B11=11b6,
故
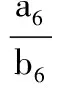

5 还原思想


评注当然,若将通项按奇数项、偶数项写成分段函数的形式,可以不作“还原”处理,但这样的通项不漂亮.数列题目在编题时为了考查学生思维的灵活性,常常会通过一些特殊处理来隐匿规律,而“还原法”则能让隐匿的规律显现出来.
6 子数列思想
从原数列项中取出一些项构成一个新的数列,称此新数列是原数列的子数列.所谓“子数列思想”,就是能够自觉地意识到子数列的项具有“双重身份”,它们既是原数列的项,又是子数列的项.这是解决子数列问题的关键.
例6已知数列{an}是等差数列(d≠0),从数列{an}中抽取部分项ak1,ak2,…,akn成等比数列,且k1=1,k2=5,k3=17,求数列{kn}的通项.
分析ak1,ak2,…,akn这个数列有双重身份:是原数列(也称母数列){an}中的项,{an}是等差数列;又是子数列{akn}中的项,{akn}是等比数列.
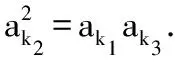
(a1+4d)2=a1(a1+16d),
解得
a1=2d,
即
ak1=2d,ak2=6d,ak3=18d,
于是

从而子数列{akn}的通项是
akn=ak1qn-1=2d·3n-1.
又在母数列{an}中,
akn=a1+(kn-1)d=(kn+1)d,
从而
(kn+1)d=2d·3n-1,
解得
kn=2·3n-1-1.
评注由于子数列的每一项都拥有“双重身份”,因而它们同时满足原数列的相关条件,又满足子数列的相关条件,如可以分别用原数列和子数列的通项公式来表示子数列的项等.解子数列问题时,学生思维受阻的原因是未能用好子数列项的“双重身份”,即缺乏“子数列思想”.
7 函数思想
从映射的角度看,数列本质上是一个定义在正整数集的子集上的函数.因此,用函数的观点理解数列,用研究函数的相关方法来研究数列,是解决数列问题的有效方法.
例7在等差数列{an}中,已知a1=15,S4=S12,当n为何值时Sn有最大值?
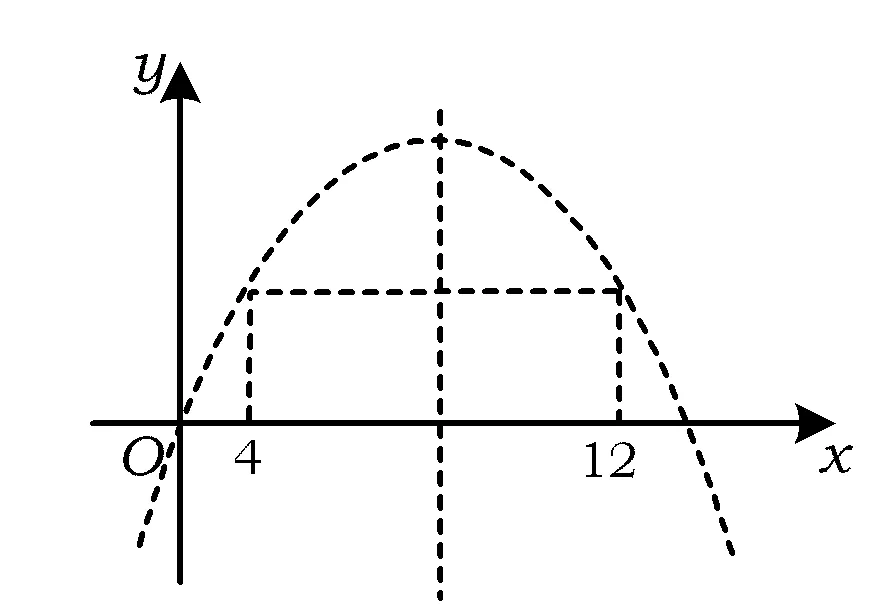
图1
分析为什么这个等差数列的前n项和Sn有最大项?其首项a1=15>0,故它的前几项为正,从某项起开始变号.常规的做法是通过找到变号的项来求解,这是纯数列解法.等差数列前n项和Sn是关于n的二次型函数,该函数解析式的常数项为0,其图像是过原点的抛物线上横坐标为正整数的点(为便于分析,将这些散点用虚线连接,如图1所示).由题意可知该数列公差d<0,抛物线图像开口向下,S4=S12说明此抛物线有对称轴n=8,故当n=8时,Sn最大.
评注把数列看作一种特殊的函数,利用函数思想,通过数形结合来求解,既直观又简洁.如果将此题进行变式,将条件中的“S4=S12”改成“S4=S11”,其他不变.用“函数思想”求解,其优越性会更加凸显.
8 整体思想
整体思想就是从整体着眼,通过对问题的整体形式、整体结构进行处理,以达到简化求解过程之目的.
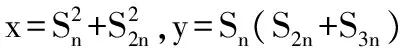
( )
A.x>yB.x=y
C.x 分析由Sn=a1+a2+…+an, S2n=a1+…+an+an+1+…+a2n= Sn+qnSn=Sn(1+qn), S3n=Sn(1+qn+q2n), Sn(Sn-S3n)+S2n(S2n-Sn)= Sn(1+qn)·Snqn-Sn·Sn(q2n+qn)=0. 评注将a1+a2+…+an,an+1+an+1+…+a2n,a2n+1+a2n+2…+a3n分别看成一个整体,从而建立S2n,S3n与Sn的关系,简化计算. 所谓递推思想,就是利用给定的递推关系逐步递推,直到得出期望的结果的思维方法. 例9平面内有n个圆,其中每2个圆都相交于2个点,且每3个圆都不相交于同一点,则n个圆把平面分成______个区域. 分析记n个圆将平面平分f(n)个部分,n个圆中的n-1个圆将平面分成f(n-1)个部分,第n个圆被前n-1个圆分成2(n-1)条弧,每条弧把它所在的区域分成2块,增加了2(n-1)个部分,即 f(n)-f(n-1)=2(n-1). 根据这一递推关系得到 f(n-1)-f(n-2)=2(n-2), f(n-2)-f(n-3)=2(n-3), … f(2)-f(1)=2. 而f(1)=2,累加得到 f(n)=n2-n+2. 评注在求解n个圆把平面分成多少个区域时,先分清n-1个圆到n个圆将平面划分区域的变化规律,建立起f(n)与f(n-1)之间的递推关系,从而解决问题. 假设数列{an}的通项an=f(n),则函数h(n)=f(n+1)-f(n)称为函数f(n)的一阶差分,r(n)=h(n+1)-h(n)为函数f(n)的二阶差分.如等差数列{an}的通项an是前n项和Sn的一阶差分,公差是通项an的一阶差分,是前n项和Sn的二阶差分.差分是微分的离散形式,是研究数列{an}与前n项和Sn有关问题的重要方法. 例10设数列{an}的前n项和为Sn,已知a1=1,a2=6,a3=11,且满足(5n-8)Sn+1-(5n+2)Sn=An+B(n=1,2,3…),其中A,B是常数. (1)求A与B的值; (2)证明:数列{an}为等差数列. 分析(1)令n=1,则 令n=2,则 式(2)-式(3),得 A= 2(S3-S2)-7(S2-S1)= 2a3-7a2=-20, 从而 B= -3S2-7S1-A= -3×7-7×1+20=-8. (2)由第(1)小题知 (5n-8)Sn+1-(5n+2)Sn=-20n-8. (4) 当n≥2时, [5(n-1)-8]Sn- [5(n-1)+2]Sn-1= -20(n-1)-8. (5) 式(4)-式(5),并整理得 (5n-8)(Sn+1-Sn)-(5n-3)(Sn-Sn-1)=-20, 即 (5n-8)an+1-(5n-3)an=-20(n≥2). (6) 当n≥3时, 式(6)-式(7),并整理得 (5n-8)(an+1-an)=(5n-8)(an-an-1), 从而 an+1-an=an-an-1(n≥3). 又a3-a2=11-6=5,a2-a1=6-1=5,于是 an+1-an=an-an-1=5(n≥2), 即{an}是公差为5的等差数列. 总之,特定的数学内容,如函数、三角、数列、概率等,都有其特有的研究方法和手段.虽然有的方法可以互通,但更多的是个性化的思维和研究手段.只有掌握了这种个性化的技能,才算是对这块内容学习的“入门”.前面提及的“数列思想”就是研究数列问题的一种个性化的技能,它是学习数列的“灵魂”.它不是完全抽象、空洞的技能,而是以数列知识为载体,是客观存在的内容,是对数列知识和解决问题策略的一种概括和提炼,具有应用性和指导性.实践证明,重视“数列思想”的挖掘与运用,是帮助学生数列“入门”的重要环节. [1] 徐章韬.差分思想在数列中的应用[J].数学教学,2012(2):22-23.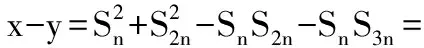
9 递推思想
10 差分思想