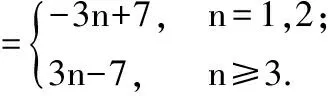灵活多变的数列综合题
● (武岭中学 浙江奉化 315502)
灵活多变的数列综合题
●杨亢尔(武岭中学 浙江奉化 315502)
1 考点回顾
数列作为高中数学学科知识的主干内容,历来是高考重点考查的内容之一.高考关于数列的命题大致可分为2种类型:(1)考查数列本身的有关知识,如等差数列与等比数列的概念、性质、通项公式和数列的求和公式、递推关系等;(2)考查数列与其他知识结合的问题,如数列与函数、方程、不等式、几何等的结合及数列的实际应用等.纵观近3年的浙江省数学高考数列题,无论是文科还是理科,尽管题型和分值屡有变化,但从数列基础知识入手,注重对数列知识的理解和应用,注重对数学思想、方法和能力灵活多变的考查没有变,这也充分体现了数学高考“以能力立意”的指导思想.
值得一提的是,与其他省市数学高考数列试题相比,浙江省的数列试题无论是难度还是综合性都显得更为平和、适中而易于把握,这应该与浙江省数学自主命题不特别强调在知识网络交汇处设计试题的考试要求有关.相信在深化普通高中课程改革的新形势下,浙江省教育考试院还将继续深化高考命题改革,切实控制试题难度,重视教材和基础知识、基本方法、基本技能,“常规试题作考题,平淡之中见功底”,为高中数学教学发挥更好的导向作用.
2 典例剖析
例1 已知等差数列{an}和等比数列{bn}满足a1=b1=1,a2=b3=4,这2个数列的公共项按原顺序组成数列{cn}.
(1)求数列{an},{bn}的通项公式;
(2)判断数列{cn}是等差数列还是等比数列?试证明你的结论.
分析容易求得数列{an},{bn}的通项公式分别为an=3n-2,bn=2n-1.这2个数列的公共项的前3项依次为1,4,16,猜想{cn}是公比为4的等比数列,可用如下方法加以验证:
若cn是数列{an},{bn}的一个公共项,不妨设cn=am=bk(n,m,k∈N*),于是cn=3m-2=2k-1,下面考察它们的后续项中公共项的情况:
因为
bk+1= 2k=2·2k-1=6m-4=3(2m-1)-1,
所以
bk+1∉{an}.
又
bk+2=2k+1=4·2k-1=12m-8=3(4m-2)-2,
从而
bk+2∈{an},
故这一项就是数列{cn}的第n+1项,即
cn+1=bk+2=2k+1,
且

这就证明了{cn}是公比为4的等比数列,其通项公式为cn=4n-1.
也可以这样来考虑:根据{cn}的前3项1,4,16,…,猜想cn=4n-1.由于4n-1=2(2n-1)-1,故cn=4n-1必是数列{bn}中的项,因此只需证明它也是{an}中的项即可.由于
这就证明了cn=4n-1也是{an}中的项,从而可知{cn}是公比为4的等比数列.
评注本题主要考查等差和等比数列的定义、通项公式等基础知识,入手容易,设问新颖,无论是整数性质的变形,二项展开式的应用,还是合情推理的证明,都围绕数列通项公式展开,较好地体现了以知识为载体、以方法为依托、以能力为考查目的的命题指向.
例2 已知数列{an}的前n项和为Sn,且a2an=S2+Sn对一切正整数n都成立.
(1)求a1,a2的值;
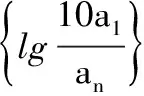
(2012年四川省数学高考试题)
分析在a2an=S2+Sn中分别令n=1,2,即可求得a1,a2的值,再利用数列的前n项和Sn与数列的通项an的关系
不难将an与Sn的递推关系转化为an与an-1的关系式
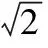
因此
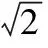



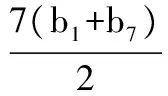
评注本题主要考查等差数列、等比数列、对数等基础知识,以及函数与方程、分类与整合、化归与转化等数学思想,同时考查思维、运算、分析问题和解决问题的能力.本题涉及等差数列前n项之和的最值问题,既可以通过分析项的正负来确定,也可以先求和再利用二次函数的性质加以解决,要快速、准确、无误地完成解答,既要求通性通法与巧妙方法双管齐下,更需要有扎实的数学功底.
例3 函数f(x)=x2-2x-3,定义数列{xn}如下:x1=2,xn+1是过点P(4,5),Qn(xn,f(xn))的直线PQn与x轴交点的横坐标.
(1)求xn+1关于xn的递推关系式;
(2)证明:2≤xn (2012年全国卷数学高考试题改编) 分析由于点P(4,5)在函数f(x)的图像上,故过所给出的点P(4,5),Qn(xn,f(xn))的直线PQn的斜率一定存在,通过直线与坐标轴的交点可得到数列的递推公式.直线PQn的直线方程为 在第(2)小题中,一方面,2≤xn<3可用数学归纳法加以证明: 当n=1时,x1=2,满足2≤x1<3,假设n=k时,2≤xk<3成立,则当n=k+1时, 由2≤xk<3,得 4≤xk+2<5, 即 从而 亦即2≤xk+1<3也成立. 综上可知,2≤xn<3对任意正整数恒成立. 另一方面,xn 又2≤xn<3,得 1≤xn-1<2, 即 0<-(xn-1)2+4≤3, 故 xn+1-xn>0, 从而 xn 综上可知,2≤xn 评注本题以函数为背景,考查了直线方程、函数解析式、数列的递推公式以及不等式证明中的取差比较法和数学归纳法等,综合性较强,特别是对代数式的变形和运算有较高的要求.做这类试题需根据已知条件,一步一步地转化为代数式,再化简得到要找的关系式. 本例中xn+1关于xn的分式线性递推关系是一种常见的递推数列,有兴趣的读者不妨尝试用多种方法求出数列{xn}的通项公式. 例4 设数列{an}的前n项和为Sn,满足2Sn=an+1-2n+1+1(n∈N*),且a1,a2+5,a3成等差数列. (1)求a1的值; (2)求数列{an}的通项公式; (2012年广东省数学高考试题) 分析本题以数列的通项与前n项和的关系式给出,此类问题的一般解法是将其转化成仅含有通项或仅含有前n项和的关系式,再化归成等差或等比数列来处理. (1)由2Sn=an+1-2n+1+1可得 2Sn+1=an+2-2n+2+1, 两式相减得 an+2=3an+1+2n+1, 于是 a3=3a2+4. 又 2a1=a2-3,a1+a3=2(a2+5), 可得 a1=1,a2=5. (2)显然an+1=3an+2n对任意n∈N*均成立,要求数列{an}的通项公式,有如下多种方法: 方法1(参数法)不妨设 an+1+λ·2n+1=3(an+λ·2n), 则 an+1=3an+λ·2n, 得 λ=1, 故{an+2n}是首项为3,公比为3的等比数列,因此 an+2n=3n, 即 an=3n-2n. 方法2(化归为一阶线性递推数列)由 an+1=3an+2n, 两边同除以2n+1得 从而 于是 an=3n-2n. 方法3(累加法)由 an+1=3an+2n, 两边同除以3n+1得 累加可得 从而 an=3n-2n. 3n>2×2n, 从而 an>2n, 即 于是 也可利用2·3n-1=2·(2+1)n-1>2n,得 3n-2n>3n-1(n≥2), 评注本题主要考查了数列的通项公式、求和、递推数列、不等式的证明等知识,思想方法涉及函数与方程、归纳与转化、特殊与一般、分类讨论等,属于较难题,旨在考查学生分析、归纳、探究和推理论证问题的能力.其中第(2)小题求形如an+1=k·an+an递推数列通项时用到的3种方法,对于求简单递推数列通项公式具有非常现实的借鉴意义,值得细细品味. 1.已知等差数列{an}前3项的和为-3,前3项的积为8. (1)求等差数列{an}的通项公式; (2)若a2,a3,a1成等比数列,求数列{|an|}的前n项和. (2012年湖北省数学高考试题) (1)确定常数k,求an; (2012年江西省数学高考试题) (1)求数列{an}的通项公式及Sn; (2011年浙江省数学高考试题) 4.设{an}是公比不为1的等比数列,其前n项和为Sn,且a5,a3,a4成等差数列. (1)求数列{an}的公比; (2)证明:对任意k∈N*,Sk+2,Sk,Sk+1成等差数列. (2012年陕西省数学高考试题) 5.在等差数列{an}中,a3+a4+a5=84,a9=73. (1)求数列{an}的通项公式; (2)对任意m∈N*,将数列{an}中落入区间(9m,92m)内的项的个数记为{bn},求数列{bn}的前m项和Sm. (2012年江西省数学高考试题) 6.已知数列{an}和{bn}的通项公式分别为an=3n+6,bn=2n+7(n∈N*),将集合{x|x=an,x∈N*}∪{x|x=bn,n∈N*}中的元素从小到大依次排列,构成数列{cn}. (1)求c1,c2,c3,c4; (2)求证:在数列{cn}中,但不在数列{bn}中的项恰为a2,a4,…,a2n,…; (3)求数列{cn}的通项公式. (2011年上海市数学高考试题) 参考答案 1.(1)an=-3n+5或an=3n-7; 4.(1)q=-2. (2)证法1因为 Sk+2+Sk+1-2Sk= (Sk+2-Sk)+(Sk+1-Sk)= ak+1+ak+2+ak+1= 2ak+1+ak+1·(-2)=0, 所以,对任意k∈N*,Sk+2,Sk,Sk+1成等差数列. 因此,对任意k∈N*,Sk+2,Sk,Sk+1成等差数列. 5.(1)an=9n-8; (2)提示:对m∈N*,若9m 9m+8<9n<92m+8, 从而 9m-1+1≤n≤92m-1, 因此 bm=92m-1-9m-1, 可得Sm= (9+93+…+92m-1)-(1+9+…+9m-1)= 6.(1)c1=9,c2=11,c3=12,c4=13; (2)提示:对任意n∈N*,有 a2n-1=6n+3=2(3n-2)+7∈{bn}, a2n=6n+6∉{bn};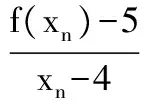

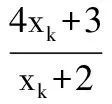
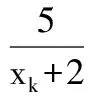
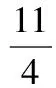

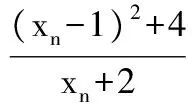


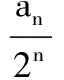
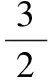


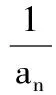
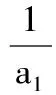
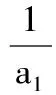

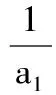
3 精题集萃