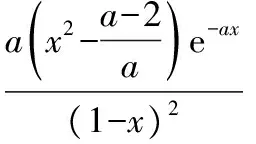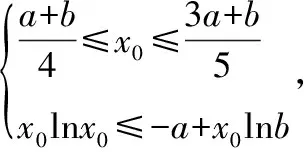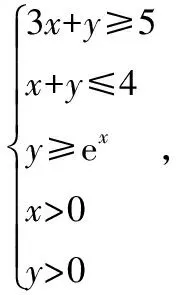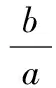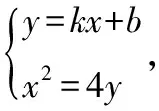导数及其应用
● (黄岩中学 浙江黄岩 318020)
导数及其应用
●金克勤(黄岩中学 浙江黄岩 318020)
导数及其应用是数学高考的重点,特别在理科数学考试中往往承担压轴的大戏.由于导数具有丰富的数学内涵和表现形式,与函数的图像、性质以及方程、不等式之间的紧密联系,故成为高考命题青睐的对象.
1 考点回顾
高考数学的导数及其应用,主要考查:
(1)导数的概念及其几何意义.特别是函数在某一点的导数为其图像上经过该点的切线的斜率.在试题中往往以求切线方程的形式出现.
(2)导数与函数性质的关系.特别是导函数的符号与函数单调性的关系、极值与最值的关系、函数的值域与参数的范围等.在试题中往往以求函数的单调区间、证明函数的单调性、求函数的最值或值域等形式出现.
(3)导数与方程、不等式的关系.特别是讨论方程解的个数、求与函数相关的不等式的解集、讨论参数的范围、利用函数单调性证明不等式等.
(4)导数与函数图像的关系.特别是对函数图像形状的判断、极值点的位置、函数图像的变化规律、函数图像与直线等其他图形的位置关系等.
(5)值得关注的是近几年高考中,导数及其应用的考查出现了新的变化,主要集中在解析几何中的面积、距离等几何量最值问题的计算,以及在非线性不等式组所确定的可行域内求目标函数最值问题,都开始利用导数进行计算.
因此,在导数及其应用的复习过程中,应充分体现以下几个重点:首先是导数的基本概念及其几何意义,这是学习导数与运用导数解决问题的基础;其次是掌握导数的运算及其运算法则,以及简单复合函数的导数计算,这是运用导数解决问题的工具;第三,要理解利用导数解决与函数有关的问题时,函数单调性的讨论处于核心的地位,要将所研究的问题转化成为关于单调性问题的讨论,这是运用导数解决问题的关键.
要重视对一些常见函数和常考函数的研究.纵观近几年高考试题中导数及其应用部分所涉及到的函数主要有以下几种类型:


2 典例剖析
2.1 函数的极值与单调性
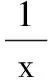
分析函数f(x)的定义域为(0,+∞),且
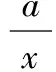
(1)当a≤0时,f′(x)≤0,因此f(x)在定义域(0,+∞)上单调递减;

评注求函数单调区间的本质是判定其导函数f′(x)的符号,先求出函数的导函数,再判断导函数的符号.在判断导函数的符号时,可利用不等式的性质、函数单调性等,有时可运用分类讨论的思想来进行符号的判定.
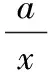
分析函数f(x)的定义域是(0,+∞),因为函数f(x)存在极大值和极小值,且
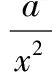
所以
4-4a2>0,
即

设方程ax2-2x+a=0的2个根为x1,x2,且x1 m=f(x1),n=f(x2). 将S表示成关于参数a的函数,实际上将问题转化成了求函数值域的问题. 因此S(t)是关于t的增函数,从而 即 评注求函数极值问题,其本质是在一定的范围内求方程的解,以及求函数值的问题.对于方程根的存在性以及方程根的分布讨论已成为高考中的热点问题之一,因此掌握好与方程相关的知识,了解函数与方程间的关系是提高解题能力的重要环节. 2.2 函数的最值与参数的范围 例3已知函数f(x)=ax+lnx,其中a∈R. (1)当a=-1时,求函数f(x)的最大值; (2)若f(x)在区间(0,e]上的最大值为-3,求a的值; 评注在闭区间上,一个连续函数必定存在最大值和最小值,函数的最值只能在区间端点或极值点取到.在开区间上,如果函数有唯一的极大值点(极小值点),那么这个极大值(极小值)便是函数在这个区间上的最大值(最小值),这是一个常用的原理. ①当a≥0时,f′(x)>0,函数f(x)在区间(0,e]上是增函数,fmax(x)=f(e)=ae+1=-3,矛盾. fmax(x)=f(e)=ae+1=-3, 得 得a=-e-2. 评注在定义域内的一个子区间上求函数的最值,极值点的位置很重要.如果极值点又与参数有关,那么就需要对参数进行分类讨论以确定极值点的位置.这种类型的问题也是高考的热点问题之一. 评注讨论方程有无实数解,或有多少实数解,一般的方法是转化成分析函数图像的交点问题.我们可以先考虑函数的最值,确定大致的位置关系,估计函数图像有无交点的可能,要避免未加分析马上进行复杂函数的求导运算. 例4已知a>0,b∈R,函数f(x)=4ax3-2bx-a+b.证明:当0≤x≤1时, (1)函数f(x)的最大值为|2a-b|+a; (2)f(x)+|2a-b|+a≥0. fmax(x)=max{f(1),f(0)}. 因为f(1)=3a-b,f(0)=b-a,f(1)-f(0)=4a-2b,所以 即 得 fmax(x)=|2a-b|+a. 评注求闭区间上函数的最值问题始终应该关注函数单调性这个关键因素. (2)要证明f(x)+|2a-b|+a≥0,即证明f(x)+fmax(x)≥0,亦即证明当2a-b≥0时,f(x)+f(1)≥0;当2a-b≤0时,f(x)+f(0)≥0. ①当2a-b≥0时, f(x)+f(1)= 4ax3-2bx+2a≥4ax3-4ax+2a= 2a(2x3-2x+1), ②当2a-b≤0时, f(x)+f(0)= 4ax3-2b(1-x)-2a≥ 2a(2x3-2x+1), 于是问题转化成为证明函数φ(x)=2x3-2x+1,当x∈[0,1]时,φ(x)≥0. 评注函数的最值是函数的整体性质,因此需要对函数在某范围内的变化规律有充分的了解,这样更容易寻找到正确的解题方法. 2.3 导数与函数不等式 分析由于 f(x1)-f(x2) 即 f(x1)+x1 因此结论是成立的. 由题意,必须有f(1)=1-2a≤-1,即a≥1,而当a≥1时,x=1是函数f(x)唯一的极大值点,因此 fmax(x)=f(1)=1-2a≤-1, 故a的取值范围是[1,+∞). 当且仅当x=1时等号成立,因此gmax(x)=1,即a≥1.这种处理问题的思路在2012年的数学高考中也有体现,如山东卷理科第22题 要证明g(x)<1+e-2,当x≥1时,显然有g(x)≤0,而当0≤x≤1时,如果直接求函数g(x)的最大值,那么因为求导数的运算非常复杂而使解题过程无法继续.我们同样可以利用不等式ln(1+x)≤x的变形,得到g(x)≤1-xlnx-x,只要证明当0≤x≤1时,函数y=1-xlnx-x≤1+e2即可. 另外,在求参数范围的过程中,也可以利用特殊值,缩小参数的范围,简化问题的讨论. 2.4 导数与函数的图像 例7已知函数f(x)=eax-x,其中a≠0.在函数f(x)的图像上取定2个点A(x1,f(x1)),B(x2,f(x2))(x1 f′(x)=aeax-1. 评注导数问题往往都具有很强的几何背景,本题的几何背景是微分中值定理在一个具体函数上的表现.割线AB的斜率介于过点A,B的曲线的切线的斜率之间,并且存在一点x*,使f′(x*)=kAB,而且f′(x)是增函数. (1)证明:对于正数a,存在正数p,使得当x∈[0,p]时,有-1≤f(x)≤1; (2)设(1)中的p的最大值为g(a),求g(a)的最大值. 分析因f(0)=1,且 f′(x)=3x2+3(1-a)x-3a=3(x+1)(x-a), 因此,x=-1是函数f(x)的极大值点,x=a是函数f(x)的极小值点,从而f(x)是(0,a)上的减函数.从函数f(x)的图像上看,问题(1)中的结论是非常明显的,正数p显然是存在的,但如何说明? 当f(a)≥-1时,可取p=a,此时当x∈[0,p]时,有-1≤f(x)≤1成立;而当f(a)<-1时,由于f(0)+1=2>0,f(a)+1<0,因此存在一个数p∈(0,a),使f(p)+1=0,此时当x∈[0,p]时,有-1≤f(x)≤1成立. 评注导数应用的一个重要方面是对于函数图像的分析和讨论,这是体现数形结合思想的重要标志,这也是高考的热点之一.本题中 由此知道函数f(x)的图像经过2个定点(0,1),(-2,-1),经过这2个定点的直线方程为y=x-1,于是我们可以将函数f(x)改写成 f(x)=(x+1)+x(x+2)(x-x0), 因此 导数及其应用问题虽然较为综合,也有一定的难度,但是它所体现的数学价值是其他内容所不能替代的,因而无可厚非地成为高考的热点.只要我们真正领会其中的数学内涵,就能很好地把握问题的本质,从而正确地解决问题. 1.设函数f(x)=xex,则 ( ) A.x=1为f(x)的极大值点 B.x=1为f(x)的极小值点 C.x=-1为f(x)的极大值点 D.x=-1为f(x)的极小值点 ( ) 3.函数f(x)=x3-4x+a,0 ( ) A.x1>-1 B.x2<0 C.x2>0 D.x3>2 5.定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离.已知曲线C1:y=x2+a到直线l:y=x的距离等于曲线C2:x2+(y+4)2=2到直线l:y=x的距离,则实数a=______. (1)设a>0,讨论函数y=f(x)的单调性; (2)若对任意x∈(0,1),恒有f(x)>1,求实数a的取值范围. 7.设a>0,b>0,函数f(x)=xlnx,g(x)=-a+xlnb. (1)设h(x)=f(x)-g(x),求函数h(x)的单调区间; 8.已知抛物线C:x2=4y,抛物线上点A,B分别位于y轴的两侧,直线l经过抛物线的焦点且平行于x轴.过点A,B分别作抛物线的切线l1,l2,l1与l2相交于点P,且与直线l分别相交于点M,N,求△PMN面积的最小值,并求取到最小值时点A,B的坐标. 参考答案 (2)a的取值范围是(-∞,2]. (2)解法1分类讨论: 则 8.提示:设A(x1,y1),B(x2,y2),其中x1<0,x2>0.由 得 由 得 同理可得 因此 x2-4kx-4b=0, 从而 x1+x2=4k,x1x2=-4b, 于是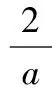

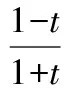



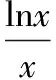
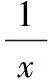
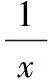

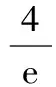

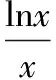
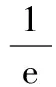

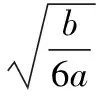
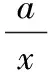
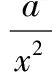

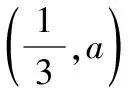
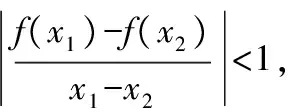

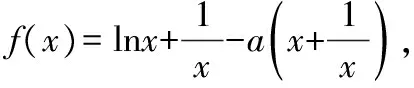


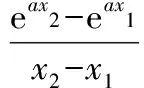
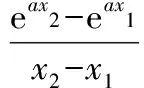

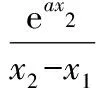
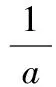


3 精题集萃