高三数学复习如何做到“正本清源”
● (嘉兴市第一中学 浙江嘉兴 314050)
高三数学复习如何做到“正本清源”
●陈云彪(嘉兴市第一中学 浙江嘉兴 314050)
每年进行高三复习时,总有些学生的解题能力没有达到教师所想要的理想的程度.每次测验下来,学生的有些错误出乎意料,认真分析原因,主要在于学生对数学概念的理解不到位.因为对概念理解不够透彻,所以在基本方法的使用上不够灵活、熟练,一旦碰到新的题目,就会没有思路.因此,教师在教学中要加强数学思想和数学概念的教学.
下面笔者结合自己在平时教学中的一些体会,来谈谈解决此类问题的具体方法.
1 控制教学中的难度,强化数学基本概念的教学
平时的教学难度太大往往会弱化教师对概念教学的深化,究其原因是多方面的,但主要是教师在复习认识上的问题.教师普遍的观点是:会当凌绝顶,一览众山小;喜欢难,不强调基础.笔者认为这样做有许多弊端:其一,会使许多学生在高一、高二时学得不理想,在高三时得不到很好地加强;其二,教师任意地拔高难度,从而使一部分学生逐渐失去学习数学的信心;其三,养成了学生“好高骛远、不踏实做题”的习惯.这样,我们的复习就无法达到预期的效果.
譬如在复习“直线和圆的位置关系”时,笔者安排的第1个例题如下:
例1求过原点且倾斜角为60°的直线被圆x2+y2-4y=0所截得的弦长.
这个例题非常简单,涉及到直线和圆位置关系的基本处理方法,主题非常明确.
方法1(解析几何法)
解析几何处理问题的核心方法是2个方程联立.

得到交点坐标,再利用两点之间的距离公式求解.
评注方法1体现了解析几何处理问题的基本方法:用代数运算来处理几何问题.它是整个解析几何教学的核心,在平时的教学中要强化.很多教师认为这对于解决与圆有关的问题未必是好的方法,因此在平时教学中未给予重视.这样的处理是不足取的,久而久之,会弱化学生对解析几何本质的认识.
方法2(利用圆的性质)
在初中阶段,学生已学过许多圆的性质,这些性质往往有助于简化问题的解决.

x2+(y-2)2=4,

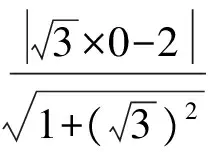
因此直线被圆截得的弦长为
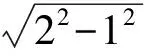
评注方法2和方法1相比,简化了计算.学生认识到处理解析几何问题的特点:用代数法来处理几何,使许多的几何问题得到了很好的解决.但在解决问题时,若能适当地运用一些几何性质,往往会使问题得到简化.
例1的设计非常巧妙,在平时解决解析几何题目时重视图形作用的学生,得到如下更为简捷的方法:

图1

一个简单的题目,通过3种基本方法的对比,使学生对解析几何中有关圆问题的解题策略有了较深刻的理解,相信他们在以后的解题过程中会找到合适的方法.
2 重视对经典题目的剖析,切忌过分追求“新”、“奇”
高三复习的资料更新十分及时,但有些资料由于编者时间上的仓促,往往选题上没有斟酌,因此无论题目还是解题过程,没有很好地体现一个“例”字.教师在强调题目“新”的同时,往往忽视了一些经典题目在教学中所起的作用.笔者认为经典题目之所以经典,首先在于题目本身包含了重要的解题思想,再者对学生而言,它未必就是陈题.教师还是要强调其在教学中的价值,要在教学上花功夫,推陈出新,使经典题目展示新的含义.下面来看一个直线和圆问题中的经典题目:
例2已知圆x2+y2+x-6y+m=0与直线x+2y-3=0相交于点P,Q,O为原点,且OP⊥OQ,求实数m的值.
对于这个问题,通常的解法是:
方法1联立方程
得
5y2-20y+12+m=0,
因此
(1)
由OP⊥OQ,得
x1x2+y1y2=0,
从而
9-6(y1+y2)+5y1y2=0,
将式(1)代入,得

解得
m=3.
除了常规方法,经过思考,例2还可以用以下2种方法解决.
方法2(利用平面几何)
当OP⊥OQ时,点P,Q,O共圆(不妨设此圆的圆心为M),且圆M的直径就是PQ.设圆x2+y2+x-6y+m=0的圆心为N,圆心N和PQ中点的连线与已知直线x+2y-3=0垂直,其方程为

图2
即
2x-y+2=0.
联立

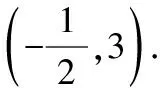
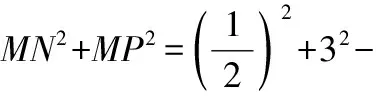
而在圆M中,因为PQ是直径,所以
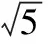
解得
m=3.
评注比较方法1与方法2,发现在有关直线和圆位置关系的题目中,常规的解题方法还是具备普遍意义的.因此在平时的教学中要强调数学的同性同法,真正的“清本正源”,对方法发生、发展过程要清楚地分析,这样有助于学生对知识的理解,学生的解题能力也会有很大的提高.
方法3(利用圆系方程)
当OP⊥OQ时,点P,Q,O共圆(不妨设此圆的圆心为M),且此圆的直径就是PQ,即PQ的中点即为圆心M.设圆x2+y2+x-6y+m=0的圆心为N,圆心N和PQ中点的连线与已知直线x+2y-3=0垂直,其方程为
即
2x-y+2=0.
联立
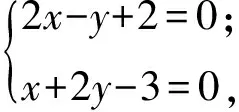
得点M的坐标为(-1,2).由此可设圆M为
(x+1)2+(y-2)2=r2.
因为此圆过原点,所以
(x+1)2+(y-2)2=r2,
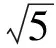
(x+1)2+(y-2)2=5.
而圆M和圆N的公共弦为
(x+1)2+(y-2)2-5-(x2+y2+x-6y+m)=0,
即
x+2y-m=0.
此方程就是
x+2y-3=0,
故
m=3.
3 防止脱离课本,天马行空
高三复习时所选用的资料是非常完备的,几乎是教师怎么想,资料就怎么做,但正因为这样,也养成了教师对复习资料的依赖性.笔者认为资料和课堂教学一样,要想真正成为自己的东西,还是需要好好地整合.在复习过程中,不要脱离课本,天马行空式地复习,这样做不仅效率低,而且学生对数学概念的理解依旧不会出现好转.因此,想要把教师和学生从题海战术中解脱出来,关键在于重视教材的应用.下面来看这样一个问题:
例3一个口袋内有带有标号的大小相同的7个白球和3个黑球,现从中摸出2个球,求一黑一白的概率.
学生给出了2种不同的解法:
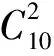
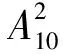
评注在这个问题中,学生有3个困惑之处:
(1)球是不是有区别?
(2)摸出的球是否要排序?
(3)为什么2种方法得到的结论一样?
其实例3可以利用《数学(必修3)》第127页的例题——给球贴标签的方法来处理.本来球是不是有区别,我们不去管它,现在对球进行贴标签来加以区别,然后再利用古典概型的基本概念加以解决.如果球贴了标签,那么球与球之间就有所区别了,方法2就较容易理解了.
解决问题之后把标签擦掉,请思考:在摸出球之后,附加一个“把球上的标签擦掉”的动作,会改变事件的概率吗?这显然是不合情理的.
这里笔者只是举例说明,在教材中许多地方都有这样的数学思想,在平时的复习中要好好利用.数学复习的重点不仅仅指熟悉其知识点,更重要的是掌握其提供的方法.

