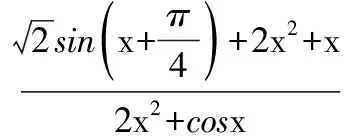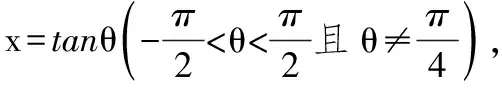函数中的“两域四性”
● (龙湾中学 浙江温州 325024)
函数中的“两域四性”
●刘建永徐登群(龙湾中学 浙江温州 325024)
1 考查要求
会求一些简单的函数定义域和值域;理解函数的单调性,会讨论和证明函数的单调性,理解函数的奇偶性,会判断函数的奇偶性;了解三角函数的周期性;会运用函数图像理解和讨论函数的性质.
2 考点回顾
函数在高中数学中的地位毋庸置疑,高考对于函数的考查是多方位的,但考查的基石却是明确的,即函数的“两域四性”:定义域、值域;单调性、奇偶性、周期性、对称性.近几年高考关于“两域四性”的考查主要表现在:
(1)与函数“两域四性”有关的选择题、填空题,这类题型主要考查函数“两域四性”的基础知识;
(2)与函数的图像相结合,运用数形结合、函数与方程等数学思想解决有关函数“四性”的问题;
(3)与解析几何、导数、方程、不等式等知识交汇在一起,解决有关恒成立、最值等问题.
3 典例剖析
类型1回归基础,求函数的定义域
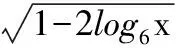
(2012年江苏省数学高考试题)

评注本题的突破口是为寻找使函数解析式有意义的限制条件.

分析f(x)的定义域是[-1,2],意思是凡被f作用的对象都在[-1,2]中,由此可得
从而
即
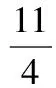

评析这类问题的一般形式是:已知函数f(x)的定义域是A,求函数f(φ(x))的定义域.正确理解函数符号及其定义域的含义是求解此类问题的关键.这类问题实质上相当于已知φ(x)的值域A,据此求x的取值范围.
类型2转换角度,求函数的值域
例3已知t为常数,函数y=|x2-2x-t|在区间[0,3]上的最大值为2,则t=______.
(2008年浙江省数学高考理科试题)
分析由于x∈[0,3],从而
x2-2x=(x-1)2-1∈[-1,3].
又因为函数y=|x2-2x-t|的最大值为2,所以t=1.
评注本题主要考查二次函数和绝对值函数的值域问题,可从绝对值的几何意义考虑.
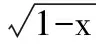
( )
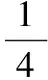
(2008年重庆市数学高考理科试题)
分析方法1回归至二次函数

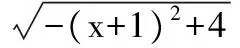
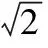
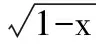
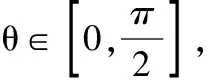
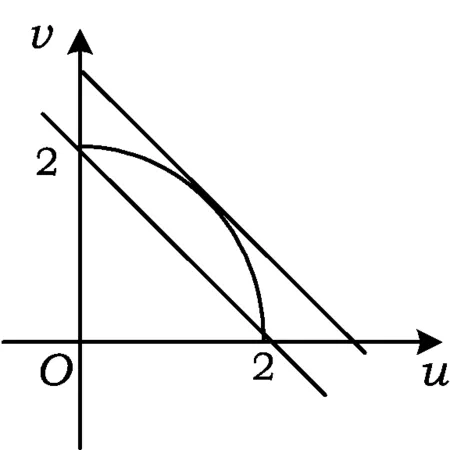
图1
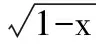
已知u≥0,v≥0且u2+v2=4,求u+v的取值范围.
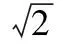
评注本题告诉我们求函数的值域方法多样,除上述方法外,本题还可采用基本不等式和柯西不等式、导数、向量等方法求函数的值域.
类型3构造函数,利用函数单调性解题
例5设a>0,b>0.
( )
A.若2a+2a=2b+3b,则a>b
B.若2a+2a=2b+3b,则a>b
C.若2a-2a=2b-3b,则a>b
D.若2a-2a=2b-3b,则a (2012年浙江省数学高考理科试题) 分析若2a+2a=2b+3b,则必有 2a+2a>2b+2b. 构造函数f(x)=2x+2x,则 f′(x)=2x·ln2+2>0 恒成立,故有函数f(x)=2x+2x在x>0上单调递增,即a>b成立.用同样的方法可排除其余选项. 例6如果cos5θ-sin5θ<7(sin3θ-cos3θ),θ∈[0,2π),那么θ的取值范围是______. (2011年全国高中数学联合竞赛一试试题) 分析题设不等式等价于 7sin3θ+sin5θ>7cos3θ+cos5θ. 因为f(x)=7x3+x5是(-∞,+∞)上的增函数,所以sinθ>cosθ,故 例7不等式log2(x2-x)<-x2+x+3的解集为______. 分析题设不等式等价于 log2(x2-x)+(x2-x)<3. 设函数f(x)=log2x+x,则f(2)=3,函数f(x)=log2x+x在(0,+∞)为增函数,即 f(x2-x) 亦即 0 解得 x∈(-1,0)∪(1,2). 评注解决此类问题的关键是从不等关系中抽象出具体的函数关系,即构造适当的函数,通过判断函数的单调性达到比较2个数大小的目的.其本质是函数单调性的定义逆用,比如函数f(x)在区间[a,b]为增函数,若对于任意的x1,x2∈[a,b],有f(x1)>f(x2),则x1>x2. 类型4相互迁移,函数奇偶性、周期性和对称性的求解方略 ( ) A.5 B.6 C.7 D.8 (2012年辽宁省数学高考试题) 图2 评注某些函数在有2条对称轴、2个对称中心或1个对称中心和1条对称轴的前提下,利用它们的抽象式可以推导出函数的周期性,如本题由题设可以得出x=0,x=1是函数的2条对称轴,之后得出了该函数的周期为2.解决此类问题的突破口是根据函数的性质得到f(x)的解析式,结合函数图像可求解. 分析方法1令t=x-1,则 f(-t+1)-2=-f(t+1)+2, 亦即 f(-t+1)+f(t+1)=4, 故 f(lg20)=-1. 方法2直接判断f(1-x)+f(1+x)=4,即函数f(x)的图像关于点(1,2)中心对称. ( ) (2008年四川省延考区数学高考试题) 评注函数的奇偶性是函数对称性的一种特殊情况.在某些特定情况下,两者可以相互转化,这也是解决函数对称性问题的一种数学思想.在高考复习中,也应该掌握常见函数对称性的抽象特征,如: (1)设a,b均为常数,函数y=f(x)对一切实数x都满足f(a+x)+f(a-x)=2b⟺函数y=f(x)的图像关于点(a,b)成中心对称图形; (4)若f(x)是定义在R上的偶函数,其图像关于直线x=a对称,则f(x)是周期函数,且2a是它的一个周期; (5)若f(x)是定义在R上的奇函数,其图像关于直线x=a对称,则f(x)是周期函数,且4a是它的一个周期; (6)若函数图像关于2条直线x=a,x=b对称,则函数y=f(x)是周期函数,且2|a-b|是它的一个周期. 另外,利用函数图像理解和研究函数的性质是应该重视的考查点之一,函数图像比函数解析式更直观,比抽象函数更具体,其包含的信息量大,对考生的数学能力要求也较高. 从近几年的数学高考试题来看,函数的“两域四性”往往与导数、数列、不等式、三角函数、解析几何等知识交汇而命制成综合问题,以体现运用函数的概念和性质去分析问题、转化问题、解决问题的能力,凸显“函数与方程思想”这一最重要、最基本的数学思想方法. ( ) A.[0,1] B.[0,1) C.[0,1)∪(1,4] D.(0,1) 2.函数f(x)的定义域为A,若x1,x2∈A且f(x1)=f(x2)时总有x1=x2,则称f(x)为单函数.例如,函数f(x)=2x+1(x∈R)是单函数.下列命题错误的是 ( ) A.函数f(x)=x2(x∈R)是单函数 B.指数函数f(x)=2x(x∈R)是单函数 C.若f(x)为单函数,x1,x2∈A且x1≠x2,则f(x1)≠f(x2) D.在定义域上具有单调性的函数一定是单函数 3.定义在R上的函数f(x)满足f(x+6)=f(x).当-3≤x<-1时,f(x)=-(x+2)2;当-1≤x<3时,f(x)=x,则f(1)+f(2)+f(3)+…+f(2 012)= ( ) A.335 B.338 C.1 678 D.2 012 4.已知y=f(x)+x2是奇函数,且f(1)=1.若g(x)=f(x)+2,则g(-1)=______. 6.定义在R上的函数f(x)在(-∞,a]上是增函数,函数y=f(x+a)是偶函数.当x1 参考答案 1.B 2.A 3.B 4.-1 6.f(2a-x1)>f(x2) 7.2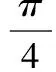

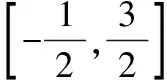
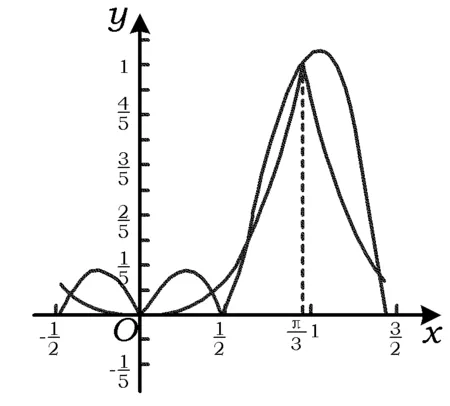

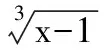

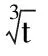
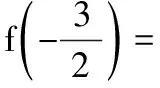




4 精题集萃