例谈三角恒等变换与解三角形的复习

● (湖州市教育科学研究中心 浙江湖州 313000)

例谈三角恒等变换与解三角形的复习

●王勇强(湖州市教育科学研究中心 浙江湖州 313000)

1 考点回顾

(1)纵看近4年的浙江省数学高考，对三角函数的考查，一般是以2个左右的客观题和1个解答题的形式出现，以中、低难度题为主.三角恒等变换是解决三角函数的图像与性质、解三角形这2类问题的重要工具，因此掌握同角三角函数的基本关系、诱导公式、两角和与差的正弦、余弦和正切公式，掌握二倍角公式并能加以运用，是解决三角函数问题的关键.解三角形是三角函数的一个典型应用，考试说明中明确提出必须掌握正弦、余弦定理，并能运用这2个定理解决实际问题.因此三角恒等变换与解三角形是三角函数部分的重要内容，也是这4年来浙江省高考必考的一个知识点.

(2)高考中三角恒等变换这部分题型灵活，主要考查运算能力、公式及其变式的灵活运用能力.在客观题中，突出考查基本公式所涉及的简单运算；解答题以中等难度题为主，重点考查三角函数名称、角、关系式的变换，多数问题都会联系三角形、向量等概念进行综合考查.正、余弦定理揭示了三角形边、角之间的数量关系.近些年，高考对正、余弦定理的考查一般集中在求解三角形的边、角、形状、面积等方面.

2 命题趋势

(1)应用两角和与差公式、倍角公式求值、化简，以及与三角函数性质、解三角形综合仍是重点，题型多样，中、低难度，是重要的得分点.三角恒等变换还经常与三角函数图像、性质、平面向量、数列等知识综合考查，在知识交汇点上命题也是目前高考的一个趋势，它体现了求新的命题思想.

(2)运用正、余弦定理解三角形是高考的重点内容之一.不仅要关注运用正、余弦定理解三角形问题，还需要关注正、余弦定理和平面向量、解析几何、三角函数等知识的综合问题，同时也不要忽视用正、余弦定理解决一些与测量和几何计算有关的实际问题.

3 典例剖析

例1在△ABC中，3个内角A,B,C,满足A∶B∶C=1∶2∶2，求1-cosA+cosB-cosAcosB的值.

(课本练习题改编)

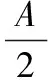
评注该题考查了正、余弦的二倍角公式的正用和逆用，特别是求2sin18°cos36°的值需要灵活的思维.三角函数是以“角”为自变量的函数，三角恒等变换一看“角”，一般可先从“角”的特征去分析，这是最重要的一环，常见思路是复角变单角、一般角变特殊角、目标角变已知角；三角恒等变换二看“函数名称”，常见的有“切化弦”、“万能公式”等；三看“结构特征”，常用思路是关系式的展开与合并、次幂的转换、分式与整式的运算、角度的配凑等.另外，在高三复习时应让学生熟悉一些特殊角的三角函数，除了30°,45°,60°外，也可适当了解15°,18°,36°,72°,75°等特殊角度的三角函数值的求法.

(1)求tanC的值；

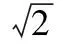
(2012年浙江省数学高考理科试题)

评注该题主要考查内角和定理、两角和的正弦公式、同角三角函数的基本关系、正弦定理、三角形面积公式等基础知识，同时考查运算求解能力.立足通性通法是浙江省高考命题一直延续的特点，在平时复习时要注重“题不在多，理解则灵”，特别是要重视对各章节知识通性通法的复习和掌握.三角函数式变形的过程就是分析矛盾、发现差异，进而消除差异的过程.在这一过程中须仔细观察式子中各项的角、函数名称及运算式子的差异，找出特征，从中找到解题的突破口.

( )

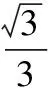
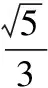
(2012年全国数学高考大纲卷理科试题)

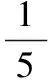
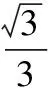
因为α为第二象限角，所以sinα>0,cosα<0,于是

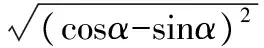
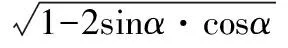
从而

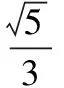
故选A.

评注函数问题首要要素是定义域，因此在解决函数问题时一定要有范围意识.本题比较典型，解法较多.在解此题时无论是转化为单角α的问题，还是转化为倍角2α的问题，都会涉及到开方，如果学生没有范围意识，常常会出现开方直接取正号的错误.这种错误看似“失误”，究其根源是对三角函数符号的意识不强、思维不严谨导致的，因此在三角恒等变换中一定要加强范围先行的意识.

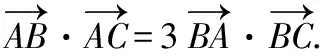
(1)求证：tanB=3tanA；

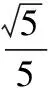
(2012年江苏省数学高考试题)

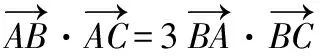
例5某同学在一次研究性学习中发现，以下5个式子的值都等于同一个常数.

①sin213°+cos217°-sin13°cos17°；

②sin215°+cos215°-sin15°cos15°；

③sin218°+cos212°-sin18°cos12°；

④sin2(-18)°+cos248°-sin(-18)°cos48°；

⑤sin2(-25)°+cos255°-sin(-25)°cos55°.

(1)试从上述5个式子中选择一个，求出这个常数；

(2)根据第(1)小题的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论.

(2012年福建省数学高考理科试题)

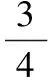
解(1)略.

(2)三角恒等式为

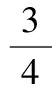
sin2α+cos2(30°-α)-sinαcos(30°-α)=

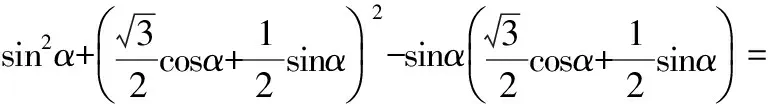
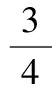
评注该题主要考查同角三角函数的基本关系式、两角和与差的三角函数公式、二倍角公式等基础知识，同时考查运算求解能力、抽象概括能力、推理论证能力，还考查了特殊与一般思想、化归与转化思想.以上将cos(30°-α)展开，再代入运算,这种解法看上去平常、普通却很有效，是“化腐朽为神奇”、“平平淡淡才是真”.三角函数公式众多，而且使用方式也是灵活多样的，因此在复习中不仅要让学生学会套用、逆用、变形使用公式，还要让学生掌握公式及其变形的特点，提高观察能力，准确判断选用，从而灵活使用公式，正确、简便地进行运算求解.

4 精题集萃

( )

( )

( )

( )

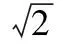
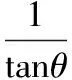
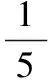
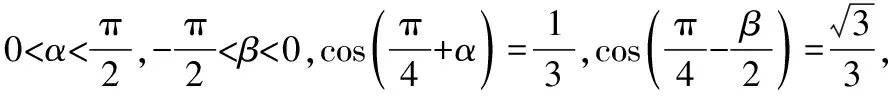
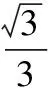
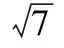
5.在△ABC中，角A,B,C所对的边分别为a,b,c.已知8b=5c，C=2B，则cosC=

( )

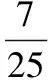
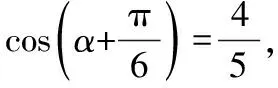
7.设△ABC的内角A,B,C所对的边为a,b,c，则下列命题正确的是______．

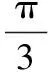
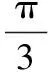
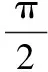
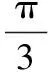
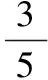
9.设△ABC的内角A,B,C的对边分别为a,b,c，且2cos(B-C)=4sinBsinC-1．

(1)求角A；

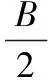
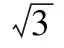
(1)求角A；

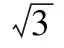
参考答案

1.A 2.D 3.C 4.B 5.A

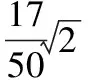
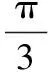
10.解(1)由正弦定理得

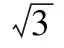
即

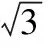
从而

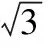
于是

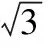
即

解得

A=60°

a2=b2+c2-2bccosA,

得

b+c=4,

从而

b=c=2.