浙江省数学高考立体几何试题的剖析和思考

●

(鲁迅中学 浙江绍兴 312000)

浙江省数学高考立体几何试题的剖析和思考

●章显联应国刚

(鲁迅中学 浙江绍兴 312000)

1 阅卷概况

笔者参加了2013年浙江省数学高考网上阅卷的评卷工作，高考评卷分为试评和正式评卷2个步骤.首先是试评，先由每道题的组长讲解该题可能出现的解法及每一种解法的评分细则，然后由每道题的阅卷者进行网上试评，每一份试卷的每一道题最少要经过2个人背对背批改.在此过程中阅卷者需达到2个统一：(1)统一解法.通过试评，各位阅卷者把试评卷中出现的新解法都汇总给组长，然后组长又统一讲解解法的逻辑性与正确性，从而使每一位阅卷者对每种解法都做到心中有数，避免考生解答正确,阅卷者错评.(2)统一评分标准.解答题的取卷方式是由电脑随机给2位阅卷者的,笔者被分配到的题是理科卷第20题(立体几何试题).若2位阅卷者给出的分数相差2分以上，则需组长或副组长等3～4位教师仲裁，2位阅卷者给出的分数无效.下面笔者就所批阅的立体几何试题进行一些总结和反思.

2 试题回顾

2013年浙江省数学高考理科试题第20题是一道立体几何题，主要考查空间点、线、面的位置关系以及二面角、空间向量的应用，同时考查空间想象能力和运算求解能力.

图1

(1)证明:PQ∥平面BCD;

(2)若二面角C-BM-D的大小为60°,求∠BDC的大小.

3 试题剖析

3.1 第(1)小题解析

本小题要证明的线面平行可转化为线线平行或面面平行，或利用空间向量(建立空间直角坐标系或用基底法).

证法1如图2，取O为BD中点，F为CD上一点，FD=3CF,则QF∥AD，且2QF=MD.又PO∥MD且2PO=MD,故QFOP为平行四边形，PQ∥OF,因此PQ∥平面BCD.

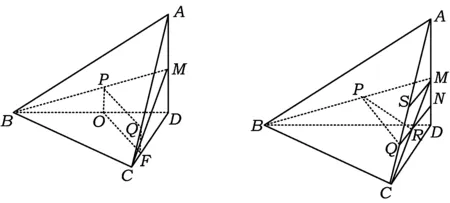
图2 图3

证法2如图3，取MC中点R，AC中点S，则QR∥SM.因为SM∥CD，所以QR∥CD.又因为PR是△MBC的中位线，所以PR∥BC，从而

△PQR∥△BCD，

于是

PQ∥△BCD.

证法3取W为MD的中点，则WA=3WD.因为AQ=3QC，所以QW∥CD.又因为PW是△MBD的中位线，所以PW∥BD，从而

△PQW∥△BCD,

故

PQ∥△BCD.

证法4延长AP交BD于点N，可以证明AP=3PN.因为AQ=3QC，所以PQ∥NC,故PQ∥△BCD.

图4

证法5如图4，延长MQ与DC延长交于点X，可以证明点Q为MX的中点.在△MBX中，PQ为△BMX的中位线，从而PQ∥BX，故PQ∥△BCD.

证法7(解析几何法)建立直角标系，点O的z轴坐标为0.5,PQ∥平面BCD.

第(1)小题出现的错误有：

(1)建系错误，比如以D为原点，以DB，DC，DA分别为x轴、y轴、z轴建立空间直角坐标系.

(2)证法1中只证明PO∥QF就得出四边形POQF为平行四边形.

(3)线面、面面平行的判定定理和性质定理掌握错误，如由PR∥BC得出△PQR∥△BCD.

3．2 第(2)小题解析

本小题正确解法有：

图5

解法1如图5，作出二面角的平面角∠HGC,求出二面角的平面角或证明CG⊥面ABD或等价形式.设∠CDB=θ,则

故

θ=60°.

解法2解析几何法(给出3种建系法).

(1)如图6，以O为原点、BD为y轴(或者以D为坐标原点、BD为y轴)建立坐标系.设平面BMC的法向量为m，则

又平面BMD的法向量为n=(1,0,0),从而

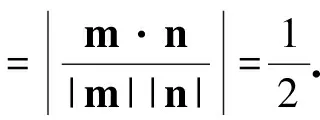
图6 图7

(2)如图7，以C为原点、CD为x轴、CB为y轴建立坐标系.平面CMB的法向量为m=(-1,0,x0),平面DMB的法向量为n=(y0,x0,0),从而

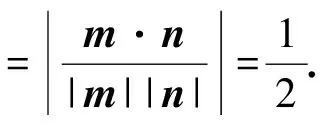
(3)以D为原点建立坐标系求解(略).

解法3利用面积射影定理求解(略).

第(2)小题的出现的错误有：

(1)利用几何法不能正确作出二面角C-BM-D的平面角.

(3)建坐标系错误.

此外，还有部分考生有大篇幅涂改、删除现象.这固然是考试时的紧张心理所致，但答题时草率上手，匆匆读完题后就急于答题，对题意不求甚解，思考不充分，必然会出现漏写、多写、错写等各种错误，只好大面积涂改.

3．3 评分再现

本题的评分策略如下：

3.3．1 注重方法，能给分时就给分

3.3．2 紧抓关键，推理到位少扣分

如为证明线面平行要化为面面平行，而证明面面平行时，关键要体现2条相交直线分别平行，然后下结论，这样得满分(6分).若只有一对直线平行，说明面面平行得2分，若没有得出结论扣2分.

4 教学启示和思考

针对该题的特点、考查意图以及考生在答题中出现的典型错误，建议高中数学的教学、复习应重视以下几个方面.

4．1 强化系统知识，提升思维水平

立体几何中涉及的概念、性质和定理比较多，但知识点之间的联系也比较紧密.学生在平时练习中要注意归纳和概括，对知识点准确把握，掌握对一类题目的常规解法，高考复习时更要不断总结反思，强化系统知识，教师则可以运用概念图或其他的知识框架帮助学生梳理知识、形成系统，把空间图形的基本位置关系以及判定定理和性质定理编制成网络.同时，还应鼓励学生一题多解，善于用不同方法解题，培养学生多角度思考问题的能力，提升思维水平，这也从另一个方面强化了知识结构.图8是立体几何定理模型集体合影：

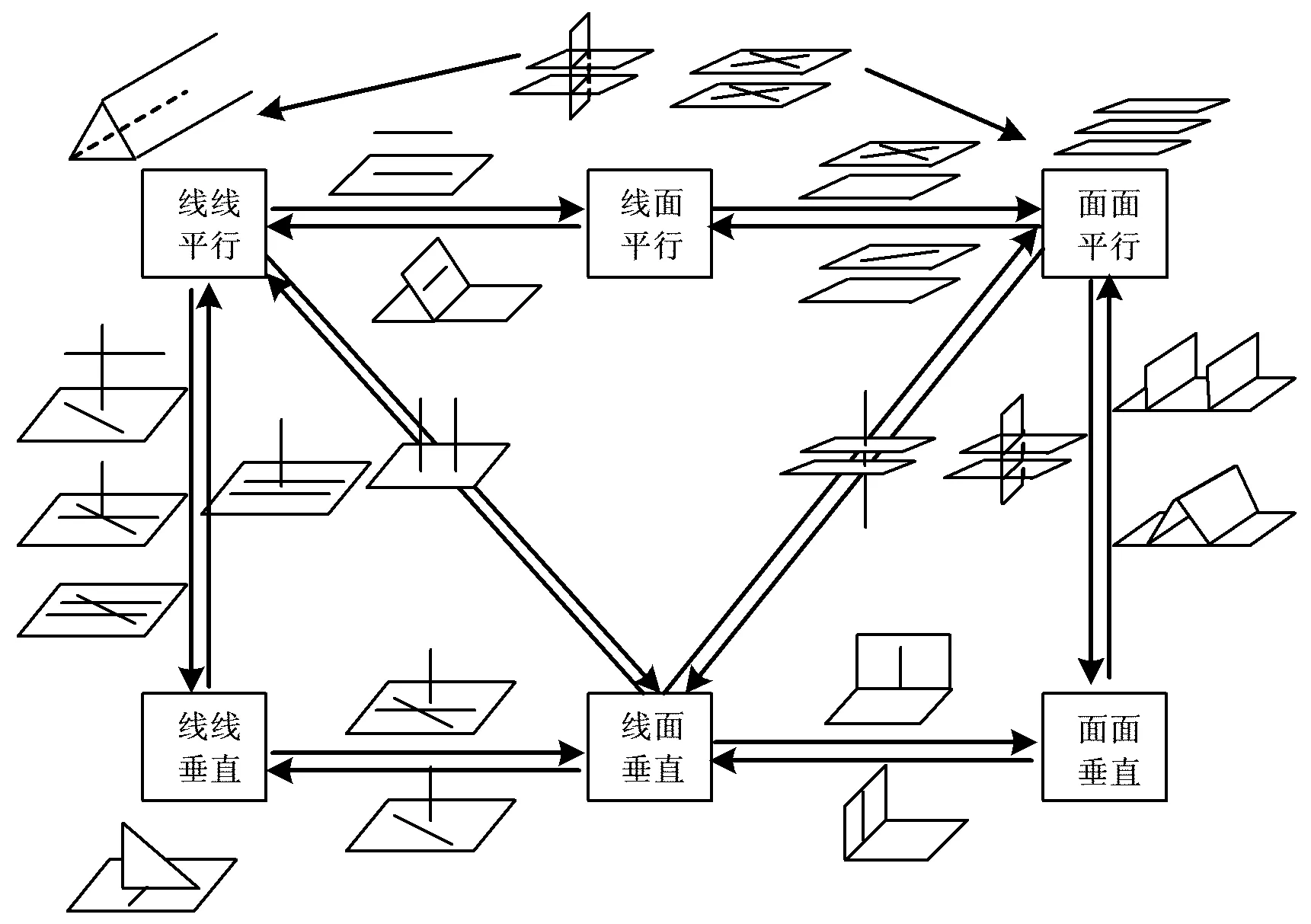
图8

4．2 重视能力培养及解法的应用，促进缜密思维

立体几何的教学过程中教师应努力培养学生的空间想象能力及逻辑推理能力.学生在学习平面几何时已经形成了初步的逻辑推理能力，但立体几何中定理的运用条件相对平面几何较多，也较为复杂，教师在教学过程中应着重强调、适当示范，并注意通过不准确或错误推理案例的警示来强化推理语言的叙写，逐步使学生养成缜密的推理习惯.解决立体几何题主要有2种方法:几何法和向量法.向量法自然地把几何问题代数化,因而在立体几何的学习中还要强化向量法.

4．3 夯实数学基础，重视解题细节

“基础不牢，地动山摇”.教师应重视常规基础题的练习，示范解题要规范,关键步骤要突出,从不起眼的解题细节抓起.只有夯实基础，学生的基本知识和基本技能才能唤起高层次的数学思维，才能解决更难的问题，很多学生在高考复习时一味追求难题、偏题，疏于对基础题的练习和叙写，结果在考试中反而容易出错，这是本末倒置的.细节决定成败，学生在答题过程中应认真细心，养成良好的答题习惯，稳步提高数学素养.

4．4 优化课堂教学,创造高效的复习课

教师要改变复习课容量过大，盲目拔高；要改变例题讲解后没有解题回顾反思；要改变课堂模式单一，热衷冷饭重炒.复习课要留有空间、时间让学生思考、说题.

总之，立体几何知识一直是高考的主干知识，是高考重要考查的内容之一.学生必须熟练掌握常见的题型及解题方法，对常见的空间几何模型要能从中寻找解题突破，同时重视推理的逻辑性、严密性，确保推理语言的正确无误.