中心球模型下EEG正问题的数值模拟

何 娟，彭 丽

(上海师范大学数理学院，上海200234)

0 引言

随着医学影像技术的发展，脑科学研究越来越受到人们的重视，并在脑疾病的临床诊断以及脑功能区域研究等方面有着重要应用，所以针对电磁场的计算问题亟待解决．根据脑电生理学知识，人体组织如大脑、肌肉及体内的磁性介质会产生微弱的电流，可由EEG(脑电图)来测量脑皮电位势V．正问题的计算是反问题研究中的一个重要环节．EEG正问题就是根据脑内神经电流源的分布情况来确定脑皮电位势 V．以往对正问题的工作采用的是单层或多层的球脑模型［1－2］、真实脑模型［3－4］、椭球脑模型［5－6］来近似人脑，再对不同的脑模型检验其数值方法．这方面的工作也相当多．但是对于数值模拟和解析解在一起讨论的工作就相当少．本文作者为了建立和分析EEG测量数据的准确性，利用球几何作为人脑模型来研究，得到原电流分量与脑皮电位势的解析关系．这类球模型便于数学上的处理，可以得到解的解析表达式，有利于各种数值方法的精度检验，具有重要的研究价值和应用背景．以往的正问题求解一般采用边界元法、差分法或有限元法，但计算效率低且程序不够灵活．作者在加权残值法的基本原理上，利用加权残值边界元法(配点法)，建立球脑模型的EEG正问题的简便快速有效算法．

1 基本方程

如果把人脑看成是一个有界的封闭电磁系统，人脑组织中的磁导率与自由空间的磁导率一致，即μ=μ0=4π ×10－7H/m．那么大脑的生理活动规律满足 Maxwell′s Equations方程组的微分形式如下［7］:

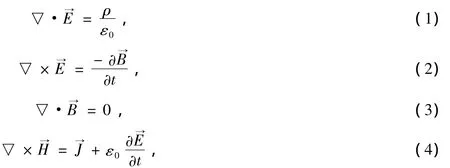
以及所谓的煤质特性方程，磁通密度与磁场强度的关系:

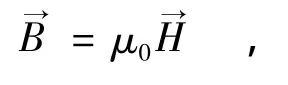
电通密度与电场强度的关系:

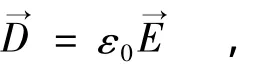
电流密度与电场强度的关系:

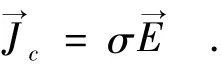
其中，ε0≈8．85×10－12F/m是自由空间的绝对介电系数，σ是电导率，t代表时间，ρ称为电荷密度函数，称为电流密度矢量．

2 脑模型

人脑Ω可以看成是一个具有分段常数电导率σ的有界导体，在脑外的电导率σ=0．把空间Ω分成Ωi，i=1，…，m个子区域，每个区域的表面记为Si．在每个Ωi内电导率σ=σi．每一层的半径记为Ri．

对方程(9)求解，运用Green公式及边界条件，得到面Sj上r点处的电位势的表达式［8］:

其中，σ0=1是自由空间中的电导率是面Si上r′处的单位外法向量分别是Si的内层和外层电导率称为原在电位势．

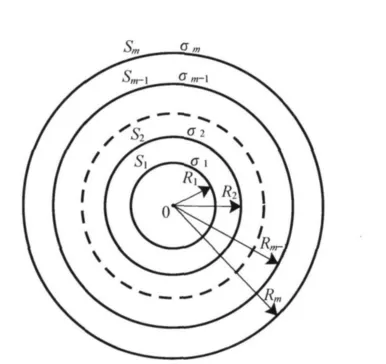
图1 一个同心圆面(人脑的平面图)

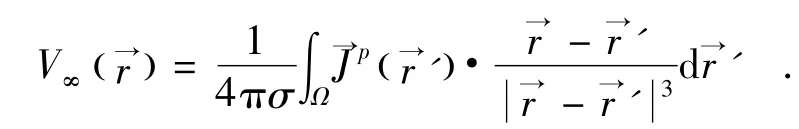
在偶极子神经电流源模型下，即假设脑内神经电流源是一个位于rq处且具有偶极距q的偶极子:)是狄利克雷函数．在此时原在电位势

为了便于计算，将方程(10)利用Vladimirov［9］的结果就有:

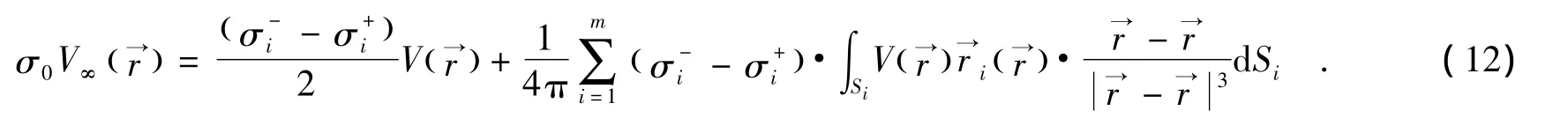
特别地，单层均匀导体中EEG正问题的场方程为:

采用如下公式定义的中心球模型去近似脑型S:x2+y2+z2=R2，S=∂Ω．其中R为球的半径，∂Ω表示有界均匀Ω的边界．

在球坐标系下，x，y，(z)的坐标可以表示成R，θ，(φ)的形式，即:

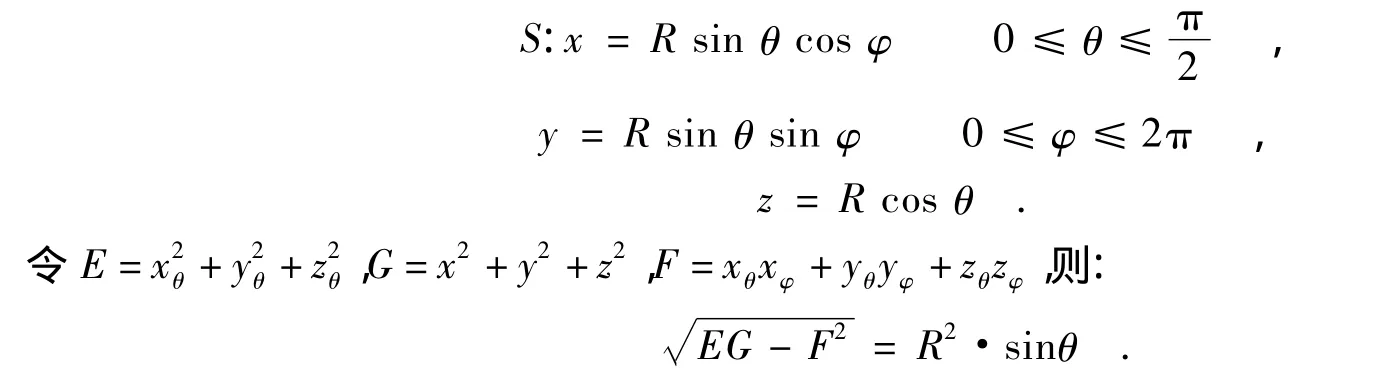
3 加权残值边界元法

加权残值边界元法是一种广泛应用于求解边界积分方程近似解的数学方法．一般常用的加权残值边界元法有配点法、子域法、最小二乘法、伽疗金法和矩法5种．使用这种方法自由度少，计算效率高，具有程序简单，工作量少和易实现等优点．下面来看EEG正问题的求解．

首先定义V(r)的线性算子:

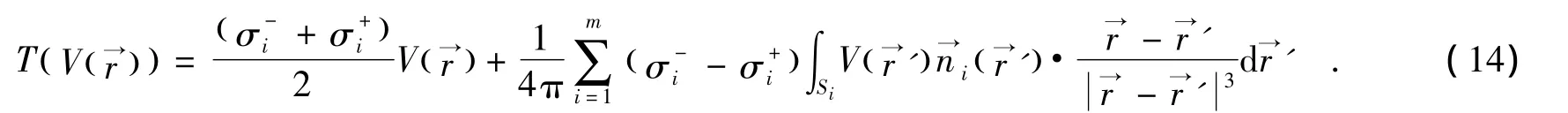
特别地，在单层均匀有界的导体中，(14)的线性算子可以简化为:

由方程(13)和(15)，即:

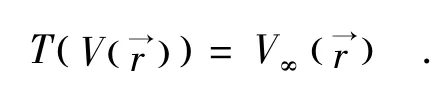
令残差:

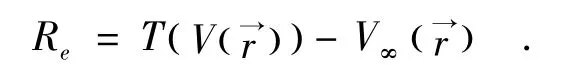
即

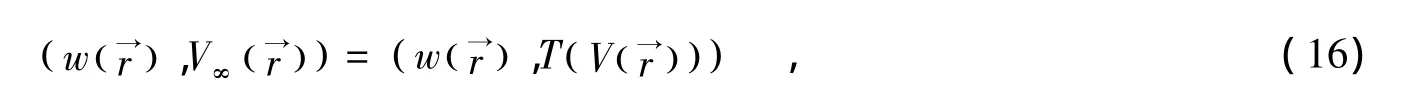
即

其中∂j为任意的系数．将(16)和(17)联立，则对每个 φj，j=1，…M，都有:

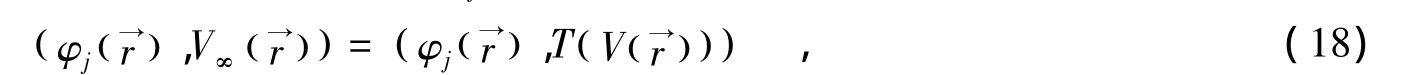
即

其中，βj是待定的参变量．将(19)代入到(18)中，T()·是一个线性算子，可得:

对权函数来说，采取不同的基底对应不同的数值方法．为了方便计算，选用加权残值边界元配点法，即为配点，那么(20)可以简化为:

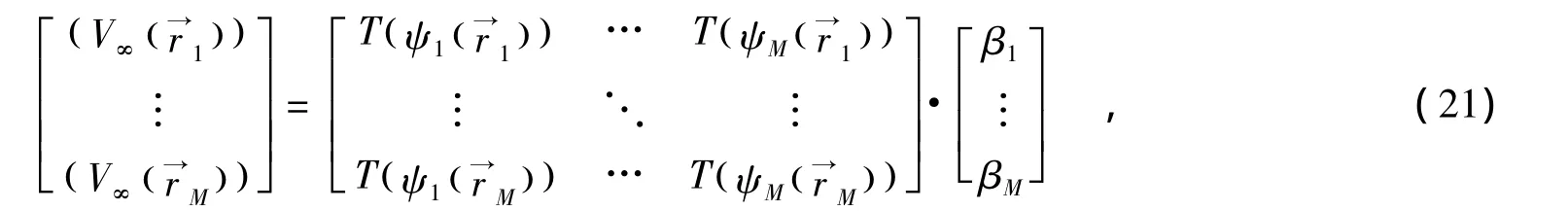
即

其中，H为M×M的矩阵，b为M×1的待定系数向量，p为M×1的向量．

4 单层中心球模型的解析解

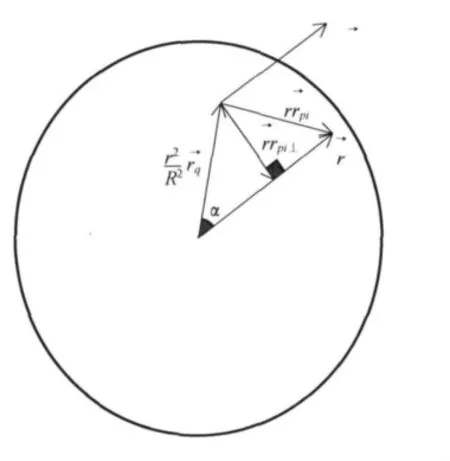
图2 rr→pi正交分解的示意图

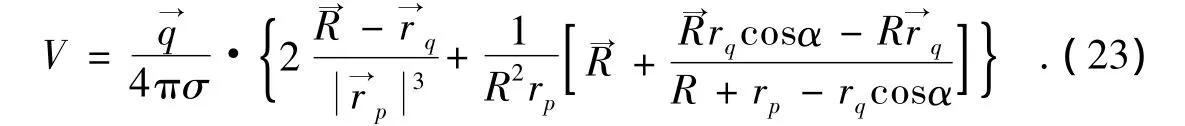
5 数值模拟及其结果

在球坐标系中，(22)的系数矩阵H中的元素:

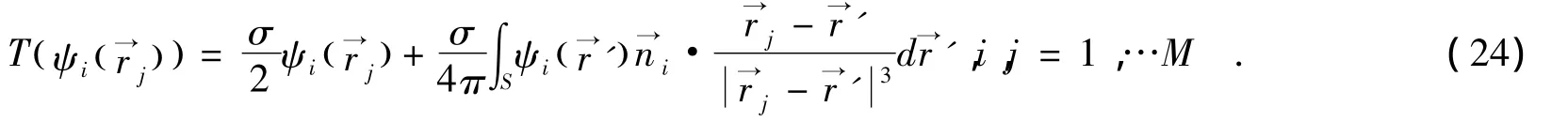
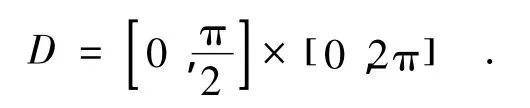
选配点为

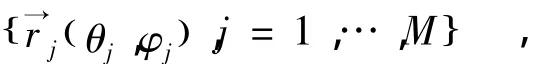
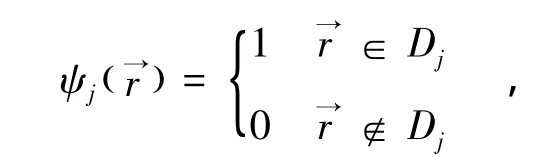
三角基底

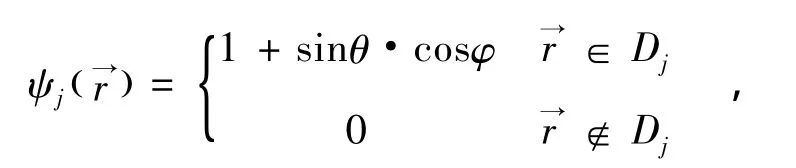
(24)变为

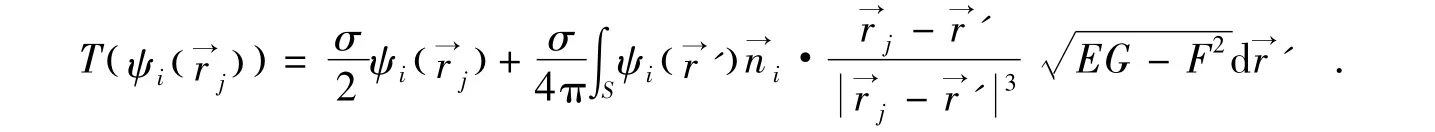
数值试验选取的参数如下:球半径R=8．7 cm，电导率σ=0．33，边界正则化参数δ=1 cm，配点个数M=100(也称配点的阶数)．为观察电位势的变化规律，选取了4个具有相同偶极矩但方向不同的偶极子:

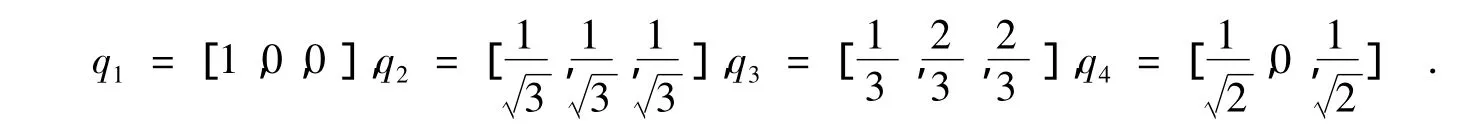
并让偶极子的位置沿着平行于z轴方向的直线从 (0 ，0，3．5 )移动到 (0 ，0，6．5)．

下面分别在三角基底和常数基底下比较电位势的精度和效率，经计算可知，数值计算中三角基底的系数矩阵H的条件数是1．6997，常数基底的系数矩阵H的条件数是1．0360．运算时间上均在80s左右．可见，此方法相较于有限元和差分法具有程序比较灵活、计算效率高、运行速度快等优点．三角基底下脑皮电位势在不同的偶极子位置和偶极子方向随配点的变化情况见图4．常数基底下脑皮电位势在不同的偶极子位置和偶极子方向随配点的变化情况见图5．

由图4和图5可以看出，在偶极子参数相同的情况下，三角基底和常数基底计算得到的脑皮电位势随配点的变化趋势是相似的，且数量级保持一致．在偶极子的方向一致的前提下，对每个偶极子的位置存在着电位势的峰值，在不同的基底下比较了电位势峰值的变化情况，结果表明变化趋势是同步的．见图6．

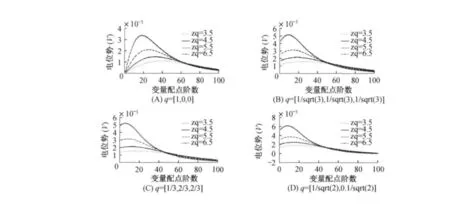
图3 V∞(r)的变化规律

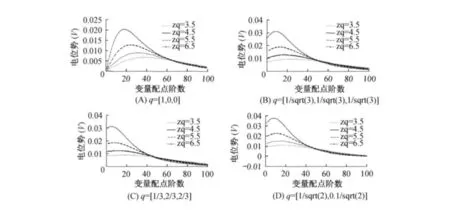
图4 三角基底下脑皮电位势的变化情况

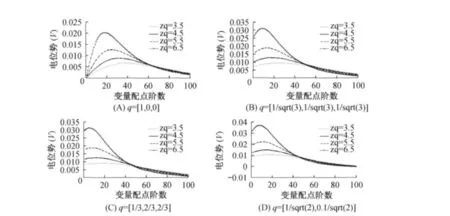
图5 常数基底下脑皮电位势的变化情况

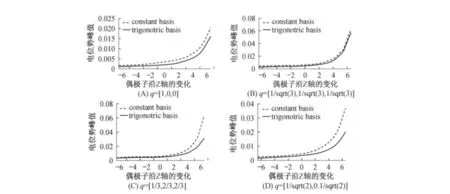
图6 不同基底下电位势峰值的变化情况

最后根据方程(23)的解析解，在数值模拟假设的相同的参数下，得到脑皮电位势随着配点的变化情况如图7:

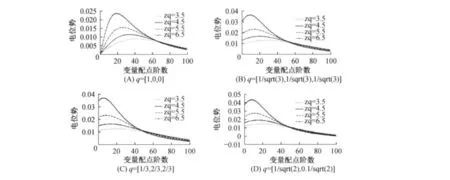
图7 脑皮电位势随配点的变化情况

通过图4、图5与图7，将数值解与解析解进行比较，结果表明脑皮电位势的变化趋势是相同的，同时在个方向下，脑皮电位势的峰值都在配点阶数10～20之间，得到的均是2～3个数量级，且三角基底优于常数基底．

6 结论

通过对中心球模型下EEG正问题的数值解与解析解的讨论，运用加权残值边界元(配点法)进行数值模拟，观察到不同偶极子参数，在常数基底函数和三角基底函数下脑皮电位势的变化情况相似，且均在同一个数量级．当偶极子参数相同时，通过图4、图5、图7比较可知，从运算效率和计算精度来看，三角基底优于常数基底，在EEG正问题的计算中占有明显的优势．这种方法在椭球脑模型和多层球脑模型也可进行类似的讨论．

［1］MUNK J C，PETERSM J．A fast method to compute the potential in the multisphere model［J］．IEEE Trans Biomed Eng，1993，40(11):1166 －1174．

［2］ZHANG Z．A fast method to compute surface potentials generated by dipole within multilayer anisotropic sphere［J］．Phys Med Biol，1995，40(3):335 －349．

［3］FLETCHER D J，Amir A，Jewett D L，et al．Improved method for computation of potentials in a realistic head shape model［J］．IEEE Trans Biomed Eng，1995，42(11):1094 －1104．

［4］MEIJSJW H，WEIER O W，PETERSM J，et al．On the numerical accuracy of the boundary element method［J］．IEEE Trans Biomed Eng，1989，36(10):1038 －1049．

［5］CUFFIN B N．Effects of head shapes on EEG’s and MEG’s［J］．IEEE Trans Biomed Eng，1990，37(1):15 －22．

［6］SAMUEL K L，NUNEZ PL，WIJESINGHE R S．High －resolution EEG using spline generated surface laplacians on spherical and ellipsoidal surfaces［J］．IEEE Trans Biomed Eng，1993，40(2):145 －153．

［7］刘岚，黄秋组．电磁场与电磁波基础［M］．2版．北京:电子工业出版社，2000．

［8］SARBASJ．Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem［J］．PhysMedBiol，1987，32(1)，11 －22．

［9］VLADIMIROV V S．Equations of mathematical physics［M］．New York:Marcel Dekker，1971．

［10］YAO D Z．Electric potential produced by a dipole in a homogeneous conducting sphere［J］．IEEE Transactions on Biomedical Engineering，2000，47(7):947 －949．