两条圆锥曲线的一种相互转化方法

福建省泉州五中 杨苍洲 （邮编：362000）福建省安溪一中 王志良 （邮编：362400）

（Ⅰ） 求 直 线AA1与直线A2B交点M的轨迹方程；

（Ⅱ）设动圆C1：x2＋y2＝与C0相交于A′、B′、C′、D′四点，其中b＜t2＜a，t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等.证明＋为定值.

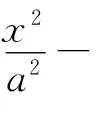
1 从椭圆到双曲线

一般化上述命题，可得：

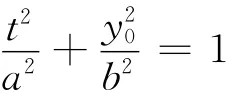
又知A1（－a，0），A2（a，0），则

直线P1A1的方程为

直线P2A2的方程为

2 从双曲线到椭圆

从椭圆类比到双曲线可得：

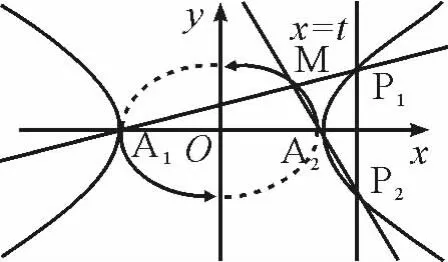
命题2 已知动直线x＝t与双曲线C：

相交于P1、P2两点，点A1、A2分别为双曲线C的左，右顶点，则直线P1A1与直线P2A2交点M的轨迹方程为

证明过程可以仿照命题1，这里从略.

3 从抛物线到抛物线

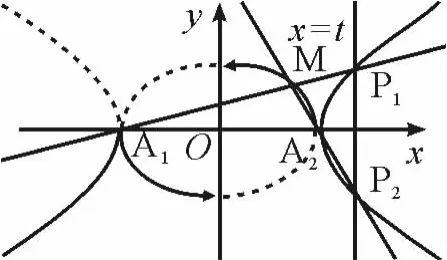
上述的两个命题都涉及了有心圆锥曲线的两个顶点，而抛物线的顶点只有一个，是否还能进行类比呢？回答是肯定的，抛物线的另一个顶点可视为无穷远处，因此，这里我们可以用一条“平行于对称轴的直线”来代替上述命题中的“P2A2”.

命题3 已知动直线x＝t与抛物线C：y2＝2px（p＞0）相交于P1、P2两点，点O为抛物线C的顶点，过P2作直线l平行于x轴，直线P1O与直线l的交点M的轨迹方程为y2＝－2px（y＜0）或y2＝－2px（y＞0）.