基于混合策略的差分进化算法

梁 静，周钦亚，瞿博阳，宋 慧

(1.郑州大学 电气工程学院，河南 郑州450001;2.中原工学院电子信息学院，河南郑州450007)

0 引言

最优化是人们在实际生活中经常遇到的问题，它们可以通过数学方法抽象成函数求最优解问题.随着实际工程中的问题从线性到非线性的转变，出现复杂性增加，极值增多以及建模困难等问题，智能优化算法已经逐渐成为相关学科的一个主要研究目标和研究方向.因此，大量国内外学者对智能优化算法进行了研究改进.

在文献［1］中作者通过对个体进行分工来提高算法的性能.文献［2］采用随机向量和最优向量作为基准向量，它们的权值分别为和，通过改变大小来提高算法的性能.文献［3］使用种群中心作为基准向量并在种群中心产生变异个体.文献［4］把种群分为三个子种群，每个子种群采用不同的策略并且在不同的时期分配不等的个体.Qin等［5］采用4种变异策略，同时对不同策略采用不同的交叉因子CR，并且CR通过一个自适应机制进行调整.文献［6］按照个体适应度的差异将个体分成不同的子种群，并针对不同的个体适应度值采用不同的变异因子，保证在加快算法收敛速度的同时能够跳出局部最优点.在文献［7］中Brest等人给出了自适应控制参数的差分进化算法，在算法迭代过程中引入4个在0和1之间均匀分布的随机数，由它们控制变异因子和交叉因子的产生.

笔者提出了一种混合策略差分进化算法，该算法通过种群中个体的适应度大小将种群分为3个大小不同的子种群，而每个子种群的大小根据当前总种群的收敛情况而定.为了提高算法的通用性和稳定性，每个子种群使用不同的变异策略以及不同的控制参数，对适应度好的子种群使用有利于局部搜索的策略和参数，对适应度不好的子种群使用有利于全局搜索的策略和参数.

1 标准差分进化算法及其分析

差分进化算法也是智能优化算法中的一种，由Storn和Price于1997年提出［8］，该算法最初的目的是为了解决切比雪夫多项式问题.算法采用实数编码方式，利用种群中个体间的差分向量对个体进行方向扰动，实现个体变异，再通过交叉和选择操作以达到对个体的函数值进行优化的目的.差分进化算法同遗传算法一样包括变异、交叉以及选择操作，但相比于遗传算法，DE算法的选择操作采用一对一的淘汰机制来更新种群.从本质上说，DE算法是一种基于实数编码的具有保优思想的贪婪遗传算法.

智能优化算法主要解决的是传统优化算法不能解决的非线性优化问题.非线性最小化优化问题描述如下:

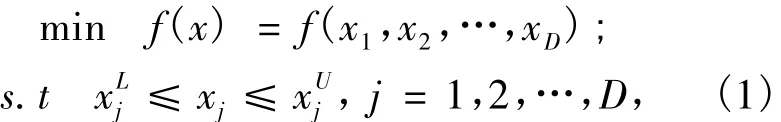
算法首先在所求问题的可行解空间中随机产生初始种群P(G)={x1(G)，x2(G)，…，xNP(G)}，G=0，NP 为种群大小.

对第G代中的每一个个体xi进行变异操作，得到与其相对应的变异个体vi，即

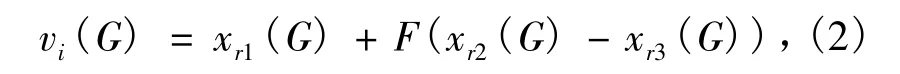
式中:r1，r2，r3∈{1，2，…，NP} 是3个互异的整数且不同于i，F是变异因子，为固定实数，取值范围一般是［0，2］.

对每个个体和与其对应的变异个体实施交叉操作，生成实验个体Ui(G)，即

式中:rand表示［0，1］之间的随机数;CR是交叉概率，取值范围是［0，1］;jrand表示{1，2，…，D} 中的随机整数.

对超出搜索范围的实验个体Ui(G)做如下处理

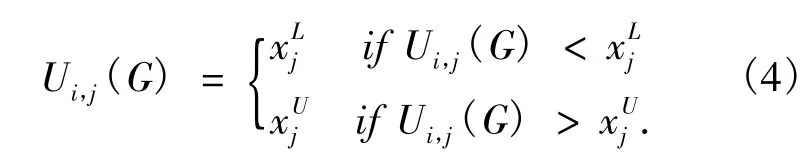
将实验向量Ui(G)与目标向量xi(G)的目标函数值进行比较，选择较优的个体进入下一代，选择操作如下

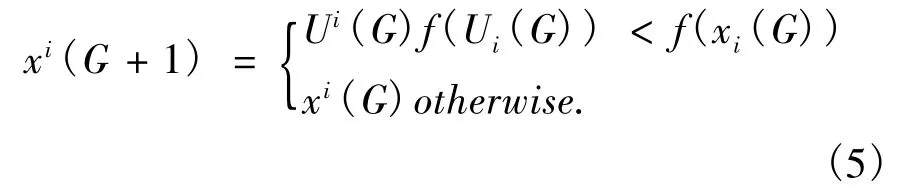
目前针对差分进化算法的变异操作提出了十余种不同的变异策略.每种策略具有不同的作用，有些策略全局搜索能力比较强;有些策略局部搜索能力比较强，收敛速度比较快，收敛精度比较高;有些策略可以很好的协调种群的全局搜索能力和局部搜索能力.同样差分进化算法的控制参数对于算法的优化结果也有着很大的影响.DE算法主要参数包括种群的大小NP，变异因子F，交叉概率CR.如果种群NP太小会使搜索的范围受到限制，导致搜索不到全局最优解，而种群太大会产生大量无效搜索.当F较大时，种群具有较好的多样性，反之，如果F较小，种群将会在当前个体很小范围内进行搜索，可以增加种群的收敛速度.较大的CR使得产生的实验个体与目标个体之间存在较大差别，对于保持种群的多样性和全局搜索是有利的，较小的CR则有利于种群的局部搜索和收敛速度.

2 算法描述

根据已有的研究成果提出一种混合策略的差分进化算法.该算法的基本思想是根据适应度将种群分为3个大小不同的子种群:优种群、劣种群以及一般种群.其中适应度较好的个体组成优种群，该种群负责局部搜索，提高算法的收敛速度和精度;适应度较差的个体组成劣种群，该种群的作用就是进行全局搜索，使算法跳出局部最优，避免算法早熟;其余的个体组成一般种群，该种群的作用就是平衡算法的全局搜索能力和局部搜索能力.

3个子种群的大小将会根据总种群是否陷入局部最优来设定.当种群陷入到局部最优时，需要增大劣种群以便加强全局搜索能力从而跳出局部最优.种群是否陷入局部最优根据粒子的适应度标准差和粒子间距离标准差来判断.因为在正常情况下粒子随着算法的进行将会逐渐收敛到一起，它们的适应度标准差以及它们之间的距离标准差都会越来越小.反之，如果在某些时刻粒子的适应度标准差很小而距离的标准差很大则可以说明粒子已经陷入局部最优，这是由于一些函数在最优值附近存在大量对称的局部最优所造成的.算法同时还采用变化的控制参数，这样算法能够有效的进行局部搜索和全局搜索.

优种群的作用是进行局部搜索，因此选取DE/best/2/bin作为该子种群的变异策略，该模式以当前种群最好的个体为基准个体，再加上2个随机扰动向量，在当前最好个体的周围进行搜索，具有很好的局部搜索能力;劣种群的作用是进行全局搜索，所以该种群的变异策略选取DE/current-rand/2/bin，该策略以自身为基准个体，加上2个随机扰动，具有很强的全局搜索能力;一般种群选取DE/current-best/2/bin作为变异策略，以自身为基准个体，通过向当前种群最优个体进行学习，能够有效的平衡差分进化算法的全局搜索能力和局部搜索能力.3个变异策略如下所示:

优种群V=Xbest+F(Xr1-Xr2+Xr3-Xr4);

劣种群V=Xi+F(Xr1-Xi+Xr2-Xi);

一般种群V=Xi+F(Xbest-Xi+Xr1-Xr2).

优种群的变异因子F取为0.5，既不影响该子种群的收敛，又降低了该子种群陷入到局部最优的概率，CR 取为0.1［4］.劣种群的 F 在1［4］和0.7之间随机选择，CR采用0.9［4］，使该种群在保持种群多样性的同时还可以进行局部搜索.一般种群作为平衡优种群和劣种群的中间种群，其控制参数应该选取范围应该在优种群和劣种群中间，因此，F在0.5、0.7、1之间随机选择，CR取为0.7，其中F随机选择的规则是:在每次选择操作进行后，如果子代的适应度劣于父代的适应度，那么F在各自的取值范围内随机选取一个值作为下次迭代的值.

3 算法仿真分析

为验证笔者所提出的混合策略差分进化算法的有效性，下面通过4个典型的标准函数:schaffer(f1)、rosenbrock(f2)、rastrigin(f3)和griewank(f4) 进行仿真实验.其中，函数f1的最优值是1，在距离理论最优值大约3.14的范围内存在无限多的局部最优点.函数f2的最优值附近存在一个大峡谷，算法很容易陷入里面.f3和f4均是多峰值函数，在它们的搜索范围内存在大量局部最优点.后面3个函数最优值都是0，4个测试函数的表达式如下:

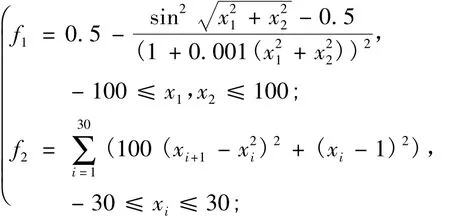
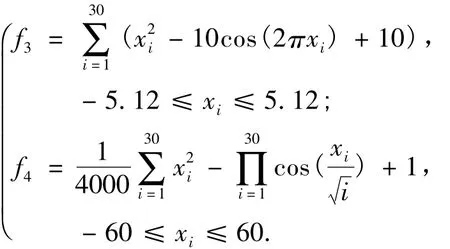
将本算法记为 HSDE，并与标准遗传算法(SGA)［9］、采用DE/rand/1/bin策略的DE算法［9］、采用 DE/rand-best/1/bin 策略的DE［9］、采用DE/best/1/bin策略的 DE算法［10］、动态调整子种群个体的 DE算法(NPDE)［10］、双种群伪并行DE算法(DSPPDE)［9］和动态多种群并行 DE算法(DMPDE)［4］进行比较.

对算法的改进不仅是要求找到函数的最优值，而且要保证算法的效率.因此，如果需要对几种算法进行比较，可以有两种比较方式，比较常见的就是保持种群的大小以及迭代次数一样，另外一种是保持评价次数一样，这样算法可以在搜寻最优值的同时不会降低算法的效率，它们所达到的效果是一样的.笔者参考文献［9］中所给的参数，对其中的参数进行一定的修改，其它参数不变.笔者将NP全部设置为原文献中NP的一半，将它们的迭代次数翻倍，和原文献的评价次数一样大.每个函数运行30次，通过平均值和标准差进行比较，平均值可以看出算法的搜索能力，标准差可以看出算法的稳定性，比较结果如表1所示.

从表1中可以看出，标准遗传算法搜索到的结果距离理论最优值还有很大的距离，尤其是对于第二个函数的优化结果显示算法的收敛精度和稳定性很差.使用单一策略的标准差分进化算法和标准遗传算法相比，采用DE/rand/1/bin的DE算法对第三个函数的优化结果跟遗传算法相差比较大，稳定性也不是太好，采用DE/best/1/bin的DE算法对第三个函数的优化结果略劣于遗传算法，其余的在收敛精度和稳定性上均有不同程度的提高.3个单一策略相比采用DE/rand-best/1/bin的DE算法的优化结果最好，其余2个分别是全局搜索和局部搜索，从中可以看出算法只有兼顾全局搜索和局部搜索才能有比较好的结果.NPDE、DSPPDE和DMPDE算法相较于前面4个算法，从它们的优化结果可以看到这3个算法在收敛精度和稳定性上都有了很大的提高.笔者提出的HSDE算法通过将种群分为3个大小不等的子种群并且每个种群使用不同的变异策略、变异因子和交叉概率，使种群随时保持最好的全局搜索能力和局部搜索能力.从结果可以看出算法对函数的优化结果有了很大的提升，除了第二个函数以外，其它3个均可以找到理论最优，而且第二个函数的优化结果相比较于其它的算法也有了很大的提高.

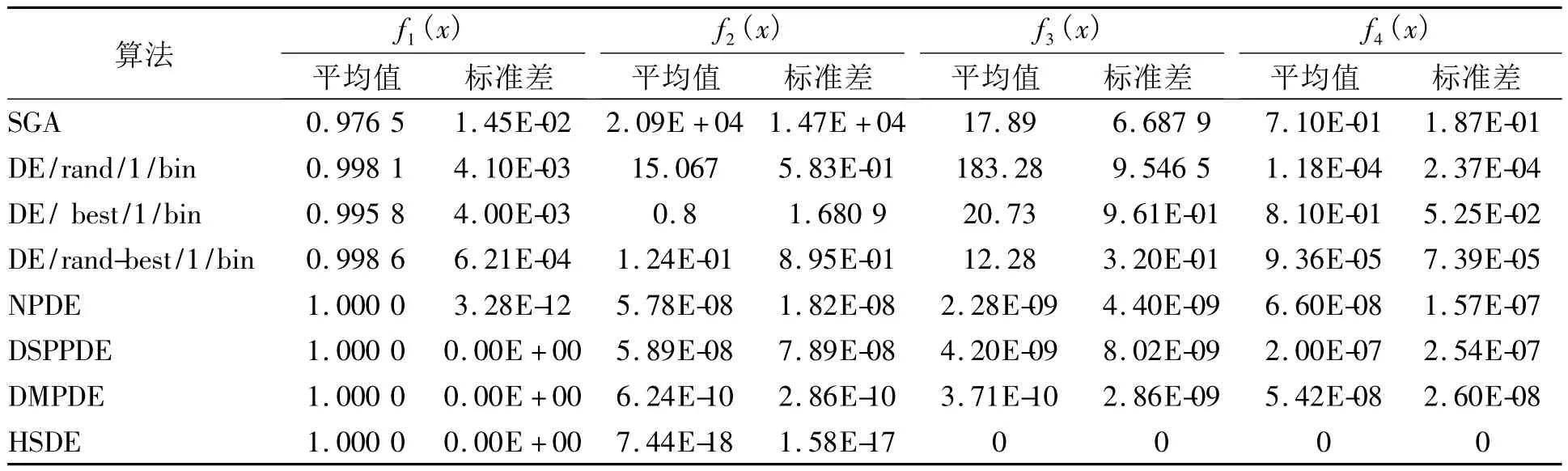
表1 8种算法对4个测试函数的实验结果Tab.1 Experiment results of four test functions under eight algorithms

4 结论

针对传统差分进化算法易早熟收敛的现象，提出一种混合策略差分进化算法.该算法利用粒子适应度将种群分为多个子种群，每个种群使用不同的策略，同时根据粒子适应度标准差和粒子距离标准差判定每个种群的大小，同时每个种群还使用不同的变异因子和交叉概率，保证种群在搜索的过程中一直能够保持最好的全局搜索能力和局部搜索能力.从仿真结果看以看到，笔者的算法具有更强的稳定性、通用性和收敛精度.

［1］姜立强，刘光斌，郭铮.分工差分进化算法［J］.小型微型计算机系统，2009，30(7):1302-1304.

［2］高岳林，刘俊梅.一种带有随机变异的动态差分进化算法［J］.计算应用，2009，29(10):2719-1922.

［3］池元成，方杰，蔡国飙.中心变异差分进化算法［J］.系统工程与电子技术，2010，32(5):1105-1108.

［4］龙文.一种改进的动态多种群并行差分进化算法［J］.计算机应用研究，2012，29(7):2429-2431.

［5］QIN A K，HUANG V L，SUGANTHAN P N.Differential evolution algorithm with strategy adaptation for global numerical optimization［J］.IEEE Transactions on Evolutionary Computation.2009，13(2):398-417.

［6］卢峰，高立群.基于多种群的自适应差分进化算法［J］.东北大学学报:自然科学版，2010，31(11):1538-1541.

［7］BREST J，GREINER S，BOSKOVIC B，et al.Self-A-dapting control parameters in differential evolution:a comparative study on numerical benchmark problems［J］.IEEE Transactions on Evolutionary Computation.2006，10(6):646-657.

［8］STORN R，PRICE K.Differential evolution-a simple and efficient adaptive scheme for global optimization over continuous spaces［J］.Journal of Global Optimization.1997，11(4):341-359.

［9］吴亮红，王耀南，周少武，等.双群体伪并行差分进化算法研究及应用［J］.控制理论与应用，2007，24(3):453-458.

［10］徐松金，龙文.调整子种群个体的差分进化算法［J］.计算机应用，2011，31(11):3101-3103.