基于人工鱼群算法的电力系统稳定器参数优化研究

刘宪林，乔云飞

(郑州大学 电气工程学院，河南 郑州450001)

0 引言

随着电网规模的不断扩大，电网间的互联日益密切，加上大机组和高快励磁装置的普遍采用，使得低频振荡现象时有发生，严重影响电网的动态稳定性.电力系统稳定器(PSS)［1-6］利用相位超前补偿环节来补偿由励磁系统带来的相位滞后，从而增加系统的动态阻尼，提高系统的稳定性.PSS作为一种抑制低频振荡最有效且经济的措施在电力系统中已经得到广泛应用.

常用的PSS参数设计方法有经典相位补偿法、数学规划法、神经网络控制理论法和人工智能算法［7-10］等.其中不少是采用单机无穷大系统中由经典调节理论得出的概念，而且采用离线整定，在多机系统中并不严格，实际工程中应用价值不高.近年来，智能算法逐渐应用到了电力系统的各个方面，常用的生物智能算法有遗传算法(GA)、人工鱼群算法(AFSA)、蚁群算法(ACO)、粒子群算法(PSO)等等.生物智能算法具有使用灵活，原理简单，编程易实现，寻优过程自适应能力好、鲁棒性强等特点.文献［9］基于改进遗传算法对多机系统PSS参数进行优化，并考虑了多种运行工况，算例结果表明算法可行.但该方法在算子的选择上较为传统，算法耗时较长，易陷入早熟，优化效果并不明显.文献［10］将人工鱼群算法应用于多机系统PSS参数优化，算例结果也证明了基本人工鱼群算法在PSS参数优化中的有效性，但此文献中系统机电振荡模式的相关信息不够详细，且缺乏对加装PSS后系统小扰动稳定性的仿真验证.

笔者采用人工鱼群算法对电力系统稳定器参数进行全局协调优化，用MATLAB编制人工鱼群算法优化程序和相关小扰动稳定程序.为了加快算法的收敛速度，提高算法的效率和可靠性，笔者借鉴其他学者的一些改进策略，对算法中的步长和视野作出了调整，并且加入了变异机制.

1 研究对象的描述

1.1 系统模型

笔者研究的问题属于小干扰稳定问题，求解此类问题的一般方法是将系统的动态特性方程在运行点处线性化，即可得到用于分析小干扰稳定问题的数学模型，方程表述为

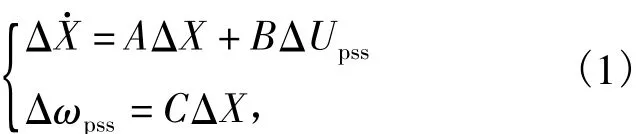
式中:ΔX为状态变量;Δωpss为 PSS的输入;ΔUpss为PSS的输出.

1.2 PSS模型

笔者所采用的PSS模型如图1所示.其中框①为PSS的增益环节，Kpss为增益系数;框②为测量环节，TR为时间常数，取0.02 s;框③为隔直环节，时间常数为TS，取TS为5 s;框④为相位补偿环节，T1为超前时间常数，T2为滞后时间常数，n为所需相位补偿环节的阶数;输入信号为角速度偏差量Δω;ΔUpss为PSS的输出.待优化变量为框①中的Kpss、框④中的T1和T2.

图1 PSS模型Fig.1 Model of PSS

1.3 目标函数

通常用机电模式下的阻尼比作为衡量PSS对低频振荡抑制效果的标准，一般要求阻尼比不小于0.05.在此情况下PSS参数优化的目标是，决定全部PSS的参数，使得在所考虑的运行方式下关于低频振荡模式的最小阻尼比达到最大，因此目标函数定义如下

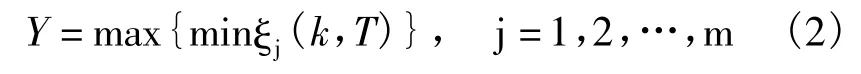
其中:kmin≤k≤kmax，Tmin≤T≤Tmax.

式中:ξj为系统第 j个低频振荡模式 λj=σj+iωj的阻尼比;m为低频振荡模式个数;k为pss增益的集合;T为pss时间常数的集合.

2 算法描述

人工鱼群算法是基于鱼群行为的仿生智能算法，2002年由李晓磊、钱积新等人提出［11］.其基本思想是:在一片水域中鱼群数量最大的地方一般就是该水域中食物浓度最大的地方，个体鱼在觅食的过程中会逐渐发现该区域并在此活动.根据这一特点，就可以模仿鱼群的各种行为，实现对全局的最优搜寻.一般认为，人工鱼群算法具有全局性好，脱离局部最优解能力强，对算法的初值参数设置要求不敏感，鲁棒性强等特点.

人工鱼群算法采用自下而上的设计方法，即从个体人工鱼的行为开始描述最后映射到整个鱼群的行为过程.相关定义为:向量X=(x1，x2，…，xn)表示个体鱼的当前位置，xi(i=1，2，…，n)为目标向量的一个因素分量，即需优化的参数，n为个体鱼状态的空间维数;Y=f(x)表示个体鱼当前位置的食物浓度，即优化问题的目标函数值;di，j=‖Xi-Xj‖表示个体鱼之间的距离.Visual为个体鱼的感知视野范围;Step表示个体鱼每次移动的步长;δ表示拥挤度因子.

人工鱼的典型行为可总结为下面几种:觅食行为、聚群行为、追尾行为和随机行为.

(1)觅食行为 设人工鱼当前位置为xi，在其感知范围内随机找寻另一位置xj.若在求极大值问题中Yi＜Yj(或在极小值问题中Yi＞Yj，极大值和极小值问题可以互换，下文均以极大值问题进行讨论)，则向该位置前进一步，否则重新选取xj，判断是否满足前进条件，若反复重复Ntry次后仍不满足，则随机移动一步.

(2)聚群行为 设人工鱼当前位置为xi，搜索当前邻域内(di，j＜Visual)伙伴数目 nf并计算其中心位置xc和食物浓度Yc.若Yc/nf＞δYi，则表明伙伴中心有较多食物且不太拥挤，就朝中心位置移动一步，否则执行觅食行为.

(3)追尾行为 设人工鱼当前位置为xi，个体鱼会在其感知邻域内知道其伙伴数目nf并且确定食物浓度最大的人工鱼位置xj.若Yj/nf＞δYi，表明xj处有较多的食物且不太拥挤，就向该伙伴方向前进一步，否则执行觅食行为.

(4)随机行为 属于觅食行为的缺省行为.人工鱼在其视野范围内随机选择一个状态并向其移动一步.

在算法中设立一个公告板，用以记录当前最佳的人工鱼位置和该位置的浓度.人工鱼在执行完每个行为后，将当前位置的食物浓度与公告板上的食物浓度进行比较，如果自身状态优于公告板状态，则用当前状态替代公告板状态.

3 算法的改进

3.1 人工鱼群算法的改进

笔者结合文献对基本人工鱼群算法作了改进［12］.

(1)视野和步长的调整

为了提高算法寻优的效率，对算法的视野和步长进行调整的原则是:在算法初期，设定较大的视野范围和移动步长，以提高算法全局搜索能力;在算法后期设定较小的视野和步长，以达到在局部范围内精确最优解的搜寻目的.其动态表达式为

式中:Stepmin和Visualmin分别表示步长和视野的最小值;Step0和Visual0分别表示步长和视野的初值;n为算法当前迭代次数;MAXGEN为设定的迭代次数上限.这样，算法中的视野和步长会随着算法的进程不断变化，以适应算法不同阶段寻优的要求.

(2)变异机制的引入

当人工鱼在多次进行觅食、聚群、追尾等行为后，公告板中的目标函数仍没有更新，则认为人工鱼达到了变异的条件.变异行为可表述为:用公告板上当前状态对应的最优个体鱼替换当前鱼群最差个体鱼，此个体鱼进行高斯变异，而鱼群中的其他个体鱼进行差分变异.

高斯变异公式表述为

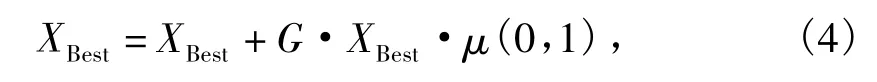
式中:XBest为当前鱼群最优状态;G为变异算子;μ(0，1)为服从均值为0、方差为1的高斯分布.

差分变异公式表示为

式中:Xi为第i条鱼的状态;F为变异算子;Xi1和Xi2为不同于Xi的两个个体鱼.

高斯变异可以提高鱼群在最优值附近的寻优精度，差分变异可以加快算法的收敛速度，同时也使算法跳出局部极值的能力大大提高.

3.2 初始人工鱼群的选取

笔者按照文献［13］介绍的基于K阵的等值法进行PSS初始参数的设计，而初始人工鱼种群在此整定值上下50%的区间范围内进行随机选取，从而有效缓解算法早熟、收敛速度慢等问题.利用基于K阵的等值法设计PSS参数.

1)列出所有发电机、负荷等元件的状态方程并在运行点处线性化，得到多机系统线性化系数矩阵 K1～K6，其形式为

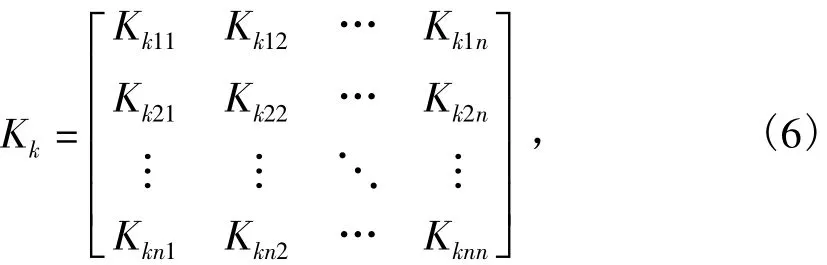
其中 k=1，2，…，6.

2)取K1～K6对角线元素Ki11～Ki66代替单机无穷大系统中发电机模型［14］线性化系数 K1～K6.

3)基于等值单机无穷大系统线性化模型采用经典相位补偿法［15］设计PSS.

4 流程图设计

利用MATLAB汇编语言进行优化程序的编制和调试，以式(2)作为人工鱼群算法的目标函数，以PSS参数 Kpss、T1、T2作为待优化变量，以规定迭代次数上限和目标函数值趋于稳定作为衡量算法收敛与否的双重标准.其设计流程如图2所示.

5 算例分析

以中国电科院8机系统为例来验证人工鱼群算法的有效性.该系统的接线图和详细参数可参照文献［16］.在计算中发电机采用三阶模型，励磁系统采用一阶惯性环节，负荷采用恒定阻抗代替.

人工鱼群算法中取初始人工鱼条数N=50，迭代上限 Genmax=30，视野 Visual0=2.85，步长Step0=1.25，试探次数Trynumber=5，拥挤度因子δ=0.06.

此系统在未装设PSS时的机电振荡模式和对应该模式的阻尼比、振荡频率和强相关机组编号如表1所示.(按机电模式阻尼比从小到大的顺序排列)

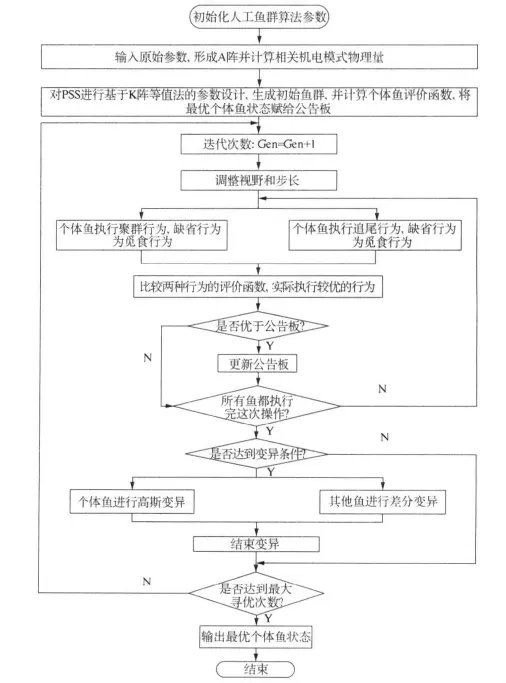
图2 人工鱼群算法优化PSS参数设计流程图Fig.2 The flow chart of design of PSS parameter with AFSA

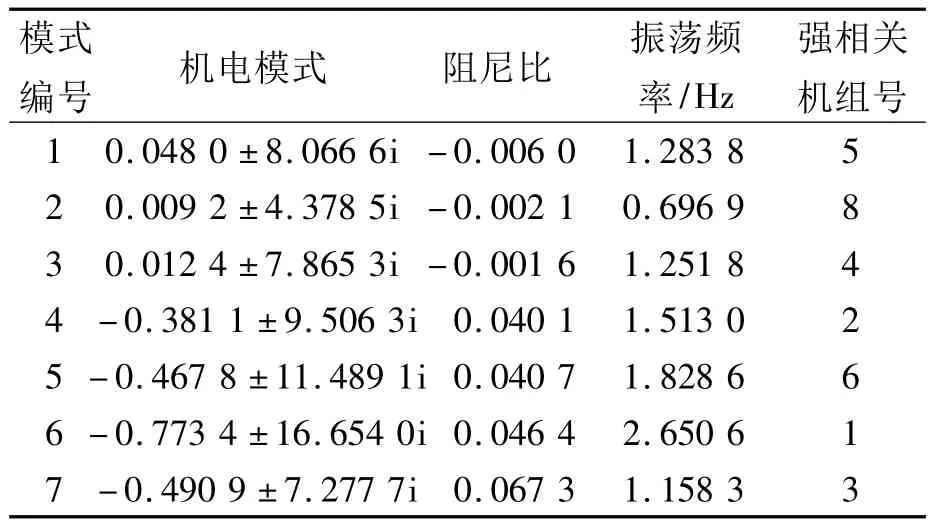
表1 系统无PSS的机电模式信息Tab.1 Electromechanical modes of system without PSS

显然，从表中可以看出，除了编号为7的机电模式，其他模式的阻尼比均小于5%的最小阻尼比要求，编号为1、2、3的3个模式甚至出现了负阻尼现象，需要加装PSS.

笔者决定在8台发电机上全部加装PSS.表2和表3分别为基于K阵等值法设计的PSS参数和加装PSS后8机系统的机电模式相关信息.

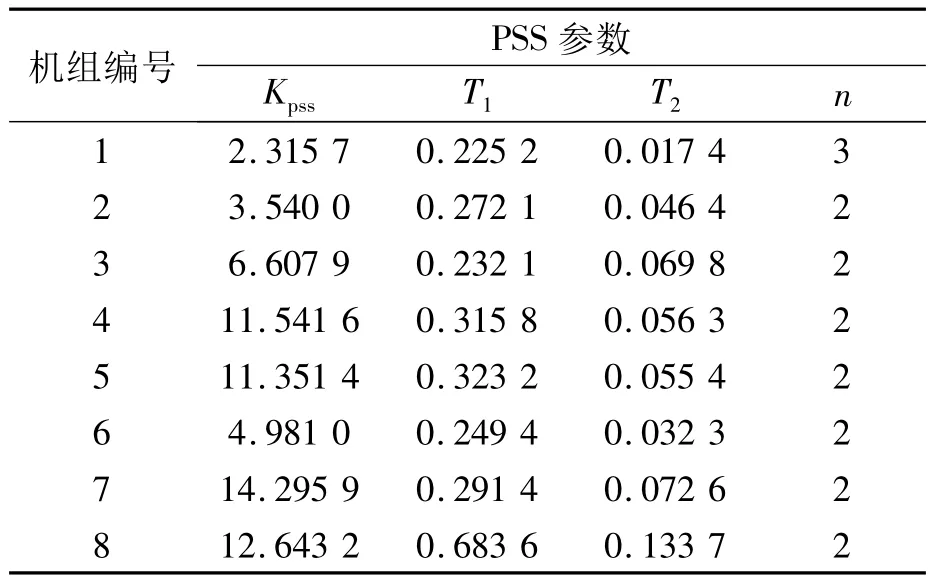
表2 基于K阵等值法设计的PSS参数Tab.2 PSS parameter with the equivalence method of K matrix

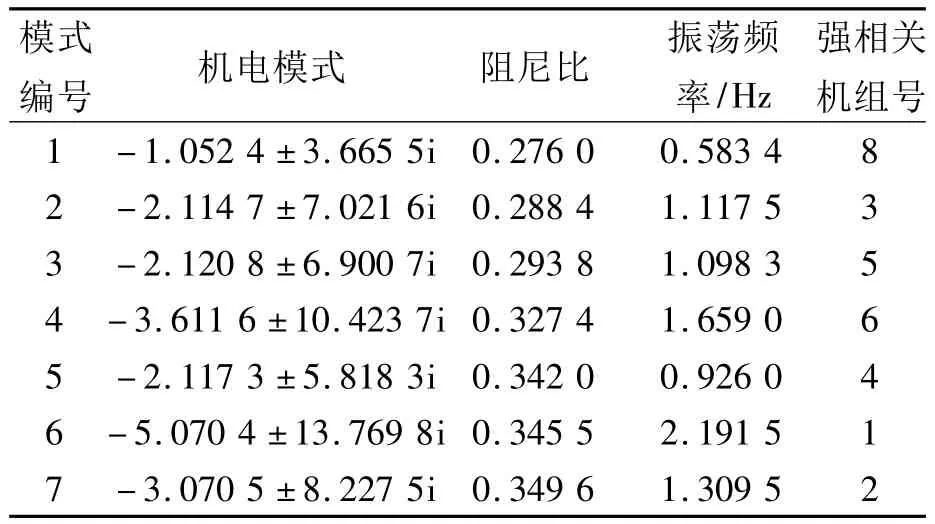
表3 基于K阵等值法设计PSS后系统的机电模式Tab.3 Electromechanical modes of system with PSS based on the equivalence method of K matrix

由表2可知，除1号机组需要加装具有3阶相位补偿环节的PSS外，其他机组加装的PSS相位补偿环节阶数都为2;而由表3可知，基于K阵等值法设计 PSS后系统的最小阻尼比 ξmin=0.276 0.以此PSS参数作为人工鱼群算法初始鱼群的选取基准，采用设计的人工鱼群算法对PSS参数进行优化.优化后的PSS参数和系统机电模式信息如表4、表5所示.

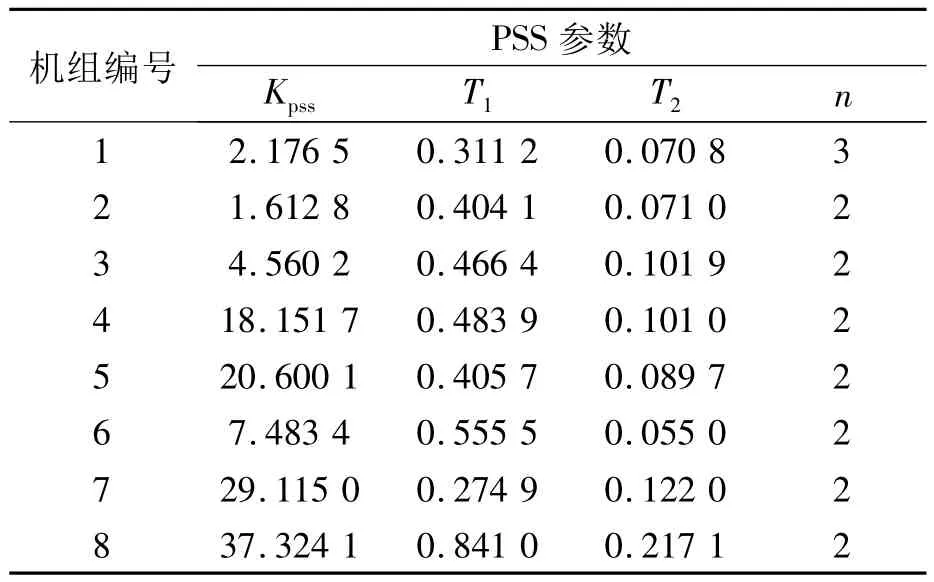
表4 人工鱼群算法优化后的PSS参数Tab.4 PSS parameter with the equivalence method of K matrix

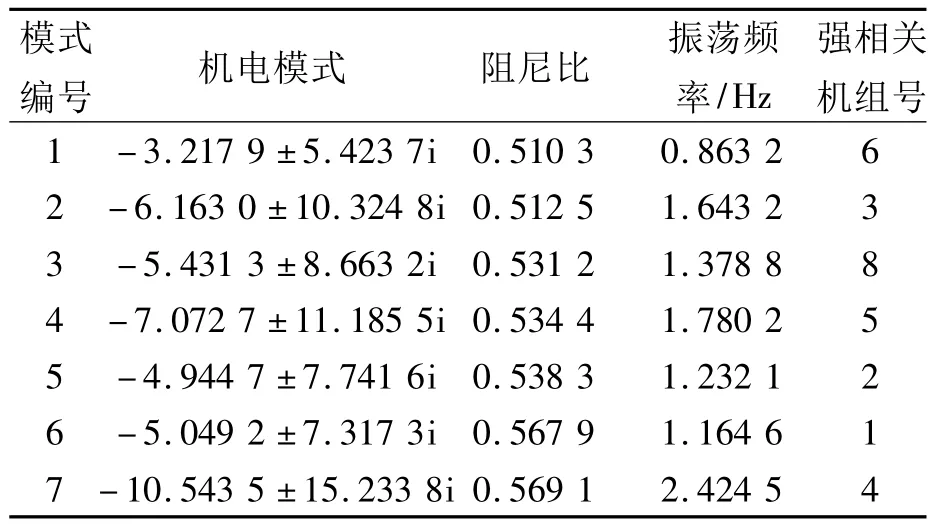
表5 人工鱼群算法优化PSS后系统的机电模式Tab.5 Electromechanical modes of system with PSS based on AFSA

笔者所设计的人工鱼群算法优化PSS参数的目标函数收敛过程如图3所示.

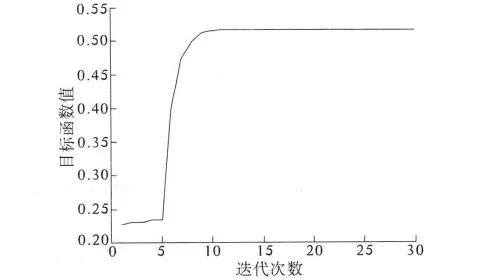
图3 人工鱼群算法优化收敛过程图Fig.3 The process chart of the optimization with AFSA

由图3可见，目标函数即最小阻尼比随着迭代次数的增加逐渐上升直至收敛，上升过程平滑稳定，无跳跃现象;目标函数值在算法迭代10次左右便已达到收敛值，最优适应值ξmin=0.51，与优化前基于K阵设计PSS的阻尼比ξmin=0.27相比，优化效果明显.上述结论均可证明笔者所设计算法的有效性.

最后，对上述8机系统进行了自由响应仿真.图4为无PSS和PSS经人工鱼群算法优化后两种情况下5#、4#和2#机相对于8#机的功角增量曲线.

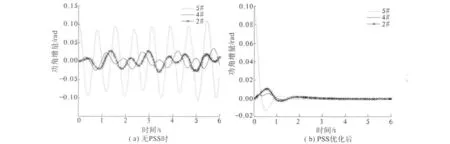
图4 Δδ的自由响应曲线Fig.4 The free response curves of Δδ

6 结论

采用人工鱼群算法对多机系统PSS参数进行全局协调优化，并对所得结果进行小扰动稳定性分析和仿真验证.为了提高算法的运行效率和收敛速度，对算法的步长和视野作出了调整，加入了变异机制，并且用基于K阵等值法设计的PSS参数作为算法初始鱼群的选取基准.结果表明:经人工鱼群算法优化参数后的PSS能够有效抑制电力系统低频振荡，提高系统的动态稳定特性.但该算法对于复杂大系统的PSS参数优化效果还有待于进一步地研究.

［1］方思立，朱方.电力系统稳定器的原理及其应用［M］.北京:中国电力出版社，1996:40-63.

［2］赵书强，常鲜戎，贺仁睦，等.PSS控制过程中的借阻尼现象与负阻尼效应［J］.中国电机工程学报，2004，24(5):7-11.

［3］M A A.Robust design of multimachine power system stabilizers using simulated annealing［J］.IEEE Trans.Enemy Conversion.2000，15(3):297-304.

［4］陈晓东.电力系统稳定器设计.［D］山东:山东大学电力系统及其自动化，2006.

［5］ROUCO L，PEREZ I J.Multi-area analysis of small signal stability in large electric power system by SMA［J］.IEEE Trans on PWRS，1993，8(3):1257-1265.

［6］邱磊，王克文，李奎奎，等.多频段PSS结构设计和参数协调［J］.电力系统保护与控制，2011，39(5):102-107.

［7］DUBEY M.Design of genetic algorithm based fuzzy logic power system stabilizers in multimachine power system［C］.Power System Technology and IEEE Power India Conference，2008.

［8］ABIDO M A.Optimal design of power system stabilizers using particle swarm optimization［J］.IEEE Trans on Energy Conversion，2002，17(3):406-413.

［9］闫健杰，赵书强，崔小磊，等.基于改进遗传算法的多机系统PSS参数协调优化［J］.华北电力大学学报，2006，33(2):16-20.

［10］胡晓波，杨利民，陈中，等.基于人工鱼群算法的PSS参数优化［J］.电力自动化设备，2009，29(2):47-50.

［11］李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式:鱼群算法［J］.系统工程理论与实践，2002，22(11):32-38.

［12］曲良东，何登旭.混合变异算子的人工鱼群算法［J］.计算机工程与应用，2008，44(35):50-52.

［13］贾继灏，马丽丽，刘宪林，等.基于等值单机无穷大系统的多机系统PSS设计［J］.电力系统保护与控制，2009，37(23):70-74.

［14］倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析［M］.北京:清华大学出版社，2002.

［15］余耀南.动态电力系统［M］.何大愚，刘肇旭，周孝信，译.北京:水利水电出版社，1985.

［16］谢志棠，宗秀红，钟志勇，等.计及FACTS装置的概率特征根分析［J］.电力自动化设备，2004，24(8):13-17.