多SP轮函数对广义Feistel结构安全性影响分析
王田丽,黄 坤
(华北水利水电大学数学与信息科学学院,河南郑州450046)
0 引言
广义Feistel结构是由郑玉良等人于1989年的美洲密码年会上提出的一系列算法结构.Lesamnta[1]是进入NIST举办的SHA-3竞赛第一轮的56个杂凑函数之一,它采用了比较流行的Type-1广义 Feistel[2]结构的变体.2010 年,Bouillaguet等人对其给出了一个20轮的积分区分器[3].2009年,Mendel等人介绍了一种分析杂凑函数的新技术,称为反弹攻击[4].在2011年的 FSE会议上,Sasaki等人将这一技术用于Feistel-SP结构的算法,给出了11轮已知密钥区分器[5].后来,Sasaki等人又将复杂度加以改进,并应用于Camellia[6].但这种技术对广义Feistel结构进行攻击的结果如何,现在还不明晰.笔者从多SP轮函数的角度出发,分析这种设计会给安全性带来什么样的影响.
1 基础知识
1.1 Type-1广义Feistel结构和Lesamnta简介
Type-1广义Feistel结构的状态有四个字,而Lesamnta的压缩函数利用分组密码和MMO结构,整个Lesamnta杂凑函数采用MD结构.对于Lesamnta-256杂凑函数,消息填充之后长度是256比特的整数倍,并被分成256比特大小的块M1‖M2‖…‖MN.记压缩函数为 CF:{0,1}256×{0,1}256→{0,1}256,它按照下列方式进行迭代:
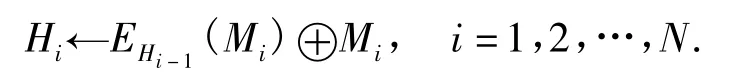
初始状态记为H0.最后的HN即为消息M的杂凑值.中间的分组密码EK为4分支的Type-1广义Feistel结构.首先,中间链值Hi-1进入密钥生成算法,生成每一轮的64比特子密钥kj,其中0≤j≤31.状态中 4 个 64 比特的字我们用 Wj,Xj,Yj,Zj来表示,则EK的输出按照下列方式计算:

轮函数F包含4个运算:轮密钥加、字节代换、行移位层、列混淆层.攻击是在已知密钥状态下,在这里忽略密钥扩展算法,细节参考文献[1].
1.2 反弹攻击
反弹攻击[4]是Mendel等人提出的一种针对杂凑函数的分析方法.它从两个状态出发,选择截断差分,在中间某S盒层构造匹配,再分别向前向后构造截断差分路径,故命名为反弹攻击.此类攻击的方法与传统的差分攻击有所不同,其关键点之一在于研究S盒层的匹配性质.
2 多SP轮函数Type-1广义Feistel结构安全性
利用三轮匹配技术,对两轮扩散(AES类)的SP轮函数的Type-1广义Feistel结构进行分析.
情形1:两轮扩散的双SP结构.如果函数采用双SP结构,并且两轮达到全扩散,则可以采用如图1的弹入结构进行攻击.图中0表示不活跃的字,F表示全活跃的字,H表示经过 P(或者P-1)达到全活跃的字.首先在#A处取一个活跃状态,此状态经过一个P扩散后全活跃,同样在#B处选择一个活跃状态,经过一个P-1扩散后全活跃,两个状态进行3轮匹配,如图1中粗线所示.而#A沿虚线运算经过一个逆SP层,然后异或轮子密钥,在第二轮异或常数,在第五轮异或轮子密钥,再进行双SP运算,如果设定第二轮的常数等于第一轮与第五轮轮密钥的异或,则可保证在第五轮异或的时候将差分消除,得到一个非活跃字.
弹出部分是概率为1的,具体每一轮的差分字特征见表1.弹出部分一共11轮,故攻击一共有16轮.
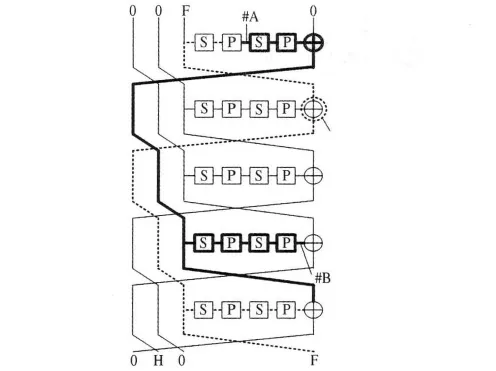
图1 Type-1双SP结构弹入攻击部分Fig.1 Inbound phase for Type-1 double SP constructure

表1 Type-1双SP结构与三SP结构弹出攻击部分Tab.1 Outbound phase for Type-1 double SP constructur and three SP structure
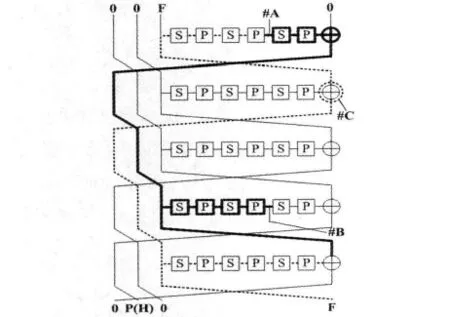
图2 Type-1三SP结构弹入攻击部分Fig.2 Inbound phase for Type-1 three SP constructure
情形2:2轮扩散的三SP结构.这种轮函数使用了3轮的SP结构,这样看起来会使得扩散更加充分,但是总的攻击仍然可以达到16轮.如图2所示,其弹出部分见表1.
其它情形:由上述两种情形可以看到,即使再增加轮数,对攻击弹入部分的影响也只是将弹入五轮之后的第二个字变为F,这样会将正向弹出部分轮数变为3轮,总的攻击轮数变为13轮.
3 Lesamnta-256的截断差分区分器
3.1 弹入部分
步骤1:(正向起始)选择并固定状态#4的两个灰色字节的差分,此差分线性地传播至状态#5,使得状态#5中有4个字节差分不为0.由于此状态第1行的每一个字节与其右下方的字节进入同一个超级S盒,将这两个字节看做一个整体,取遍其216个值,每个值均可以独立地计算至状态#9,然后存储在一个表中.这样,由状态#5至状态#9可以建立4个这样的表,每一个的大小为216.
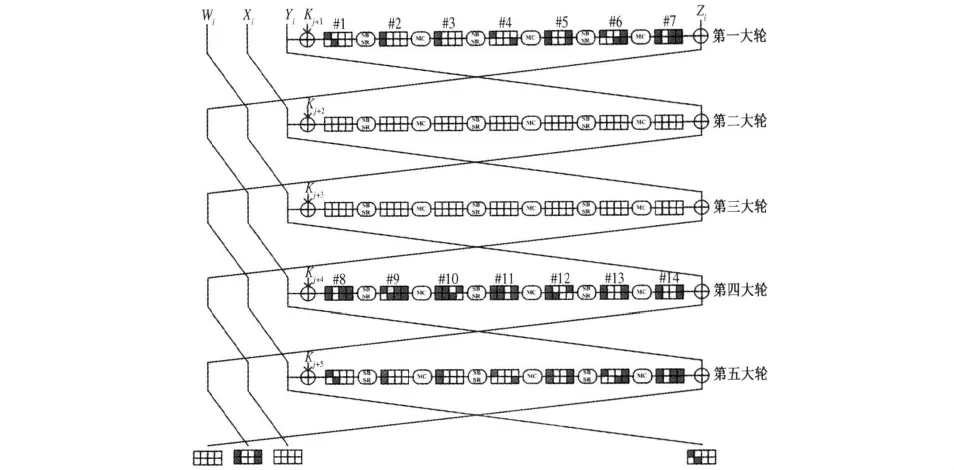
图3 弹入部分Fig.3 Inbound phase
步骤2:(逆向起始)相似地,在状态#12选择并固定4个灰色字节的差分,在状态#11取遍每一个超级S盒的输入的值,在状态#9建立4个大小为216的表.值得注意的是,在状态#9,由状态#5开始建立的每一个表都对应第1行的一个字节和它左下方的一个字节,由状态#11开始的每一个表都对应一列的两个字节.为了区别,我们从左到右记正向的四个表为 l1,l2,l3,l4,逆向的四个表记
步骤3:(匹配轮)状态#9左下角字节差分为0,取定此字节的值.这样,相当于给集合限定了216个条件,而集合中包含216个元素,我们期望在其中找到一个满足条件.这样,状态#9和状态#10的第一行的两个字节的差分和值就都确定了.而随着状态#9左上角字节的差分和值的确定,相当于给集合l1限定了216个条件,我们同样期望有一个元素满足条件.而集合l1涉及的另一个字节为#9右下角的字节,所以这一字节的差分和值也确定了.这样,我们对集合限定了216个条件,我们期望从此集合中得到一个元素满足条件.按照同样的方法,我们可以确定剩下的字节的差分和值.状态#9中第1行的第2个字节是最后确定的元素.但是,我们发现此字节的差分为零,这样就在最后多出了28个条件.开始选择状态中左下角的元素值时,也有28个选择.这样,我们便以28的时间复杂度达到了匹配.
步骤4:(正向逆向弹出)找到匹配之后,状态#4逆向传播到状态#1,状态#12正向传播到状态#14.
步骤5:(消除轮)我们发现,第4大轮输出的最后一个字,和第5大轮F函数的输出都是由同样的截断差分模式生成的.而且,状态#1的差分与第5大轮第一个状态的差分相同,值相差一个常数.记第2大轮的F函数的输出为,则相差的常数可以表示为
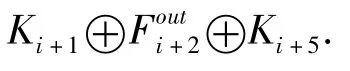
通过上述步骤,我们得到了一条包含5大轮的差分路径.此路径的时间复杂度由两部分组成:建8个表的时间复杂度和中间匹配的时间复杂度.共用218.6次S盒的计算的时间,和218个“两字节”的存储.
3.2 弹出部分
事实上,弹出部分可以分为两个部分:正向弹出部分和逆向弹出部分.共有19轮,具体细节见表2.

表2 19轮截断差分路径Tab.2 19-round truncated differential path
3.3 与理想置换进行区分
用218.6次S盒的计算的时间,218个“两字节”的存储,构造了一条输入输出均有2224种可能差分的差分路径.我们的攻击为19轮,每轮有24次的S盒计算,故时间复杂度为218.6/19×24=29.8.而状态含32个字节,故存储为218/32=213.而一个理想置换,如果找到具有同样差分模式的两个输入/输出的话,需要232/2=216的计算复杂度.所以,此区分器可以将19轮的Lesamnta置换与理想函数有效区分.
4 结论
得到了Type-1广义Feistel-SPSP结构的16轮已知密钥区分器,Type-1广义Feistel-SPSPSP结构的16轮已知密钥区分器.并证明了即使轮函数使用更多的SP迭代,也可以构造至少13轮的已知密钥区分器.还将这一方法应用与杂凑函数Lesamnta,如何通过其构造碰撞或者近似碰撞值得进一步研究.
[1]SHOICHI H,HIDENORI K,HIROTAKA Y.SHA-3 Proposal:Lesamnta[EB/OL].http://ehash.iaik.tugraz.at/uploads/5/5c/Lesamnta.pdf.
[2]ZHENG Yu-liang,MATSUMOTO T,IMAI H.On the construction of block ciphers provably secure and not relying on any unproved hypotheses[C]//Proceeding of CRYPTO.Santa Barbara,USA,1989:461-480.
[3]CHARLES B,ORR D,GAËTAN L P.Attacks on hash functions nased on generalized feistel:application to reduced-round lesamnta and SHAvite-3512[C]//Proceeding of Selected Areas in Cryptography.Waterloo,Ontario,Canada,2010:18-35.
[4]MARIO L,FLORIAN M,CHRISTIAN R,et al.Rebound distinguishers:results on the full whirlpool compression function[C]//Proceeding of ASIACRYPT.Tokyo,Japan.2009:126-143.
[5]SASAKI Y.Meet-in-the-Middle Preimage Attacks on AES Hashing Modes and an Application to Whirlpool[C]//Proceeding of Fast Software Encryption.Lyngby,Denmark.2011:378-396.
[6]SASAKI Y,EMAMI S,HONG D,et al.Improved known-key distinguishers on feistel-SP ciphers and application to camellia[C]//Proceeding of Information Security and Privacy.Wollongong,NSW,Australia.2012:87-100.

