轻量级分组密码Midori64的积分攻击

连 闯 毛 明 李艳俊

1(西安电子科技大学通信工程学院 陕西 西安 710071)2(北京电子科技学院 北京100070)3(北京电子科技学院信息安全系 北京 100070 )

0 引 言

物联网技术的快速发展已经使其成为新时代信息技术的重要组成部分。物联网最初是通过射频识别、红外感应和定位系统等信息传感设备把物品与互联网连接起来。因此设备体积变小成为行业内追逐的趋势,这使轻量级密码算法成为了研究的热点。这些年研究人员设计了许多轻量级分组密码如：MIBS[1]、PRESENT[2]、Lblock[3]、Piccolo[4]、GOST[5]等。这些算法大都可以在保证足够的安全性下实现良好的效率,为物联网信息传递过程中的信息加密提供了保障。Midori[6]是在2015年ASIACRYPT会议上提出的一种轻量级分组密码,其分组长度为64和128 bit,分别记为Midori64和Midori128。Midori算法的密钥长度为128 bit,可以提供较好的安全性。

积分分析起源于Square攻击。在Square攻击的基础上，Lucks[7]攻击了Feistel结构型分组密码Twofish算法，并因此提出了Satuation攻击。Biryukov等[8]通过分析SPN结构安全性,提出了Multiset攻击。Knudsen总结了Square攻击、Saturation攻击和Multiset攻击,并在此基础上提出了积分攻击。

目前,密码学者利用积分攻击分析了Rijndael[9]、ARIA[10]、Camellia等[11]著名算法的安全性。积分攻击对AES、MISTY等算法的攻击结果优于已有的差分分析和线性分析结果。

对Midori的攻击主要有不可能差分分析[12]、基于轮密钥猜测的不可能差分分析[13]、抗故障攻击[14]等。还没有针对Midori算法的积分攻击,在对算法模块进行深入分析后,本文首先提出了Midori64算法的4轮积分区分器,并向解密方向扩展1轮,得到了5轮高阶积分区分器。使用5轮积分区分器对Midori64进行了6轮、7轮和8轮的攻击,并给出了攻击的数据和时间复杂度。

1 Midori64算法描述

Midori算法是一种SPN结构的轻量级加密算法。算法明文分组长度64 bit,轮数为16轮,种子密钥长度为128 bit,其运算单元为半字节。以下所称字节均表示半字节。明文被分成了16个4 bit的明文组,用一个的矩阵表示：

1.1 符号说明

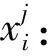
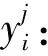
K(j,i):第j轮的轮密钥的第i个字节。

A:活跃字节,遍历多有可能值。

B:平衡字节,该字节和为0。

U:未知,字节性质不可知。

1.2 SubCell(s)

Midori64采用的S盒如表1所示。明文矩阵中每个单元需通过S盒。

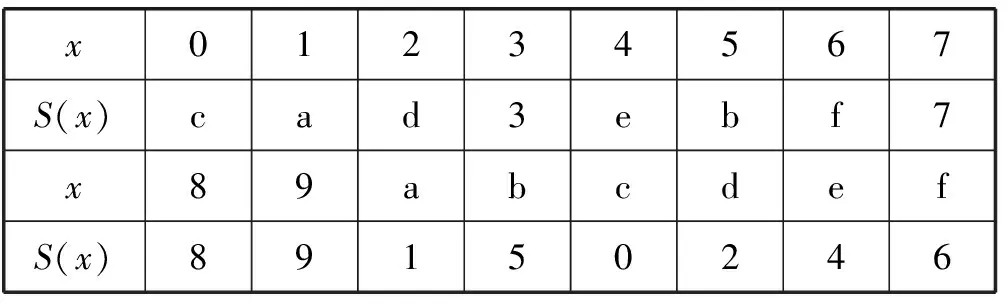
表1 Midori64的S盒

1.3 ShuffleCell(SC)

对明文矩阵中各个单元的进行位置重新排列,如下所示:

1.4 MixCloumn(MC)

用MDS矩阵M左乘ShuffleCell计算结果,执行列混淆变换,由于M具有自逆特性,其逆矩阵与其相同。

t(Si,Si+1,Si+2,Si+3)←M·t(Si,Si+1,Si+2,Si+3)

1.5 KeyAdd(AK)

将MixCloumn结果与轮密钥进行“异或”计算。

1.6 密钥编排

Midori的密钥编排将128 bit的主密钥取高64 bit记为K0,取低64 bit为K1,K=K0‖K1,定义白化密钥WK=K0⊕K1,轮密钥RKi=Ki mod2⊕ai(0≤i≤14)，ai为轮常量。

2 Midori64的积分区分器

2.1 Midori64的4轮积分区分器

命题1经过对Midori加密算法分析,选取输入的第一个字节为活跃字节,其余字节均为常数字节,则第4轮的输出中第一个字节为平衡字节。

证明: 设输入的第一个字节为活跃字节,其他字节均为常数字节,经过S盒以及SC后第一个字节仍为活跃字节,其余字节为常数字节,经过列混淆MC后,第一列的第2,3,4字节为活跃字节,其余字节为常数字节,接下来的密钥加AK操作不会改变字节性质。第二轮经过S盒后活跃字节位置不变,经过单元置换SC后,活跃字节的位置变为第8,10,15这三个字节,其余字节为常数字节,经过列混淆MC后,活跃字节位置为第5,6,7,9,11,12,13,14,16这9个字节。又由于密钥加AK操作不改变字节性质,因此第二轮输出后5,6,7,9,11,12,13,14,16这9个字节为活跃字节,其余为常数字节。第三轮经过S盒后活跃字节性质不变。经过单元置换SC后活跃字节位置为第2,3,4,6,7,11,12,14,16这9个字节,经过列混淆MC操作后字节性质发生改变,第1,2,3,4,5,8,9,13,15这9个字节为平衡字节,其余字节为活跃字节,最后AK操作不改变字节性质。这些字节在进入第四轮后,经过S盒后平衡字节性质发生破坏,变为未知状态,活跃字节性质不变。经过单元置换SC及列混淆MC操作后,第1个字节为平衡字节,其余字节均为未知状态,又由于密钥加AK操作不改变字节性质,因此第4轮的输出在进入第5轮后,平衡字节性质通过S盒发生破坏,即得到了Midori64的4轮积分区分器。如图1所示。

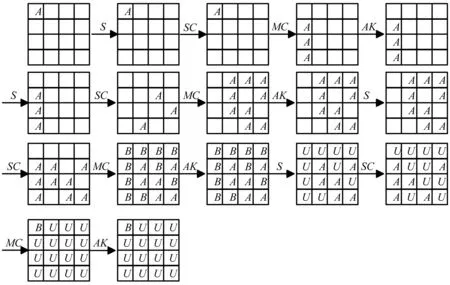
图1 Midori64的4轮积分区分器

2.2 Midori64的5轮积分区分器

由Midori的密码结构,可以将上述4轮积分区分器向前扩展一轮得到5轮高阶积分区分器。

命题2选取输入明文中4个字节(S0,S5,S10,S15)为活跃字节,其他字节为常数字节,则第5轮输出的首个字节为平衡字节。

证明:(S0,S5,S10,S15)这4个字节遍历所有216种取值,设输入的明文形式为:

(1)

式中：(A0,A5,A10,A15)为活跃字节,其余均为常数字节。经过一轮加密我们可以得到第一轮的输出为:

(2)

(3)

其余字节为常数字节,再利用4轮积分区分器经过4轮加密后第5轮输出的首字节为平衡字节。即得到Midori64的5轮积分区分器。如图2所示。

图2 Midori64的5轮积分区分器

3 Midori64的积分攻击

运用积分攻击的方法,我们对Midori64算法进行了6轮、7轮、8轮的攻击。

3.1 Midori64的6轮积分攻击

利用5轮区分器进行6轮攻击,过程如下:

(1) 选择如式(1)的一组明文,对其进行6轮加密,记密文为c0,c1,…,c216-1。

(2) 猜测第6轮首字节密钥K(6,0)的值,计算:

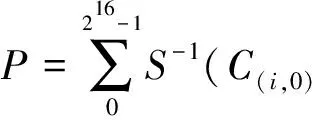
(4)

(3) 检验P=0是否成立,若成立,相应的K(6,0)作为一个正确密钥的候选值,否则淘汰。

(4) 重新选择一组明文,重复上述步骤,直到K(6,0)的值唯一确定。

复杂度计算如下:

若密钥K(6,0)为错误密钥,则错误密钥值使得P=0的概率为2-4,经过一组明文验证后,剩余的错误密钥个数为1-2-4<1,因此,需要两组明文就可以确定正确密钥。从而攻击的数据复杂度为2×216=217个选择明文。第一组明文需要进行216次6轮加密,需要进行24×24=28次S盒运算。一次6轮Midori64加密需要查询S盒96次,因此第一组明文需要进行(24×24)/96=21.41次6轮加密;处理完第一组明文后错误密钥最多还剩1个,因此对于第二组明文其共需要24次6轮加密,因此上述攻击的时间复杂度为216+21.41≈216次6轮加密运算。

3.2 Midori64的7轮攻击

在5轮区分器的后面加2轮可以进行7轮攻击。

将表3和5进行比较发现,各要素标注出的缺省指代数与各要素的缺省量不一致,那是因为缺省要素的标注只能根据篇章中已经存在的要素进行缺省要素补全,而一些事件的缺省要素在文中是没有描述的,这时是不能进行补全的,也就是说缺省指代只能根据已存在要素在一定程度上补全缺省要素.

(1) 选择包含216个不同明文组满足结构：

进行7轮加密。

经过AK、MC-1、SC-1、S-1操作后：

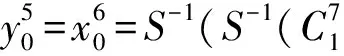
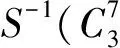
(5)

(6)

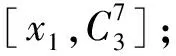
3.3 Midori64的8轮积分攻击

在上述7轮之后再加一轮,进行8轮攻击,根据加密算法结构得第5轮首字节输出与第6轮输出的表达式:

(7)

第6轮的输出第一列3个字节与第7轮输出的表达式:

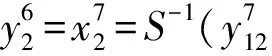
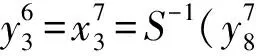
第7轮输出与第8轮密文的表达式:

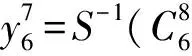
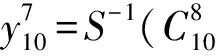
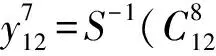
因此表达式为:

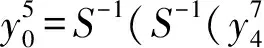
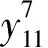
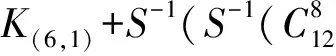
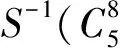
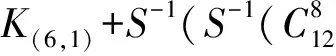
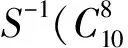
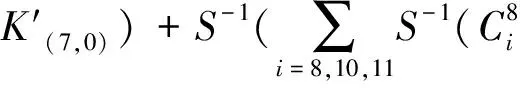
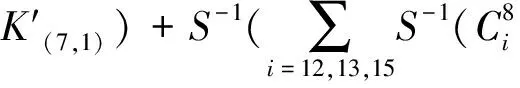
(8)

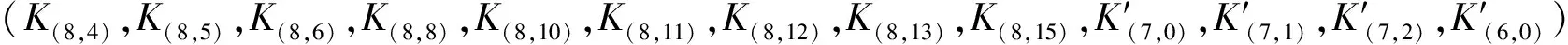
式中：

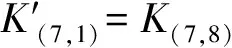
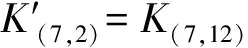
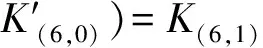
利用部分和技术优化其时间复杂度的计算,过程同上述7轮复杂度的计算过程,经过计算得到的数据复杂度为216×14=219.80个选择明文,时间复杂度为265次8轮加密。

3.4 3种积分攻击复杂度

整理文中对Midori64加密算法的6轮、7轮和8轮攻击的复杂度如表2所示。

表2 Midori64积分分析复杂度结果

4 结 语

本文对Midori64加密算法构造出了4轮积分区分器,并向解密方向扩展1轮,得到了5轮区分器。利用5轮区分器对Midori64进行了6轮、7轮和8轮的积分攻击。这是首次运用积分攻击来评估Midori64算法的安全性,从表2中可以看到,随着攻击轮数的增加,所需要恢复的密钥个数也在相应增加,在复杂度方面,6轮与7轮攻击的数据复杂度均为217个选择明文,但在时间复杂度上面,7轮大于6轮。8轮攻击一共需要恢复52 bit密钥,数据复杂度为3×216个选择明文,时间复杂度为258.43次8轮加密,相比于穷举搜索复杂度有所增加。

通过猜测相关轮密钥与密文的关系,可以进一步学习到积分攻击过程中平衡字节与密文的对应关系,进而得到每一轮中所用到的相关字节密钥,进而可以采用部分和技术来降低恢复密钥的时间复杂度。