多楔带传动系统特征值灵敏度分析*

李传兵，伍 村，胡玉梅，，彭 红，刘 进

(1.汽车噪声振动和安全技术国家重点实验室，重庆 400039;2.重庆大学，机械传动国家重点实验室，重庆 400044)

前言

单根多楔带传动广泛应用于发动机的前端轮系中，用来驱动发电机、空调和转向助力泵等附属设备。这个系统的一个主要特点是引入了一个自动张紧器，能自动补偿张力的损失，使带段中的张力保持稳定，以提高系统的动态性能。

单根多楔带传动系统在过去20年中被广泛应用，对其振动的研究很多，大多只考虑带轮的旋转振动［1-3］，采用比较简单的离散模型。但也有学者开始采用更精确的模型，除带轮旋转振动外，还研究带的横向振动和连续带与离散轮之间的耦合振动［4-6］。以上模型都把带简化为弦，但近年来，已有人将带简化为纵向运动的伯努利-欧拉梁，建立了轮-带梁耦合振动模型［7-8］。

在特征值灵敏度方面，文献［9］中基于文献［4］建立的模型与求解方法，推导了便于直接求解的系统固有频率对于张紧机构各设计参数的灵敏度控制方程。文献［10］中推导了一个N轮多楔带传动系统的特征值灵敏度的通用表达式，然后在坐标转化中加入路径搜索以提高搜索效率，并以带段横向位移和带轮振动角位移最小为目标函数进行系统的优化。结果表明，优化后系统振动明显减小。文献［11］中基于文献［5］建立的模型与求解方法，推导了多楔带传动系统的频率对系统结构参数灵敏度的显式表达式。以上的特征值灵敏度分析仅限于轮-带弦耦合模型，但弦耦合模型(不能考虑带的弯曲刚度)不能很好地描述多楔带传动系统的振动问题［8］，使灵敏度分析也有其局限性。本文中基于轮-带梁耦合振动模型［7-8］，利用结构振动分析的矩阵摄动理论，推导了系统的固有频率对系统设计参数灵敏度的显式表达式，并应用到文献［8］的三轮系统中，计算了其1阶固有频率随系统结构参数的变化。本文中的灵敏度分析可以揭示系统的设计参数对系统振动频率的影响，对解决相关振动和噪声问题具有很好的指导意义。

1 系统振动模型的建立

一个典型的三轮多楔带传动模型如图1所示，此模型包含驱动轮1、张紧轮2、从动轮3、张紧臂4和单根多楔带等元件。图中:ui和wi(i=1，2，3)分别为带段的纵向位移和横向位移，均为时间t和位置xi的函数，xi为带张紧时各带段起点至终点的位置坐标，其范围(0，li);li，θi，Ji和 ri分别为带段的长度、带轮的旋转角位移、转动惯量和半径;rt，Jt，θt和Kt分别为张紧臂的臂长、绕固定点的转动惯量、旋转角位移和张紧器弹簧的扭转刚度;c为带的纵向速度;表示带段下标i的设定:1为轮1与轮2之间的带段;2为轮2与轮3之间的带段;3为轮3与轮1之间的带段。带段1和带段2与张紧臂的夹角分别为 β1和 β2。

本文中将带段看作是纵向运动的伯努利-欧拉梁，假设带以准静态方式伸缩;带段物理性质各向一致;轮-带间无滑动，各带轮和张紧臂均看成是刚体。依据以上的假设，应用Hamilton原理和牛顿第二定律，对带段和各旋转件建立系统的运动方程［8］。

各带段的运动方程为

式中:m为带的线密度;EI为带的弯曲刚度;Pi和˜Pi分别为带段的稳态张力和动态张力。

各带轮的运动方程为

再利用伽辽金法［8］将带的横向位移分离为时间函数和空间函数乘积求和形式，选择的空间基函数为正弦函数。Ni表示带段i所选基函数的数目，本文取Ni=6，则各带段横向位移可表示为

为了后面灵敏度表达式的简洁，设

将式(7)代入式(1)～式(5)系统方程中并写成矩阵形式:

对式(9)矩阵方程应用复模态理论可求解系统的固有特性和位移响应。

2 特征值灵敏度分析

本文中在灵敏度表达式推导中考虑带速为0的情况，而带速不为0的情况其方法也相同。当系统某设计参数κ发生小变化时，可通过质量矩阵和刚度矩阵的改变反映出来。假设参数κ发生改变后的质量矩阵和刚度矩阵为

式中:ε为一个小参数;M0和K0分别为原系统的质量矩阵和刚度矩阵;εM1和εK1分别为参数κ发生小变化引起的质量矩阵和刚度矩阵的变化。根据文献［12］可得到系统特征值1阶摄动如下:

式中:εK1/Δκ和εM1/Δκ可表示为刚度矩阵和质量矩阵对参数 κ 求偏导，即 ∂K/∂κ 和 ∂M/∂κ，因此特征灵敏度可表示为

式中:K'表示刚度矩阵对参数κ求偏导;M'表示质量矩阵对参数 κ 求偏导，即 ∂K/∂κ 和 ∂M/∂κ。其中κ是具体的结构参数和力学参数，即本文中张紧臂的转动惯量、扭转刚度和张紧臂的长度等参数。

根据式(12)就可方便地求出系统第i阶固有频率对某参数κ的灵敏度。下面将给出系统第i阶固有频率对具体结构参数的灵敏度显式表达式。

观察刚度矩阵和质量矩阵，可发现张紧器无量纲刚度ks仅与刚度矩阵有关。系统第i阶固有频率对张紧器刚度ks的灵敏度μ|ks可表示为

系统第i阶固有频率对张紧臂长度rt的灵敏度计算公式为

3 算例

3.1 固有特性计算

本文中系统振动模型的建立采用文献［8］的方法，在正确模型的基础上导出了式(13)～式(15)特征值灵敏度的显式表达式。为了验证本文对文献［8］中模型数值计算的正确性，对该三轮模型的固有频率进行了计算和对比。三轮系统的参数［8］见表1。

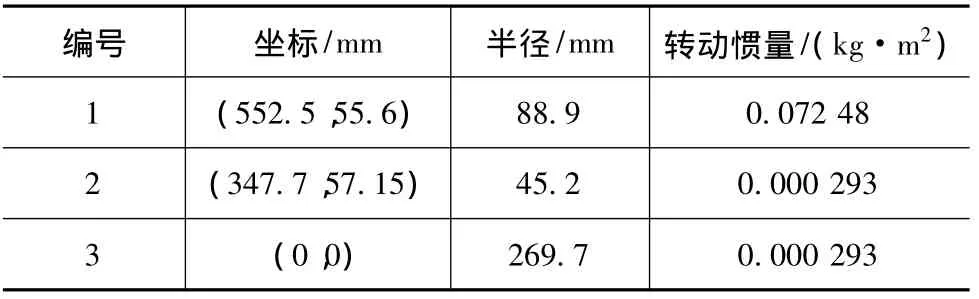
表1 3个带轮相关参数

图2是本文中计算的各阶固有频率随带的弯曲刚度的变化曲线与文献［8］中曲线的对比。由图可见，它们吻合良好，说明本文对文献［8］中模型数值计算的正确性。

表2是带的无量纲弯曲刚度为0.05时系统前6阶的固有频率，图3是系统前4阶的阵型。从图3中可以看出带的横向振动与带轮的旋转振动始终是耦合的，这与实际发动机轮系的振动是吻合的［8］。而弦耦合模型，则存在横向振动占优、旋转振动占优和耦合振动3种类型模态［6］，耦合振动耦合度不高。因此，梁耦合模型相对于弦耦合模型更能揭示发动机实际的振动情况。

表2 系统的前6阶固有频率

3.2 稳态响应对灵敏度计算的影响

本文中在推导式(13)～式(15)时忽略了稳态响应的影响，一方面是因为稳态响应随参数的变化值不大，另一方面是因为推导时稳定状态的响应无法用显式表达式表达。这是因为稳态响应方程［7］包含微分方程、代数方程和积分方程，难以与动态响应的线性矩阵方程［8］直接组合在一起，只能把稳态过程当成一个常量，对动态过程进行特征灵敏度分析。

为了说明稳态响应对本文中计算的灵敏度影响不大，在此计算了带段1和带段3的稳态响应随张紧器弹簧扭转刚度Kr、张紧臂的转动惯量Jt和张紧臂长度rt的变化曲线，如图4～图6和表3所示。

图4～图6和表3均说明，稳态响应随各参数的变化值确实不大，推导时忽略了稳态响应的影响是合理的。

3.3 灵敏度计算

系统的低阶频率通常是关注的重点，因此本文中将通过计算第1阶固有频率对张紧器弹簧扭转刚度Kr、张紧臂的转动惯量Jt和张紧臂长度rt等的灵敏度，从而总结第1阶固有频率随这些参数的变化规律。同时，为了验证推导的灵敏度公式的正确性，对计算的1阶固有频率随系统结构参数的变化曲线通过差分方法［10］得到系统的灵敏度曲线与本文中推导的式(13)～式(15)灵敏度显式表达式得到的曲线进行了对比，如图7～图9所示。

表3 各参数对带段1、3稳态响应的影响

由图7可见，第1阶固有频率对张紧器扭转刚度的灵敏度始终为正数，说明固有频率始终随张紧器扭转刚度的增大而增大，这与图中带“o”的曲线所表达的趋势一致;固有频率对于张紧器扭转刚度的灵敏度随张紧器刚度的增大而减小，说明固有频率随张紧器刚度的增大而增大的趋势在逐渐减小。

由图8可见:灵敏度始终为负值，与图中第1阶固有频率逐渐下降对应，且下降的变化率是一条类似二次开口向上的抛物线。

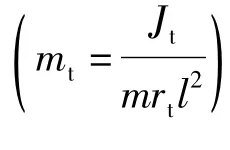
从图7～图9中差分法得到的灵敏度曲线与灵敏度显式表达式得到的灵敏度曲线不重合与各参数对稳态响应的影响分析对比可发现，本文中推导的灵敏度公式有误差是由于忽略稳态响应引起的(主要在图9中)，且误差的大小与此参数对稳态响应的影响大小呈正比，这从对比图7～图9中的曲线与表3中的数据可看出。

4 结论

(1)建立了轮-带梁耦合振动模型，通过摄动分析，给出了用设计参数计算固有频率的通用表达式，然后推导了系统固有频率对系统设计参数灵敏度的显式表达式。

(2)计算了梁模型前4阶的固有模态，计算结果表明梁模型中带的横向振动和轮的旋转振动始终是耦合的，而弦模型中仅与张紧轮相邻的带段与轮是耦合的，因此两模型的振动形式是不同的。

(3)通过灵敏度曲线分析了固有频率随某些设计参数而变化的规律，并通过各参数对系统稳态响应的分析，解释了本文中推导的灵敏度表达式存在误差的原因。

［1］ Hawker L E.A Vibration Analysis of Automotive Serpentine Accessory Drives Systems［D］.Ontario:University of Windsor，1991.

［2］ Barker C R，Oliver L R ，Breig W F.Dynamic Analysis of Belt Drive Tension Forces During Rapid Engine Acceleration［C］.SAE Paper 910687.

［3］ Hwang S J，Perkins N C，Ulsoy A G，et al.Rotational Response and Slip Prediction of Serpentine Belt Drives Systems［J］.Journal of Vibration and Acoustics，1994，17:71-78.

［4］ Beikmann R S，Perkins N C，Ulsoy A G.Free Vibration of Serpentine Belt Drive Systems［J］.Journal of Vibration and Acoustics，1996，118:406-413.

［5］ Zhang L，Zu J W.Modal Analysis of Serpentine Belt Drive Systems［J］.Journal of Sound and Vibration，1999，222(2):257-279.

［6］ Parker R G.Efficient Eigensolution，Dynamic Response and Eigensensitivity of Serpentine Belt Drives［J］.Journal of Sound and Vibration，2004，270(1):15-38.

［7］ Kong L Y，Parker R G.Equilibrium and Belt-pulley Vibration Coupling in Serpentine Belt Drives［J］.Journal of Applied Mechanics，2003，70(5):739-750.

［8］ Kong L Y，Parker R G.Coupled Belt-pulley Vibration in Serpentine Belt Drives with Belt Bending Stiffness［J］.Journal of Applied Mechanics，2004，71(1):109-119.

［9］ 劳耀新，侯之超，吕振华.发动机前端附件带传动系统频率灵敏度分析［J］.汽车工程，2006，28(5):477-481.

［10］ Hou Zhichao，Lao Yaoxin，Lu Qiuhai.Sensitivity Analysis and Parameteroptimization forVibration Reduction ofUndamped Multi-ribbed Belt Drive Systems［J］.Journal of Sound and Vibration，2008，317:591-607.

［11］ 侯之超，王象武，劳耀新.多楔带传动系统的频率灵敏度分析［J］.机械工程学报，2009，45(11):250-255.

［12］ 陈塑寰.结构振动分析的矩阵摄动理论［M］.重庆:重庆出版社，1991.