提高制动尖叫复模态有限元模型预测精度的方法*

刁 坤，张立军，孟德建，余卓平

(1.同济大学汽车学院，上海 201804;2.新能源汽车工程中心，上海 201804)

前言

制动摩擦尖叫的发生机理复杂，影响因素众多，目前尚未取得统一认识，亦未建立完全有效的控制措施［1］。作为一种重要的数值计算手段，有限元法在制动尖叫发生机理研究、影响因素分析和结构设计方面发挥重要作用［2］。其中，随着ABAQUS等商业化软件的广泛应用，最早在文献［3］中提出的有限单元复模态分析法日益成为行业内比较流行的制动尖叫预测方法［2］。所谓复模态分析，就是基于模态耦合理论，考虑制动盘和制动块之间的摩擦耦合作用导致的系统刚度矩阵的不对称性，分析正实部特征值对应的不稳定模态，即制动尖叫模态的方法［3］。近年来，随着应用的不断深入，制动器各部件特性对复模态的影响，以及复模态的预测精度和可靠性问题［1-4］日益受到重视。

在为分析复模态有限元模型的有效性和正确性而对不稳定频率的计算结果与尖叫试验结果进行对比时，人们常发现:计算得到的制动尖叫频率数量与实际尖叫的频率数量不符，存在明显的“过(多)预测”和“欠(少)预测”问题。为了提高复模态模型的精度，在复模态建模时都会针对制动器各部件进行基于模态试验的模型验证，确保各部件结构特性模型的正确性［3-15］。同时，很多研究中开始考虑制动盘/摩擦材料弹性模量［5，8］、各部件阻尼特性［6］、制动块开槽与倒角［5，7］、消音片［8］、制动盘形状与尺寸［9］、摩擦衬片材料的各向异性［10］、摩擦因数的时变性［8，11］、形貌与接触特性［11-13］和摩擦热机耦合［8，12，14-15］的影响。但是，预测精度问题仍然没有得到根本的解决。笔者综合分析认为，复模态理论的稳态线性化假设、前期分析中忽略了制动器各部件复杂的接触连接关系和制动尖叫的不确定性可能是影响预测精度的主要因素。

在此背景下，本文中针对某通风盘式制动器，考虑制动尖叫的随机性，从统计分析的角度进行3个同型号制动器的多工况制动尖叫试验和尖叫频率综合统计分析;然后建立制动器尖叫复模态分析的原始模型和改进模型，进行复模态不稳定频率的预测和与结合试验结果的对比，分析制动器导向销等零件和各个部件间的摩擦接触关系对复模态频率预测精度的影响。由此，建立了一种通过制动尖叫统计性试验，建立考虑各部件接触和连接关系的复模态模型的方法，为提高复模态有限元模型的预测精度和分析可靠性提供重要依据。

1 制动尖叫台架试验和分析

当试验次数较少时，可能发生尖叫“频率丢失”现象，也会在复模态计算结果与试验结果对比时加剧频率的“过预测”的现象。因此，本文中借鉴多套制动器、多工况和多次试验的方法［16］，进行3套相同制动器多工况下的尖叫台架试验，对尖叫频率和声压级进行统计分析。

1.1 测试传感器的设置

制动尖叫台架试验在多功能惯量式制动器动力学试验台上进行。根据研究需求，在试验中设置了传声器和振动加速度、盘面端面跳动位移、制动转矩、制动盘转速与制动油压等传感器。其中，与本文紧密相关的传声器、加速度传感器和端面跳动传感器的布置情况如下。

(1)传声器 传声器用于测量制动尖叫，其布置位置要求如下:a.安装在距离轮毂面外侧沿车轴中心线10cm处;b.安装在距离垂直于车轴中心线50cm处，如图1所示。

(2)振动加速度传感器 采用压电式三向振动加速度传感器，如图2所示，分别布置在制动器的制动钳(测点1)、保持架(测点2)和外侧制动背板(测点3)上。

(3)位移加速度传感器 在制动盘的内侧、制动块的对侧布置一个位移传感器，位置在摩擦衬片等效作用半径115mm处，与摩擦衬片对称线夹角为180°，如图3 所示。

1.2 试验工况的设置

为了确保试验的可靠性和数据的准确性，试验设置参考SAE J2521—2006标准，环境温度为室温，环境湿度控制在20% ～90%内，环境噪声不高于60dB。选取3套同型号的制动器，进行多种工况的多次组合试验:不同制动压力(0.4～4.5MPa)、不同转速(50～500r/min)、不同初始制动温度(25～150℃)下，分别采用减速制动和拖曳制动各进行50次试验。详细信息参见文献［14］。

1.3 试验频率统计分析

参考SAE J2521—2006标准，不包括悬架的制动器总成的尖叫频率应在2～17kHz范围内，且尖叫声压级应大于70dB。由于试验时未能采用非接触式测量装置测量尖叫时制动器的变形，本文只参照SAE J2521—2006标准提取制动尖叫频率进行分析，得到如图4所示的3套制动器的制动尖叫频率。由图4可见，制动尖叫具有明显的随机性特性，具体表现如下。

(1)每套制动器的尖叫频率和声压级既有相同点，又有不同点，表现出一定的离散度。这可能是由于每套制动器在台架上进行安装时，各部件之间的具体连接关系(如导向销处回位装置等)和制动盘的端面跳动等存在差异所致。

(2)一套制动器在不同工况下的尖叫特性也不尽相同，这是因为不同的工况下的摩擦接触条件、热机耦合和系统的受力状态不同。

(3)每个制动尖叫频率也具有一定的分散性，通常分布在其中心频率±150Hz的范围内(详见图4局部放大图)。而且，不同尖叫频率在3套制动器的试验中出现的次数也不一致(见表1)。

表1 3套制动器的制动尖叫台架试验统计结果

2 制动尖叫复模态有限元模型

本文中基于ABAQUS有限元分析软件，建立制动尖叫复模态模型，实现各部件建模与接触连接定义，以及对应试验工况的制动盘旋转和制动压力等工况的设置。

2.1 制动器有限元模型

本文中所研究的通风盘式制动器系统包括制动盘、内/外摩擦衬片、内/外制动背板、制动钳、保持架、活塞、导向销和橡胶密封圈等共10个部件。建模时，在对制动器的CATIA模型进行必要的几何清理后，利用 Hyperworks软件进行网格划分，得到如图5所示的制动器系统有限元模型。其中，制动钳由于结构不规则，主要采用了四面体单元(C3D4);其余零件采用六面体单元(C3D8)为主，复杂的局部结构以五面体单元(C3D6)为辅的方式进行网格划分。制动器系统模型总单元数为107 781个。

2.2 各零件材料属性的定义

通过对比部件的自由模态计算结果与测试结果，不断修正得到各个部件的材料属性，包括密度、弹性模量和泊松比等参数，确保各个零件的自由模态仿真结果与试验结果的频率误差控制在5%以内，保证系统模型各零部件的结构和材料属性具有足够的精度。各个部件的具体参数如表2所示，表3则示例性地列出了制动盘的前5阶模态频率计算与测试结果对比以及模态振型的情况。限于篇幅，其他详细信息参见文献［14］。

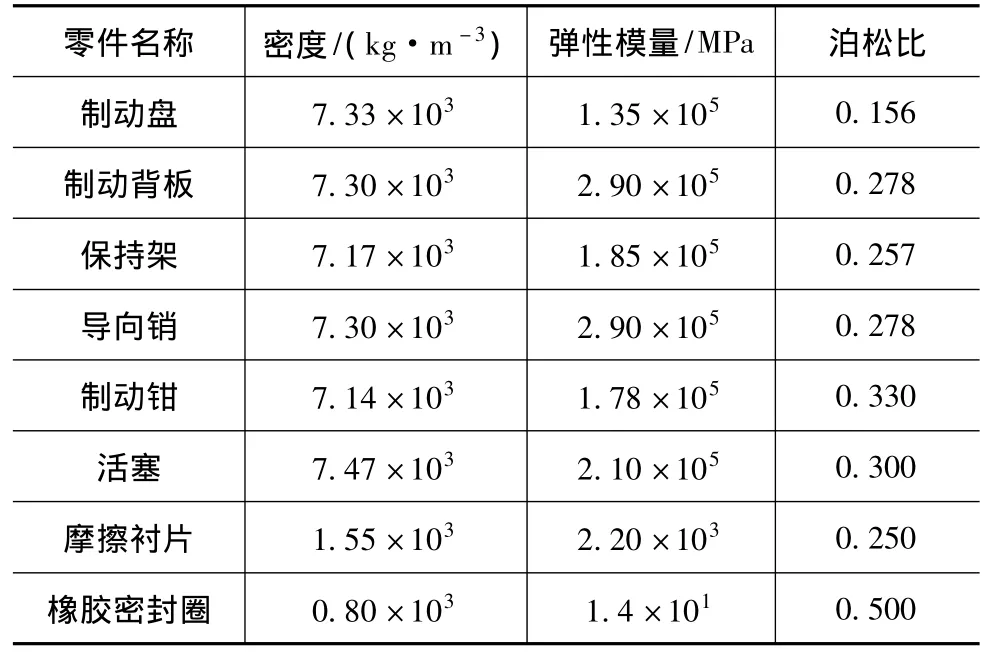
表2 各零件材料属性

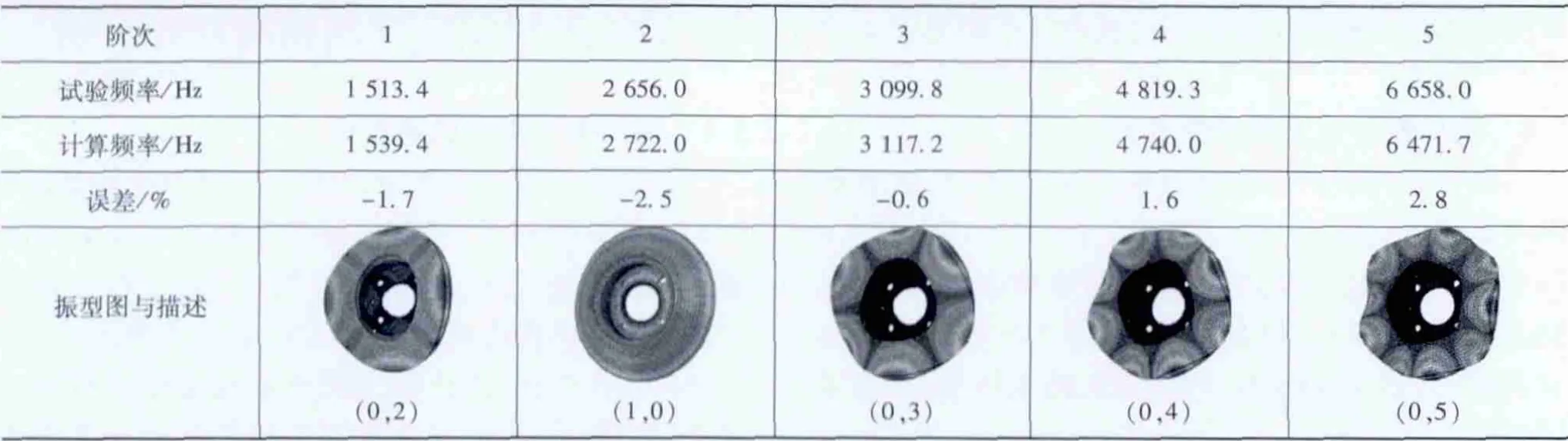
表3 制动盘模态计算结果与试验结果对比

2.3 各零件连接关系的定义

在保证制动器各部件的结构尺寸和材料属性具有较高精度的基础上，文献［14］参考文献［13］建立了盘式制动器复模态分析模型(以下简称为“原始模型”)，成功实现了制动尖叫的预测，但是存在明显的“过预测”和“欠预测”问题。分析发现，模型中各个零件之间的接触连接关系定义对制动尖叫的预测具有重要的影响。因此，本文中采用“Tie”、“Surfto-Surf Contact”和“Spring”等方式，结合实际制动器的结构和工作原理，对各个部件间的接触连接关系进行更准确的定义，建立了改进的制动器复模态分析模型(以下简称为改进模型)。两种模型具体设置说明和对比情况如表4所示。需要说明的是，制动盘与摩擦衬片之间的摩擦因数μ定义为0.3至0.6间隔0.1依次定义［17］，而其他的主摩擦副的摩擦因数参照摩擦副材料查阅机械设计手册等定义为0.2［18］。

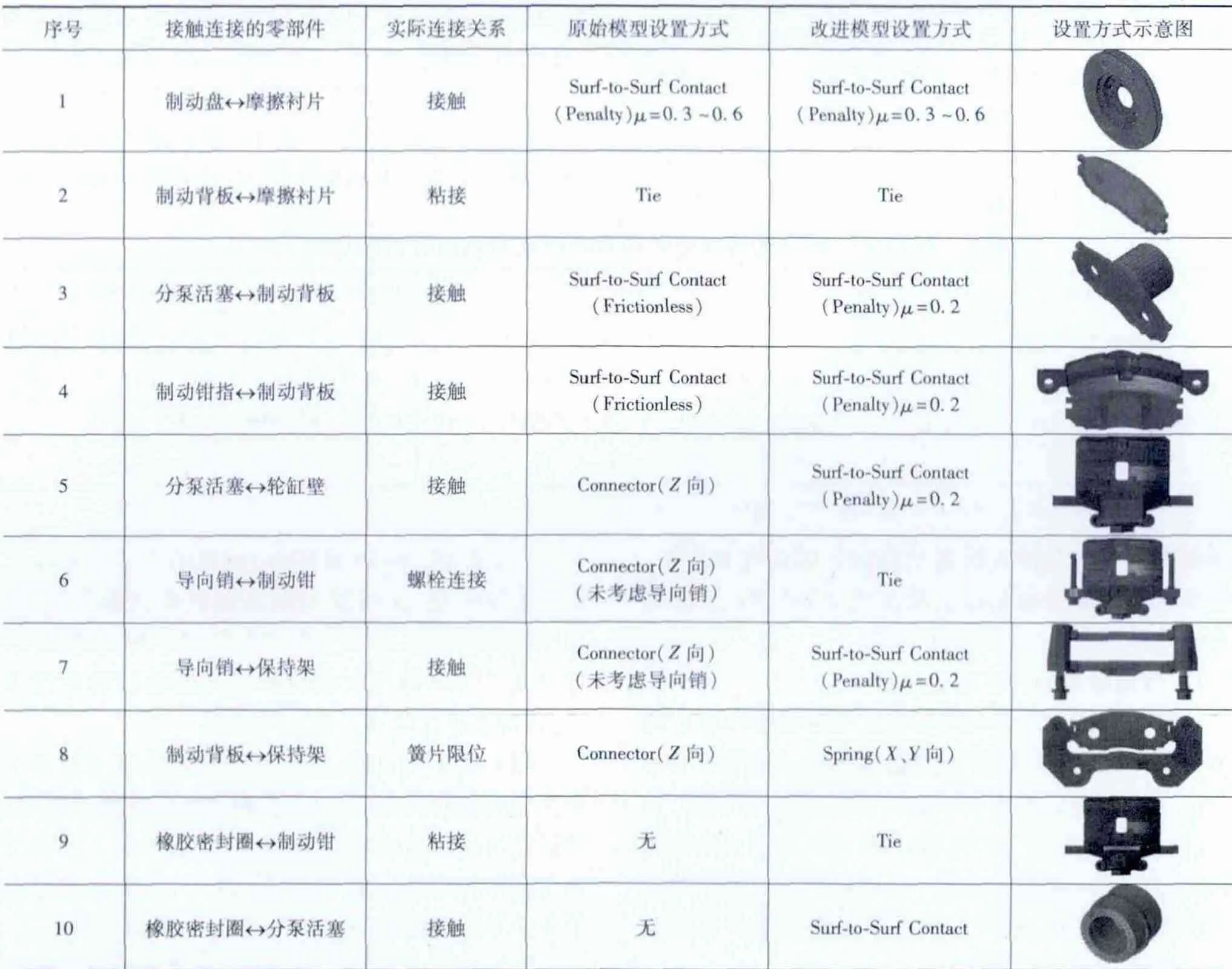
表4 制动器复模态原始模型与改进模型各零部件的连接关系设置和对比

2.4 边界条件定义和载荷设置

保持架与转向节柱通过螺栓紧固连接，故限制保持架螺栓孔的3个平动和3个转动自由度，如图6(a)所示;制动盘帽部通过螺栓与轮毂连接，仅可以绕Z轴转动，故约束制动盘帽部螺栓孔的3个平动自由度，并在Keywords里定义其转动效应，如图6(b)所示。

制动时制动分泵轮缸里充满制动液，各方向压力相等。因此，载荷设置时在活塞底面施加制动压力，而在对面施加同等大小的等效集中力，大小根据实际制动尖叫台架试验的制动压力和几何尺寸设定。

3 制动尖叫频率预测精度对比分析

3.1 制动尖叫预测结果对比

分别基于原始模型和改进模型，在摩擦因数μ=0.3～0.6的条件下，参照试验工况进行制动尖叫的复模态计算和分析。将计算得到的不稳定模态频率与试验得到的模态频率进行对比，如表5所示。

由表5可知，改进模型能更有效和准确地预测制动尖叫频率，说明各个部件连接关系的改进能够显著提高预测精度。具体分析如下。

(1)原始模型的预测结果存在严重的“欠预测”，出现了 5个“欠预测”频率(2.311、3.200、4.510、9.008和1.009 5kHz);而改进模型只存在1个“欠预测”频率(3.200kHz)。可见，改进模型很大程度上解决了制动尖叫的“欠预测”问题，尤其是在中低频段。

(2)原始模型的预测结果出现了2个“过预测”频率(7.913和14.450kHz);而改进模型只有1个“过预测”频率(8.195kHz)，有效改善了制动尖叫“过预测”问题。

(3)两种模型都“欠预测”的3.200kHz频率和预测误差相对较大的5.508kHz频率，都只在第一套制动器的尖叫台架试验中出现，这可能与第一套制动器安装时具有较大的制动盘初始端面跳动有关。模型建立时未考虑制动盘端面跳动的影响，因此出现频率预测不一致和较大的误差。

表5 制动尖叫频率复模态分析结果与制动尖叫台架试验结果的对比

3.2 模型改进的内在原因分析

下面根据预测得到的不稳定尖叫频率和模态振型，分析改进模型提高预测精度的根本原因。表6为改进模型预测得到的不稳定模态频率和振型，其中，振型取Z方向上的位移分布，同时显示从活塞侧和钳指侧进行观察的结果。通过对不同频率下的部件模态耦合关系，分析总结各个部件连接关系的改进对模型预测精度的影响。

(1)2.382和13.494kHz频率的不稳定模态主要是由导向销、保持架和制动盘的模态耦合引起。与原始模型相比，改进模型增加考虑了导向销部件，并定义了导向销与制动钳和保持架的接触连接关系，从而准确预测出了该尖叫频率。

(2)在4～11kHz频率范围内的不稳定频率主要由制动盘和活塞侧、钳指侧制动块模态耦合而成。改进模型在原始模型的基础上，增加考虑了制动背板与活塞和钳指接触界面的摩擦力，从而多预测出了3个不稳定模态(4.666、9.202和10.074kHz)。

(3)在高于11kHz频率的大多数不稳定模态由单个零件的高频局部模态与制动盘耦合而成，改进模型考虑的多个相关部件的接触连接关系产生综合效应，有效解决了尖叫频率(14.450kHz)的“过预测”问题。

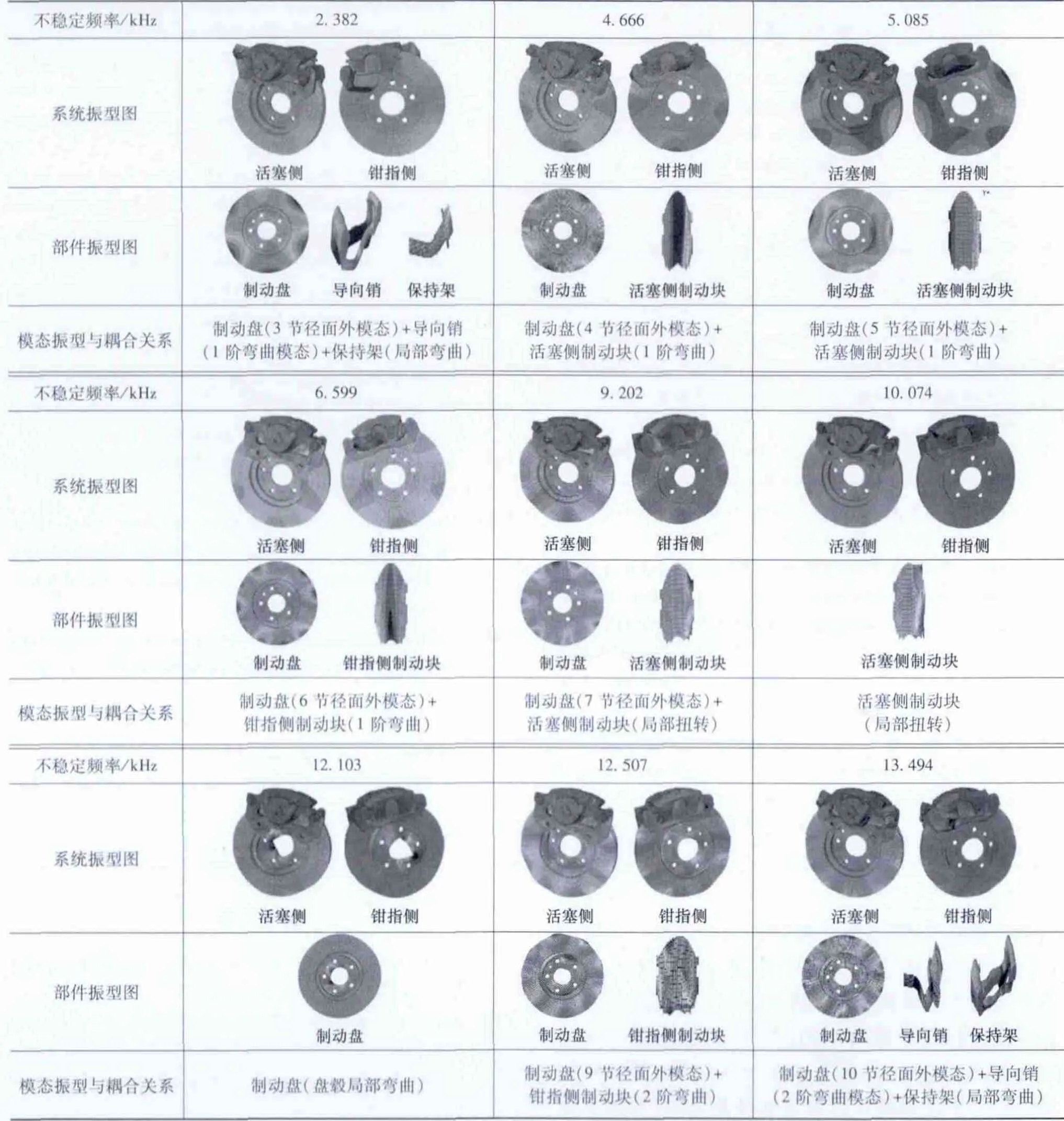
表6 改进模型的不稳定模态频率和振型

4 结论

(1)准确有效的制动尖叫台架试验是制动尖叫复模态有限元模型验证和评价的基础。考虑制动尖叫的“不确定性”，从统计分析的角度出发，对多套相同型号的制动器进行多工况多次试验，对尖叫频率和声压级进行统计分析，可以有效地解决制动尖叫台架试验的“丢频率”问题。

(2)通过详细考虑导向销等容易被忽略的部件和考虑非主摩擦副之间的接触摩擦作用等，不仅可以有效提高尖叫频率的预测精度，还可以有效解决“欠预测”和“过预测”问题。

(3)但本文研究中的“欠预测”和“过预测”问题尚未能完全消除，还须进行深化研究。

［1］ Carlo C，Riccardo C，Giampiero M，et al.Brake Comfort-a Review［J］.Vehicle System Dynamics，2009，47(8):901-947.

［2］ Ioannidis P，Brooksand P C，Barton D C.Brake System Noise and Vibration-a Review［C］.Proceedings of Braking 2002.From the Driver to the Road.Papers from the International Conference，Leeds，United Kingdom，2002.

［3］ Liles G D.Analysis of Disc Brake Squeal Using Finite Element Methods［C］.SAE Paper 891150.

［4］ Liu E C，Kung S W，Jenq S T，et al.Effect of Chamfered Brake Pad Patterns on the Vibration Squeal Response of Disc Brake System［C］.3rd International Symposium on Advanced Fluid/Solid Science and Technology in Experimental Mechanics.Tainan，Taiwan，2008.

［5］ Nouby M，Mathivanan D，Srinivasan K.A Combined Approach of Complex Eigenvalue Analysis and Design of Experiments(DOE)to Study Disc Brake Squeal［J］.International Journal of Engineering Science and Technology，2009，1(1):254-271.

［6］ Fritz G，Sinou J J，Duffal J M，et al.Effects of Damping on Brake Squeal Coalescence Patterns-application on a Finite Element Model［J］.Mechanics Research Communications，2007(34):181-190.

［7］ Oberst S，Lai J C S.Numerical Prediction of Brake Squeal Propensity Using Acoustic Power Calculation［C］.Proceedings of ACOUSTICS 2009，Adelaide，Australia，2009.

［8］ Ma'rio Triche^s Ju'nior，Samir N Y Gerges，Roberto Jordan.Analysis of Brake Squeal Noise Using the Finite Element Method:A Parametric Study［J］.Applied Acoustics，2008(69):147-162.

［9］ Saw Chun Lin，Abd Rahim Abu Bakar，Wan Mohd Musyris WanHarujan.Suppressing Disc Brake Squeal Through Structural Modifications［J］.Jurnal Mekanikal，2009(29):67-83.

［10］ Oberst S，Lai J C S.Numerical Study of Friction-induced Padmode Instability in Disc Brake Squeal［C］.Proceedings of 20th International Congress on Acoustics，ICA 2010，Sydney，Australia，2010.

［11］ Dai Y，Lim T C.Suppression of Brake Squeal Noise Applying Finite Element Brake and Pad Model Enhanced by Spectral-based Assurance Criteria［J］.Applied Acoustics，2008(69):196-214.

［12］ Abd Rahim Abu Bakar，Mohd Kameil Abdul Hamid，Afandi Dzakaria，et al.Stability Analysis of Disc Brake Squeal Considering Temperature Effect［J］.Jurnal Mekanikal，2006(22):26-38.

［13］ AbuBakar A R，Ouyang H J，James S，et al.Finite Element A-nalysis of Wear and Its Effect on Squeal［J］.Proceedings of the Institution of Mechanical Engineers，Part D:Journal of Automobile Engineering，2008，222(7):1153-1165.

［14］ 唐扬扬.热机耦合效应对盘式制动器尖叫的影响分析［D］.上海:同济大学，2011.

［15］ Hassan M Z，Brooks P C，Barton D C.A Predictive Tool to Evaluate Disk Brake Squeal Using a Fully Coupled Thermo-mechanical Finite Element Model［J］.International Journal of Vehicle Design，2009，51(1-2):124-142.

［16］ Butlin T，Woodhouse J.A Systematic Experimental Study of Squeal Initiation［J］.Journal of Sound and Vibration，2011，330:5077-5095.

［17］ 张立军，缪唯佳，余卓平.汽车盘式制动器摩擦-振动耦合特性试验研究［J］.摩擦学学报，2008，28(5):480-484.

［18］ 王文斌，等.机械设计手册［M］.北京:机械工业出版社，2008.