混合贝塔分布随机波动模型及其贝叶斯分析

白仲林，隋雯霞，刘传文

（1．天津财经大学 理工学院，天津 300222；2．天津市发展和改革委员会，天津 300040）

一、引 言

1986年Taylor提出利用离散时间随机波动模型（简称SV模型）刻画金融资产收益率的波动问题以来，SV模型在金融市场分析中得到了广泛应用，但是随机波动模型的基本假设往往与现实不一致。于是，学者们分别从金融资产收益率的高峰厚尾性、非对称性和长记忆性等方面对基本SV模型进行了扩展。例如Jacquier和Nicholas等假设资产收益率服从t分布，提出了SV－t模型，它较好地反映了收益率的厚尾特征［1］；Cappucci和Lubian基于厚尾的广义误差分布提出了偏GED随机波动模型，该模型不仅反映了资产收益率的厚尾性，而且能够刻画资产收益率分布的非对称性［2］；Bovas和Ranjini还提出了一种伽马随机波动（SV－Γ）模型，它较好地刻画了资产收益率的尖峰厚尾性［3］；Mike等提出了门限随机波动（THSV）模型，它不仅刻画了波动率的非对称性，而且还考虑了均值本身的非对称性［4］；Bredit等提出长记忆随机波动模型（SVLM），提供了一种分析高频收益率波动性的方法［5］；Luis等人在SV－LM中引入内生的结构突变点，进而分析了突变点对长记忆性模型的影响［6］。另外，邱崇洋、刘继春和陈永娟将一阶自回归的SV模型扩展为一般的形式，即波动率方程是对数ARMA（1，1）过程的SV 模型［7］；周宏山、冀云利用非对称随机波动模型对中国股市进行实证分析，发现非对称随机波动模型能够较好地探测到波动存在的非对称波动［8］；郝立亚、朱慧明等通过对模型在状态空间框架下的近似表示，将向前滤波、向后抽样算法引入对波动变量的估计过程中，设计出Gibbs联合抽样算法，提高了长记忆随机波动模型的贝叶斯抽样效率［9］。从上述列举可见，目前SV模型及其扩展模型的研究重点在于对金融资产收益率的尖峰厚尾性、非对称性和长记忆性等的刻画。金融市场的一些特殊交易规则对收益率的分布也存在严重影响，例如涨跌停板制度使收益率分布具有有限区间取值特征，制约了传统SV建模方法的应用。

为了在中国股票市场的特殊交易规则（日交易的10%涨跌停板制度）下分析股票收益率的分布，本文首先从中国股票市场交易规则出发选择混合贝塔分布来刻画资产收益率的分布，建立基于混合贝塔分布的SV模型，并讨论了混合贝塔分布随机波动模型的贝叶斯估计方法。最后以上证A股综合指数简单收益率为例，分别建立基于混合贝塔分布和正态分布的SV模型，比较研究发现基于混合贝塔分布的SV模型能够更全面地刻画市场收益率的时变特征，较准确地描述金融资产收益率数据的真实数据生成过程。

二、混合贝塔分布及其特征

为了反映金融资产收益率分布的尖峰厚尾性、非对称性和有限区间取值等特征，本文借鉴混合正态分布的构造方法，采用混合贝塔分布拟合收益率分布。

贝塔分布是一类取值于有限区间的分布，如果随机变量X服从标准贝塔分布，则X的密度函数为：

其中a、b均大于0，记X～beta（a，b）。

设pk为随机变量X来自第k类贝塔分布的概率，且∑pk＝1，则称密度函数为：

它的随机变量X服从混合贝塔分布，其中fk（x）为第k类贝塔分布的密度函数，其公式为：

k＝1，2，…，K

本文中设定随机变量X服从K＝2的混合贝塔分布，记服从混合贝塔分布的随机变量X～mixedbeta（a1，b1，a2，b2，p），其中p＝p1，1－p＝p2。显然，服从混合贝塔分布的随机变量也是在有限区间（0，1）内取值。

众所周知，为了保护投资者的权益，维持市场稳定，中国股票市场自1996年12月26日开始实施涨跌停板制度，规定除上市首日外，股票（含A、B股）、基金类证券在一个交易日内的交易价格相对于其开盘价格的涨跌幅度不得超过10%，超过涨跌限价的委托为无效委托。所以，中国股票日收益率（上市首日除外，以下同）的波动范围应该是在（－0．1，0．1）之间，并且，经线性变换xt＝（rt＋0．1）／0．2后，可将收益率rt映射到有限区间（0，1）上。另外，贝塔分布随着参数的不同表现出不同的形状。例如，当a、b＞1时，呈单峰分布，且若a≠b时，呈非对称分布。随着a和b的增大，分布的峰度增高。当0＜a，b＜1时，为U型分布，即取值在0或1附近的概率较大。于是，以一定概率将几个贝塔分布混合加权的混合贝塔分布能够较好地刻画取值于有限区间，具有高峰厚尾和非对称特征的随机变量。因此，本文认为假设股票收益率服从取值于有限区间内的随机分布无疑会更合理。

三、混合贝塔分布随机波动模型及其贝叶斯分析

为了讨论中国股票市场收益率的波动性，在股票收益率服从混合贝塔分布的假设下，本文构造了混合贝塔分布的SV模型，即SV－M模型，并提出了该模型的贝叶斯分析方法。

（一）SV－M模型

SV模型的一般形式为［10］：

其中rt为资产收益率，λt为收益率条件方差的对数形式，即λt＝log（var（rt｜It－1）），It－1为t－1期的信息集；γ为常数，表示平均波动水平，δ为反映波动率持续性的常数，vt为波动率的随机冲击，一般假设其服从独立同正态分布，均值为0，方差为σ2。ut为资产收益率的随机扰动项，ut的分布类型描述了收益率的分布类型，Taylor（1986）假设ut服从独立的标准正态分布，且与vt不相关，本文简记该模型为SV－N模型。

考虑到中国股票市场交易受10%涨跌停板制度的约束，本文假设波动率服从K＝2的混合贝塔分布，即ut～i．i．mixedbeta（a1，b1，a2，b2，p）。由于混合贝塔分布的取值区间为（0，1）区间，所以在建模之前，首先对收益率rt进行线性变换，为：

于是，基于混合贝塔分布建立的SV－M模型可以表示为：

其中xt为线性变换后的资产收益率。需要指出的是，因为混合贝塔分布的方差不再等于1，这时λt不再是收益率的对数条件方差。

由于K＝2的混合贝塔分布的密度函数为：

所以，在SV－M模型中，收益率的条件方差为var（rtIt－1）＝0．04×exp（λt）·var（ut），对 数形式为 log（var（rtIt－1））＝λt＋log（var（ut））＋log（0．04），因为var（ut）为常数，所以模型参数的意义不变，γ依然表示平均波动水平，δ反映波动率的持续性，vt为波动率的随机冲击。

为了同时满足模型形式的一致性和模型的可比较性，本文将SV－M模型依据以上变量关系进行变形，分别以收益率的线性变换xt和收益率的条件对数方差ht为被解释变量，建立如下模型：

（二）SV－M模型的贝叶斯分析

在SV－M模型中，不可观测变量为参数γ、δ、σ和隐性对数波动序列ht，可观测量为日收益率rt。

假设λ0服从均值为γ、方差为σ2的正态分布，于是，从SV－M的方差方程中可以看出，在给定ht－1和γ、δ、σ的条件下，ht服从均值为γ＋δ（γt－1－γ），方差为σ2的正态分布，即：

其中ht＝var（rt｜It－1）＝f（λt）。由于ht与λt之间存在等值函数关系，因此给定ht也就给定了λt，对于给定的λt，由随机波动模型的均值方程可以得到，x／exp（）服从混合贝塔分布，即：

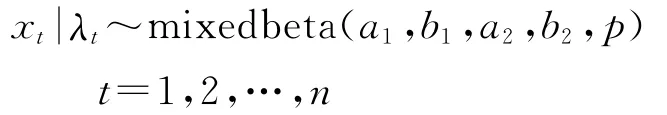
若用f（xt｜ht）表示xt关于ht的条件分布密度函数，则SV－M模型的似然函数为：

在贝叶斯分析中，参数先验分布的设置是贝叶斯统计分析的前提，根据Kim和Shephard等人的观点，对于参数γ、δ、σ和h0，本文选择的先验分布如下［11］：

γ～N（0，100），δ～Beta（20，1．5），σ2～IGa（2．5，0．025），h0～N（γ，σ2）

于是，参数γ、δ、σ的联合先验分布可以分解为三部分的乘积，即：

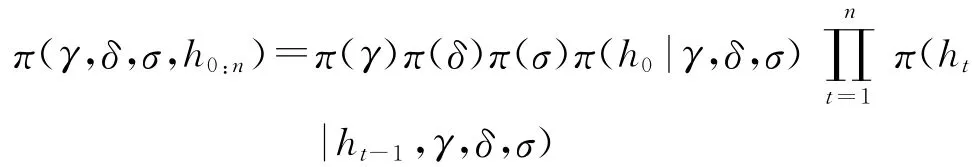
根据贝叶斯定理，不可观测量的联合后验密度分布与联合先验密度和模型的似然函数成正比，即：

π（γ，δ，σ，h0：n｜y0：n）∝L（y0：n｜γ，δ，σ，h0：n）π（γ，δ，σ，h0：n）

另外，在使用Gibbs抽样工具 WINBUGS时，以分布方差的倒数作为分布的精度，因此在编写程序时实际以1／σ2为参量的，令τ＝1／σ2，则τ～Gamma（2．5，0．025）。

为了实现Gibbs抽样，下面分别讨论各不可观测量的后验条件分布。

1．γ的后验条件分布。根据条件概率的定义，参数γ关于（δ，τ，h0：n）的后验条件分布密度函数为：

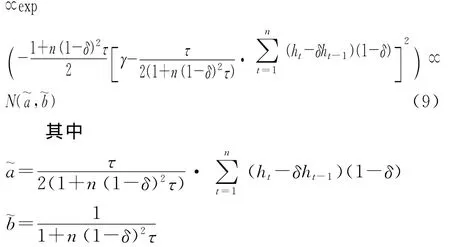
由于E（γ｜δ，τ，h0：n；y1：n）＝a～，所以参数γ 关于（δ，τ，h0：n）的贝叶斯条件估计为a～。

2．δ的后验条件分布。根据条件概率的定义，参数δ关于（γ，τ，h0：n）的后验条件分布密度函数为：

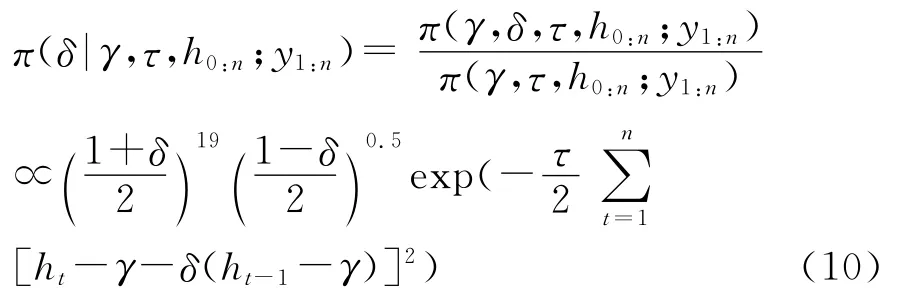
3．τ的后验条件分布。根据条件概率的定义，参数τ关于（γ，δ，h0：n）的后验条件分布密度函数为：

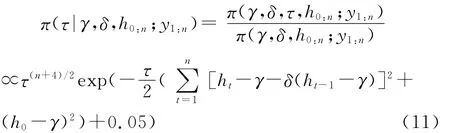
4．ht的后验条件分布。记h～t＝（h0，h1，…，ht－1，ht＋1，…，hn）′，t＝0，1，…，n，显然，h～t是一个n维向量。参数ht关于（γ，δ，τ，h～t）的后验条件密度函数为：

因此，基于SV－M模型各参数的后验条件分布即可采用Gibbs抽样算法得到参数联合后验分布的样本序列。限于篇幅，具体的抽样过程将结合下节的实证分析予以表述。

四、实证分析

（一）上证A股综指收益率的SV－M模型

本文以2008年1月2日至2011年12月30日的上证A股日综合指数的简单收益率数据为样本，数据来源于《大智慧证券分析系统》，样本容量为975个交易日。

经单位根检验，简单收益率为平稳序列，简单收益率序列和经线性变换xt＝（rt＋0．1）／0．2后收益率序列的描述性统计如表1所示。

表1 简单收益率rt、xt描述性统计表

由表1可见，与多数文献中所描述的一致，上证A股综指简单收益率序列也存在一定的左偏、峰度统计量大于3，并且JB统计量＝309．379 9＞χ0．01（2）＝9．210 3，即JB检验拒绝了上证A股综指简单收益率服从正态分布的零假定。另外，对于经线性变换后的序列xt＝（rt＋0．1）／0．2与上证 A 股综指简单收益率序列具有类似的统计特征。

为了使用贝叶斯方法估计SV－M模型的参数，本文利用 WINBUGS工具实现Gibbs抽样，其中选择了双链抽样的方法，以检验马尔科夫链的收敛性。从不同起始点出发，分别进行了10 000次Gibbs抽样。模拟收敛状态监测显示，当进行了1 000次抽样后，所有的参数都已经进入了收敛状态。为减少起始点初值的影响，本文对抽样数据进行退火，舍弃前5 000次抽样数据，选取后5 000次抽样，共计10 000个抽样进行参数估计。图1为后5 000次抽样双链轨迹，可以看出，双链交织为一、链行平稳，所以说明抽样收敛，即参数估计值稳定可靠。

图1 SV－M模型Gibbs抽样双链轨迹图

另外，参数后验均值和其他的一些统计量见表2。从表2可以看出，相对于后验均值，模拟参数的标准偏差sd和MC误差都相当的小。因此，MCMC后验均值估计的结果是相当精确的。

因此，本文根据上证A股日综指数据建立的混合贝塔分布的随机波动模型为：

（二）SV－M模型与SV－N模型的比较分析

为了比较基于混合贝塔分布的随机波动模型对样本数据的拟合程度，本文以相同的样本数据建立了基于正态分布的随机波动模型（SV－N模型），采用类似的MCMC抽样方法，SV－N模型参数的抽样轨迹图如图2所示，表3为参数后验均值等描述性统计量。

图2 SV－N模型Gibbs抽样双链轨迹图

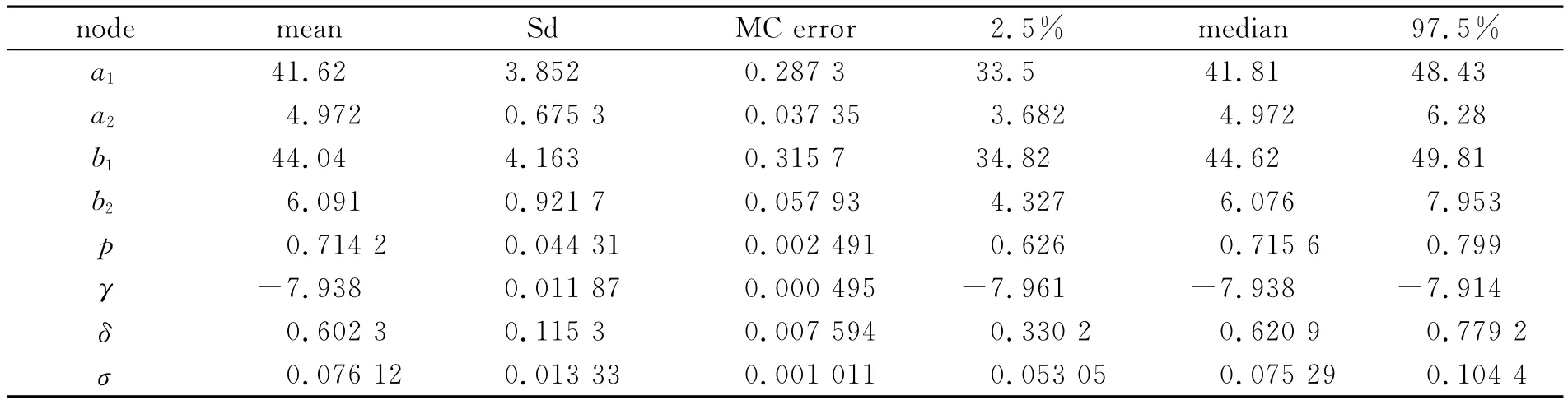
表2 SV－M参数估计结果表

表3 SV－N参数估计结果表

通过对表2和表3的比较分析，可以得到如下结论。

第一，表2中的SV－M模型的混合贝塔分布的参数a1＜b1、a2＜b2，体现出收益率序列左偏的特点，混合贝塔分布的峰度大于3，体现了中国的上证A股综指的收益率具有明显的尖峰厚尾的特性，表明上证A股综指收益率的分布明显地区别于正态分布。

第二，上证A股综指简单对数收益率在SV－N模型下的平均波动水平为－7．995，在SV－M模型下的平均波动水平为－7．938，经过指数变换后分别为0．000 337和0．000 356，都接近样本数据的真实方差0．000 384，说明两个模型都较好地反映了样本数据的生成过程，同时，SV－M模型的波动水平略高于SV－N模型，也更接近于样本数据的真实方差。SV－N模型和SV－M模型的波动持续性参数δ值分别为0．987 7和0．602 3，在一定程度上反映了上证A股综指简单收益率具有一定的波动持续性，但是两模型持续性系数相差较大，显然是源于采用了不同的分布。

由JB检验可见，上证A股综指简单收益率分布具有明显不同于正态分布的分布特征，其高峰厚尾和左偏的特征都从混合贝塔分布的拟合中得到了较好的体现。因此，用正态分布来拟合收益率数据，必然会低估样本数据的波动水平，并将高峰厚尾等分布特征归结为波动冲击，从而高估波动的持续性。从本文的估计结果可见，SV－N模型中的波动冲击服从均方差为0．120 7的正态分布，而SV－M模型中的波动冲击服从均方差为0．076 12的正态分布，SV－N模型的波动冲击明显高于SV－M模型。

另外，观察样本期内中国的证券市场，经历了2007—2008年的大牛市，股市持续低迷，从上证A股综指简单收益率的折线图中亦可以看出，前期处于牛市，波动强烈，后期处于低迷时期，波动微小，一方面体现了上证A股市场波动集群性的特点，另一方面也体现出波动的持续性并不高。因此，本文认为SV－M模型更真实地反映了样本数据的真实生成过程。

为了进一步比较SV－N模型和SV－M模型对样本数据的拟合程度，本文用MAE、MSE、RMSE三个度量指标作为评价标准，对两个模型进行比较评价。具体方法为：依据模型参数随机生成975个预测值＾rt；分别计算 MAE、MSE、RMSE；重复以上两个步骤1 000次，并计算三个指标的均值。

从表4和图3的SV－N模型与SV－M模型拟合度量结果中可以看出，SV－M模型比SV－N模型更好地拟合了样本数据的真实生成过程。

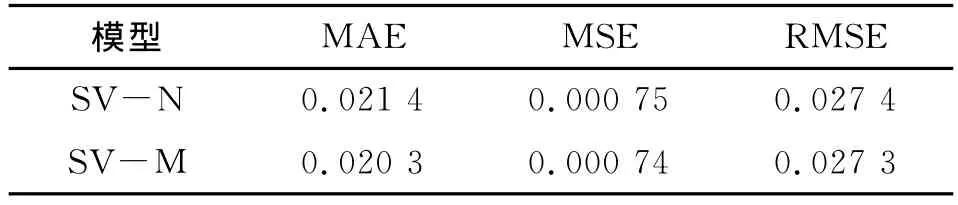
表4 SV－N模型与SV－M模型拟合度量结果比较表

图3 SV－N模型与SV－M模型对样本数据的拟合图

五、结 论

为了研究金融资产收益率的波动性，依据中国股票市场的涨跌停板交易制度的限制，本文建立了混合贝塔分布的随机波动模型，讨论了混合贝塔分布随机波动模型的贝叶斯分析方法，推导出了模型参数的后验条件分布密度函数，给出了混合贝塔分布随机波动模型贝叶斯分析的Gibbs抽样算法，并借助WINBUGS工具实现了混合贝塔分布随机波动模型的贝叶斯估计。

实证分析发现，混合贝塔分布的随机波动模型（SV－M）能够充分反映上证A股市场特点，较好地刻画了收益率高峰、厚尾和左偏的特征。通过与正态分布的随机波动模型的比较发现，SV－N模型低估了收益率的平均波动水平，高估了波动的持续性和波动的冲击扰动。

［1］ Jacquier E，Nicholas G P，Rossi P E．Bayesian Analysis of Stochastic Volatility Models with Fat-tails and Correlated Errors［J］．Journal of Econometrics，2004（2）．

［2］ Cappuccio N，Lubian D．MCMC Bayesian Estimation of a Skew-GED Stochastic Volatility Model［J］．Studies in Nonlinear Dynamics ＆ Econometrics，2004（8）．

［3］ Bovas A N Balakrishna，Ranjini S．Gamma Stochastic Volatility Models［J］．Journal of Forecasting，2006（3）．

［4］ Mike K P So，Li W K．A Threshold Stochastic Volatility Model［J］．Journal of Forcasting，2002（7）．

［5］ Bredit F J，N Cratoand P，deLima．The Detection and Estimation of Long Memory in Stochastic Volatility［J］．Journal of Econometrics，1998（83）．

［6］ Luis A，Gil－Alana，Juncal C，Fernando P D G．Stochastic Volatility in the Spanish Stock Market：A Long Memory Model with a Structural Break［J］．The European Journal of Finance，2008（1）．

［7］ 邱崇洋，刘继春，陈永娟．带ARMA（1，1）条件异方差相关的随机波动模型的 MCMC算法［J］．数学研究，2006（4）．

［8］ 周宏山，冀云．非对称随机波动模型在中国股市的应用［J］．统计与信息论坛，2007（4）．

［9］ 郝立亚，朱慧明，李素芳，曾惠芳．基于MCMC的贝叶斯长记忆随机波动模型的研究［J］．湖南大学学报：自然科学版，2011（1）．

［10］Taylor S J．Modeling Stochastic Volatility：A Review and Comparative Study［J］．Mathematical Finance，1994（4）．

［11］Kim S，Shephard N，Chib S．Stochastic Volatility：Likelihood Inference and Comparison with ARCH Models［J］．Review of Economic Studies，1998（3）．